Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T02:41:36.694Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial waves in a differentially rotating spherical shell

Published online by Cambridge University Press:  19 February 2013

C. Baruteau  and
M. Rieutord
C. Baruteau*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
M. Rieutord
Affiliation:
Institut de Recherche en Astrophysique et Planétologie, CNRS et Université de Toulouse, 14 avenue E. Belin, 31400 Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the properties of small-amplitude inertial waves propagating in a differentially rotating incompressible fluid contained in a spherical shell. For cylindrical and shellular rotation profiles and in the inviscid limit, inertial waves obey a second-order partial differential equation of mixed type. Two kinds of inertial modes therefore exist, depending on whether the hyperbolic domain where characteristics propagate covers the whole shell or not. The occurrence of these two kinds of inertial modes is examined, and we show that the range of frequencies at which inertial waves may propagate is broader than with solid-body rotation. Using high-resolution calculations based on a spectral method, we show that, as with solid-body rotation, singular modes with thin shear layers following short-period attractors still exist with differential rotation. They exist even in the case of a full sphere. 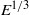In the limit of vanishing viscosities, the width of the shear layers seems to weakly depend on the global background shear, showing a scaling in ${E}^{1/ 3} $ with the Ekman number 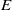$E$, as in the solid-body rotation case. There also exist modes with thin detached layers of width scaling with 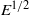${E}^{1/ 2} $ as Ekman boundary layers. The behaviour of inertial waves with a corotation resonance within the shell is also considered. For cylindrical rotation, waves get dramatically absorbed at corotation. In contrast, for shellular rotation, waves may cross a critical layer without visible absorption, and such modes can be unstable for small enough Ekman numbers.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 719 , 25 March 2013 , pp. 47 - 81
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barker, A. J. & Ogilvie, G. I. 2010 On internal wave breaking and tidal dissipation near the centre of a Solar-type star. Mon. Not. R. Astron. Soc. 404, 1849–1868.Google Scholar
Bryan, G. 1889 The waves on a rotating liquid spheroid of finite ellipticity. Phil. Trans. R. Soc. Lond. 180, 187–219.Google Scholar
Cartan, E. 1922 Sur les petites oscillations d’une masse fluide. Bull. Sci. Math. 46, 317–352; 356–369.Google Scholar
Dintrans, B., Rieutord, M. & Valdettaro, L. 1999 Gravito-inertial waves in a rotating stratified sphere or spherical shell. J. Fluid Mech. 398, 271–297.Google Scholar
Fricke, K. 1968 Instabilität stationärer Rotation in Sternen. ZAp 68, 317.Google Scholar
Friedlander, S. 1982 Turning surface behaviour for internal waves subject to general gravitational fields. Geophys. Astrophys. Fluid Dyn. 21, 189–200.Google Scholar
Friedlander, S. 1987 Hydromagnetic waves in the Earth’s fluid core. Geophys. Astrophys. Fluid Dyn. 39, 315–333.Google Scholar
Friedlander, S. & Siegmann, W. L. 1982 Internal waves in a rotating stratified fluid in an arbitrary gravitational field. Geophys. Astrophys. Fluid Dyn. 19, 267–291.Google Scholar
Goldreich, P. & Schubert, G. 1967 Differential rotation in stars. Astrophys. J. 150, 571.Google Scholar
Goodman, J. & Lackner, C. 2009 Dynamical tides in rotating planets and stars. ApJ 696, 2054–2067.Google Scholar
Greenspan, H. P. 1969 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hollerbach, R. & Kerswell, R. 1995 Oscillatory internal shear layers in rotating and precessing flows. J. Fluid Mech. 298, 327–339.CrossRefGoogle Scholar
Kelley, D., Triana, S. A., Zimmerman, D., Tilgner, A. & Lathrop, D. 2007 Inertial waves driven by differential rotation in a planetary geometry. Geophys. Astrophys. Fluid Dyn. 101, 469–487.Google Scholar
Kelley, D. H., Triana, S. A., Zimmerman, D. S. & Lathrop, D. P. 2010 Selection of inertial modes in spherical Couette flow. Phys. Rev. E 81 (2), 026311.Google Scholar
Kelvin, Lord 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155–168.Google Scholar
Kerswell, R. 1995 On the internal shear layers spawned by the critical regions in oscillatory Ekman boundary layers. J. Fluid Mech. 298, 311–325.Google Scholar
Latter, H. N. & Balbus, S. A. 2009 Inertial waves near corotation in three-dimensional hydrodynamical discs. Mon. Not. R. Astron. Soc. 399, 1058–1073.Google Scholar
Le Dizès, S. 2004 Viscous critical-layer analysis of vortex normal modes. Stud. Appl. Maths 112, 315–332.Google Scholar
Maas, L. & Lam, F.-P. 1995 Geometric focusing of internal waves. J. Fluid Mech. 300, 1–41.Google Scholar
Nelson, R. P., Gressel, O. & Umurhan, O. M. 2012 Linear and nonlinear evolution of the vertical shear instability in accretion discs. Mon. Not. R. Astron. Soc. arXiv:1209.2753.Google Scholar
Ogilvie, G. I. 2005 Wave attractors and the asymptotic dissipation rate of tidal disturbances. J. Fluid Mech. 543, 19–44.Google Scholar
Ogilvie, G. 2009 Tidal dissipation in rotating fluid bodies: a simplified model. Mon. Not. R. Astron. Soc. 396, 794–806.Google Scholar
Ogilvie, G. I. & Lin, D. N. C. 2004 Tidal dissipation in rotating giant planets. ApJ 610, 477–509.Google Scholar
Ogilvie, G. I. & Lin, D. N. C. 2007 Tidal dissipation in rotating solar-type stars. Astrophys. J. 661, 1180–1191.Google Scholar
Rieutord, M. 1987 Linear theory of rotating fluids using spherical harmonics part I: steady flows. Geophys. Astrophys. Fluid Dyn. 39, 163–182.Google Scholar
Rieutord, M. 2006 The dynamics of the radiative envelope of rapidly rotating stars. I. A spherical boussinesq model. A&A 451, 1025–1036.Google Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2001 Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144.Google Scholar
Rieutord, M., Triana, S. A., Zimmerman, D. S. & Lathrop, D. P. 2012 Excitation of inertial modes in an experimental spherical Couette flow. Phys. Rev. E 86 (2), 026304.Google Scholar
Rieutord, M. & Valdettaro, L. 1997 Inertial waves in a rotating spherical shell. J. Fluid Mech. 341, 77–99.Google Scholar
Rieutord, M. & Valdettaro, L. 2010 Viscous dissipation by tidally forced inertial modes in a rotating spherical shell. J. Fluid Mech. 643, 363–394.Google Scholar
Rieutord, M., Valdettaro, L. & Georgeot, B. 2002 Analysis of singular inertial modes in a spherical shell: the slender toroidal shell model. J. Fluid Mech. 463, 345–360.CrossRefGoogle Scholar
Stewartson, K. 1971 On trapped oscillations of a rotating fluid in a thin spherical shell. Tellus 23, 506–510.Google Scholar
Stewartson, K. 1972a On trapped oscillations of a rotating fluid in a thin spherical shell II. Tellus 24, 283–287.Google Scholar
Stewartson, K. 1972b On trapped oscillations in a slightly viscous rotating fluid. J. Fluid Mech. 54, 749–761.Google Scholar
Stewartson, K. & Rickard, J. 1969 Pathological oscillations of a rotating fluid. J. Fluid Mech. 35, 759–773.Google Scholar
Valdettaro, L., Rieutord, M., Braconnier, T. & Fraysse, V. 2007 Convergence and round-off errors in a two-dimensional eigenvalue problem using spectral methods and Arnoldi–Chebyshev algorithm. J. Comput. Appl. Math. 205, 382–393.Google Scholar
Wu, Y. 2005 Origin of tidal dissipation in Jupiter. II. The value of $Q$ . Astrophys. J. 635, 688–710.Google Scholar
Zahn, J.-P. 1992 Circulation and turbulence in rotating stars. A&A 265, 115.Google Scholar