Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T13:30:34.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Incompressible variable-density turbulence in an external acceleration field

Published online by Cambridge University Press:  24 August 2017

Ilana Gat Open the ORCID record for Ilana Gat [Opens in a new window] ,
Georgios Matheou ,
Daniel Chung Open the ORCID record for Daniel Chung [Opens in a new window]  and
Paul E. Dimotakis
Ilana Gat*
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
Georgios Matheou
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA Department of Mechanical Engineering, University of Connecticut, Storrs, CT 06269, USA
Daniel Chung
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Paul E. Dimotakis
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Dynamics and mixing of a variable-density turbulent flow subject to an externally imposed acceleration field in the zero-Mach-number limit are studied in a series of direct numerical simulations. The flow configuration studied consists of alternating slabs of high- and low-density fluid in a triply periodic domain. Density ratios in the range of 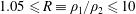$1.05\leqslant R\equiv \unicode[STIX]{x1D70C}_{1}/\unicode[STIX]{x1D70C}_{2}\leqslant 10$ are investigated. The flow produces temporally evolving shear layers. A perpendicular density–pressure gradient is maintained in the mean as the flow evolves, with multi-scale baroclinic torques generated in the turbulent flow that ensues. For all density ratios studied, the simulations attain Reynolds numbers at the beginning of the fully developed turbulence regime. An empirical relation for the convection velocity predicts the observed entrainment-ratio and dominant mixed-fluid composition statistics. Two mixing-layer temporal evolution regimes are identified: an initial diffusion-dominated regime with a growth rate 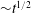${\sim}t^{1/2}$ followed by a turbulence-dominated regime with a growth rate 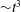${\sim}t^{3}$. In the turbulent regime, composition probability density functions within the shear layers exhibit a slightly tilted (‘non-marching’) hump, corresponding to the most probable mole fraction. The shear layers preferentially entrain low-density fluid by volume at all density ratios, which is reflected in the mixed-fluid composition.

JFM classification

Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulent Flows Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 827 , 25 September 2017 , pp. 506 - 535
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anuchina, N. N., Kucherenko, Y. A., Neuvazhaev, V. E., Ogibina, V. N., Shibarshov, L. I. & Yakovlev, V. G. 1978 Turbulent mixing at an accelerating interface between liquids of different density. Fluid Dyn. 13 (6), 916–920.CrossRefGoogle Scholar
Batchelor, G. K., Canuto, V. M. & Chasnov, J. R. 1992 Homogeneous buoyancy-generated turbulence. J. Fluid Mech. 235, 349–378.CrossRefGoogle Scholar
Bradshaw, P. 1977 Compressible turbulent shear layers. Annu. Rev. Fluid Mech. 9 (1), 33–52.CrossRefGoogle Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.Google Scholar
Brown, G. L. & Roshko, A. 2012 Turbulent shear layers and wakes. J. Turbul. 13, N51.Google Scholar
Chung, D.2009 Numerical simulation and subgrid-scale modeling of mixing and wall-bounded turbulent flows. PhD thesis, California Institute of Technology.Google Scholar
Chung, D. & Matheou, G. 2012 Direct numerical simulations of stationary homogeneous stratified sheared turbulence. J. Fluid Mech. 696, 434–467.Google Scholar
Chung, D. & Pullin, D. I. 2010 Direct numerical simulation and large-eddy simulation of stationary buoyancy-driven turbulence. J. Fluid Mech. 643, 279–308.Google Scholar
Cook, A. W. & Dimotakis, P. E. 2001 Transition stages of Rayleigh–Taylor instability between miscible fluids. J. Fluid Mech. 443, 69–99.CrossRefGoogle Scholar
Diamessis, P. J. & Nomura, K. K 2004 The structure and dynamics of overturns in stably stratified homogeneous turbulence. J. Fluid Mech. 499, 197–229.Google Scholar
Dimotakis, P. E. 1986 Two-dimensional shear-layer entrainment. AIAA J. 24, 1791–1796.Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.CrossRefGoogle Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37 (1), 329–356.Google Scholar
Donzis, D. A. & Yeung, P. K. 2010 Resolution effects and scaling in numerical simulations of passive scalar mixing in turbulence. Physica D 239, 1278–1287.Google Scholar
Gat, I., Matheou, G., Chung, D. & Dimotakis, P. E. 2016 Acceleration-driven variable-density turbulent flow. In Proceedings of the VIIIth International Symposium on Stratified Flows (ISSF), San Diego, CA. Retrieved from: http://escholarship.org/uc/item/61d722q6.Google Scholar
Gerz, T., Schumann, U. & Elghobashi, S. E. 1989 Direct numerical simulation of stratified homogeneous turbulent shear flows. J. Fluid Mech. 200, 563–594.Google Scholar
Gerz, T. & Yamazaki, H. 1993 Direct numerical simulation of buoyancy-driven turbulence in stably stratified fluid. J. Fluid Mech. 249, 415–440.Google Scholar
Hirschfelder, J. O., Curtiss, C. F. & Bird, R. B. 1964 Molecular Theory of Gases and Liquids. Wiley.Google Scholar
Ho, C. M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 16 (1), 365–422.Google Scholar
Holt, S. E, Koseff, J. R. & Ferziger, J. H. 1992 A numerical study of the evolution and structure of homogeneous stably stratified sheared turbulence. J. Fluid Mech. 237, 499–539.Google Scholar
Jacobitz, F. G., Sakar, S. & Van Atta, C. W. 1997 Direct numerical simulations of the turbulence evolution in a uniformly sheared and stably stratified flow. J. Fluid Mech. 342, 231–261.CrossRefGoogle Scholar
Kida, S. & Orszag, S. A. 1992 Energy and spectral dynamics in decaying compressible turbulence. J. Sci. Comput. 7 (1), 1–34.Google Scholar
Kolmogorov, A. N. 1941 Local structure of turbulence in an incompressible viscous fluid at very high Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Koochesfahani, M. M. & Dimotakis, P. E. 1986 Mixing and chemical reactions in a turbulent liquid mixing layer. J. Fluid Mech. 170, 83–112.Google Scholar
Livescu, D. 2013 Numerical simulations of two-fluid turbulent mixing at large density ratios and applications to the Rayleigh–Taylor instability. Phil. Trans. R. Soc. Lond. 371 (2003), 20120185.Google Scholar
Livescu, D. & Ristorcelli, J. R. 2007 Buoyancy-driven variable-density turbulence. J. Fluid Mech. 591, 43–71.Google Scholar
Livescu, D. & Ristorcelli, J. R. 2008 Variable-density mixing in buoyancy-driven turbulence. J. Fluid Mech. 605, 145–180.CrossRefGoogle Scholar
Livescu, D., Ristorcelli, J. R., Gore, R. A., Dean, S. H., Cabot, W. H. & Cook, A. W. 2009 High-Reynolds number Rayleigh–Taylor turbulence. J. Turbul. 10, N13.CrossRefGoogle Scholar
Mattner, T. W. 2011 Large-eddy simulations of turbulent mixing layers using the stretched-vortex model. J. Fluid Mech. 671, 507–534.Google Scholar
Métais, O. & Herring, J. R. 1989 Numerical simulations of freely evolving turbulence in stably stratified fluids. J. Fluid Mech. 202, 117–148.Google Scholar
Meyer, T. R., Dutton, J. C. & Lucht, R. P. 2006 Coherent structures and turbulent molecular mixing in gaseous planar shear layers. J. Fluid Mech. 558, 179–205.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.CrossRefGoogle Scholar
Pawlak, G. & Armi, L. 1998 Vortex dynamics in a spatially accelerating shear layer. J. Fluid Mech. 376, 1–35.Google Scholar
Rayleigh, Lord 1882 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. s1–14 (1), 170–177.Google Scholar
Read, K. I. 1984 Experimental investigation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12, 45–58.Google Scholar
Riley, J. J. & deBruynKops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15 (7), 2047–2059.Google Scholar
Rogers, M. M. & Moser, R. D. 1994 Direct simulation of a self-similar turbulent mixing layer. Phys. Fluids 6 (2), 903–923.Google Scholar
Sandoval, D. L.1995 The dynamics of variable-density turbulence. PhD thesis, University of Washington.Google Scholar
Shih, L. H., Koseff, J. R., Ferziger, J. H. & Rehmann, C. R. 2000 Scaling and parameterization of stratified homogeneous turbulent shear flow. J. Fluid Mech. 412, 1–20.Google Scholar
Slessor, M. D., Bond, C. L. & Dimotakis, P. E. 1998 Turbulent shear-layer mixing at high Reynolds numbers: effects of inflow conditions. J. Fluid Mech. 376, 115–138.Google Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96 (2), 297–324.Google Scholar
Staquet, C. & Godeferd, F. S. 1998 Statistical modelling and direct numerical simulations of decaying stably stratified turbulence. Part 1. Flow energetics. J. Fluid Mech. 360, 295–340.Google Scholar
Taylor, G. I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 201 (1065), 192–196.Google Scholar
Thorpe, S. A. 1968 A method of producing a shear flow in a stratified fluid. J. Fluid Mech. 32, 693–704.Google Scholar
Thorpe, S. A. 1978 On internal gravity waves in an accelerating shear flow. J. Fluid Mech. 88, 623–639.Google Scholar
Turner, J. S. 1979 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Youngs, D. L. 1984 Numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12, 32–44.Google Scholar
Youngs, D. L. 1989 Modelling turbulent mixing by Rayleigh–Taylor instability. Physica D 37, 270–287.Google Scholar