Hostname: page-component-6587cd75c8-vj8bv Total loading time: 0 Render date: 2025-04-24T09:05:34.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Impact of vaporization on drop aerobreakup

Published online by Cambridge University Press:  25 November 2024

B. Boyd ,
S. Becker  and
Y. Ling Open the ORCID record for Y. Ling [Opens in a new window]
B. Boyd*
Affiliation:
Department of Mechanical Engineering, University of Canterbury, Christchurch 8140, New Zealand
S. Becker
Affiliation:
Department of Mechanical Engineering, University of Canterbury, Christchurch 8140, New Zealand
Y. Ling*
Affiliation:
Department of Mechanical Engineering, University of South Carolina, Columbia, SC 29208, USA
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

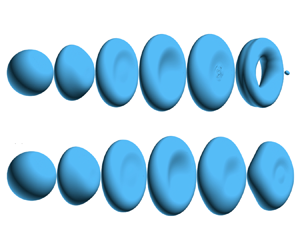
Aerodynamic breakup of vaporizing drops is commonly seen in many spray applications. While it is well known that vaporization can modulate interfacial instabilities, the impact of vaporization on drop aerobreakup is poorly understood. Detailed interface-resolved simulations were performed to systematically study the effect of vaporization, characterized by the Stefan number, on the drop breakup and acceleration for different Weber numbers and density ratios. It is observed that the resulting asymmetric vaporization rates and strengths of Stefan flow on the windward and leeward sides of the drop hinder bag development and prevent drop breakup. The critical Weber number thus generally increases with the Stefan number. The modulation of the boundary layer also contributes to a significant increase of drag coefficient. Numerical experiments were performed to affirm that the drop volume reduction plays a negligible role and the Stefan flow is the dominant reason for the breakup suppression and drag enhancement observed.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops Phase change: Condensation/evaporation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A33
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aalburg, C., Van Leer, B. & Faeth, G.M. 2003 Deformation and drag properties of round drops subjected to shock-wave disturbances. AIAA J. 41 (12), 2371–2378.CrossRefGoogle Scholar
Abramzon, B. & Sirignano, W.A. 1989 Droplet vaporization model for spray combustion calculations. Intl J. Heat Mass Transfer 32 (9), 1605–1618.CrossRefGoogle Scholar
Boyd, B., Becker, S. & Ling, Y. 2023 Simulation and modeling of the vaporization of a freely moving and deforming drop at low to moderate Weber numbers. Intl J. Heat Mass Transfer 218, 124735.CrossRefGoogle Scholar
Boyd, B. & Ling, Y. 2023 A consistent volume-of-fluid approach for direct numerical simulation of the aerodynamic breakup of a vaporizing drop. Comput. Fluids 254, 105807.CrossRefGoogle Scholar
Chirco, L., Maarek, J., Popinet, S. & Zaleski, S. 2022 Manifold death: a volume of fluid implementation of controlled topological changes in thin sheets by the signature method. J. Comput. Phys. 467, 111468.CrossRefGoogle Scholar
Flock, A.K., Guildenbecher, D.R., Chen, J., Sojka, P.E. & Bauer, H.-J. 2012 Experimental statistics of droplet trajectory and air flow during aerodynamic fragmentation of liquid drops. Intl J. Multiphase Flow 47, 37–49.CrossRefGoogle Scholar
Guildenbecher, D.R., López-Rivera, C. & Sojka, P.E. 2009 Secondary atomization. Exp. Fluids 46 (3), 371.CrossRefGoogle Scholar
Hsiang, L.-P. & Faeth, G.M. 1995 Drop deformation and breakup due to shock wave and steady disturbances. Intl J. Multiphase Flow 21, 545–560.CrossRefGoogle Scholar
Hsieh, D.Y. 1978 Interfacial stability with mass and heat transfer. Phys. Fluids 21, 745–748.CrossRefGoogle Scholar
Jackiw, I.M. & Ashgriz, N. 2021 On aerodynamic droplet breakup. J. Fluid Mech. 913, A33.CrossRefGoogle Scholar
Jain, M., Prakash, R.S., Tomar, G. & Ravikrishna, R.V. 2015 Secondary breakup of a drop at moderate Weber numbers. Proc. R. Soc. Lond. A 471 (2177), 20140930.Google Scholar
Jain, S.S., Tyagi, N., Prakash, R.S., Ravikrishna, R.V. & Tomar, G. 2019 Secondary breakup of drops at moderate Weber numbers: effect of density ratio and Reynolds number. Intl J. Multiphase Flow 117, 25–41.CrossRefGoogle Scholar
Ling, Y. & Mahmood, T. 2023 Detailed numerical investigation of the drop aerobreakup in the bag breakup regime. J. Fluid Mech. 972, A28.CrossRefGoogle Scholar
Marcotte, F. & Zaleski, S. 2019 Density contrast matters for drop fragmentation thresholds at low Ohnesorge number. Phys. Rev. Fluids 4 (10), 103604.CrossRefGoogle Scholar
Opfer, L., Roisman, I.V., Venzmer, J., Klostermann, M. & Tropea, C. 2014 Droplet–air collision dynamics: evolution of the film thickness. Phys. Rev. E 89, 013023.CrossRefGoogle ScholarPubMed
O'Rourke, P.J. & Amsden, A.A. 1987 The TAB method for numerical calculation of spray droplet breakup. Tech. Rep. LA-UR-2105. Los Alamos National Laboratory.CrossRefGoogle Scholar
Pillai, D.S. & Narayanan, R. 2018 Rayleigh–Taylor stability in an evaporating binary mixture. J. Fluid Mech. 848, R1.CrossRefGoogle Scholar
Ranger, A.A. & Nicholls, J.A. 1969 Aerodynamic shattering of liquid drops. AIAA J. 7, 285–290.Google Scholar
Renksizbulut, M. & Yuen, M.C. 1983 Experimental study of droplet evaporation in a high-temperature air stream. Trans. ASME J. Heat Transfer 105, 384–388.CrossRefGoogle Scholar
Rimbert, N., Castrillon Escobar, S., Meignen, R., Hadj-Achour, M. & Gradeck, M. 2020 Spheroidal droplet deformation, oscillation and breakup in uniform outer flow. J. Fluid Mech. 904, A15.CrossRefGoogle Scholar
Setiya, M. & Palmore, J.A. Jr 2023 Quasi-steady evaporation of deformable liquid fuel droplets. Intl J. Multiphase Flow 164, 104455.CrossRefGoogle Scholar
Strotos, G., Malgarinos, I., Nikolopoulos, N. & Gavaises, M. 2016 a Aerodynamic breakup of an n-decane droplet in a high temperature gas environment. Fuel 185, 370–380.CrossRefGoogle Scholar
Strotos, G., Malgarinos, I., Nikolopoulos, N. & Gavaises, M. 2016 b Numerical investigation of aerodynamic droplet breakup in a high temperature gas environment. Fuel 181, 450–462.CrossRefGoogle Scholar
Tang, K., Adcock, T. & Mostert, W. 2023 Bag film breakup of droplets in uniform airflows. J. Fluid Mech. 970, A9.CrossRefGoogle Scholar
Theofanous, T.G. 2011 Aerobreakup of Newtonian and viscoelastic liquids. Annu. Rev. Fluid Mech. 43, 661–690.CrossRefGoogle Scholar
Theofanous, T.G., Li, G.J. & Dinh, T.-N. 2004 Aerobreakup in rarefied supersonic gas flows. Trans. ASME J. Fluid Engng 126, 516–527.CrossRefGoogle Scholar
Tiwari, S.S., Pal, E., Bale, S., Minocha, N., Patwardhan, A.W., Nandakumar, K. & Joshi, J.B. 2020 Flow past a single stationary sphere, 2. Regime mapping and effect of external disturbances. Powder Technol. 365, 215–243.CrossRefGoogle Scholar
Zhang, B., Popinet, S. & Ling, Y. 2020 Modeling and detailed numerical simulation of the primary breakup of a gasoline surrogate jet under non-evaporative operating conditions. Intl J. Multiphase Flow 130, 103362.CrossRefGoogle Scholar