Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T01:19:32.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Impact of a shock wave on a heterogeneous foam film

Published online by Cambridge University Press:  10 December 2020

Quentin Raimbaud ,
Martin Monloubou ,
Steven Kerampran  and
Isabelle Cantat Open the ORCID record for Isabelle Cantat [Opens in a new window]
Quentin Raimbaud
Affiliation:
Université de Rennes, CNRS, IPR (Institut de Physique de Rennes) – UMR 6251, F-35000Rennes, France
Martin Monloubou
Affiliation:
ENSTA Bretagne, UMR CNRS 6027, Institut de Recherche Dupuy de Lôme – IRDL, F-29806Brest, France
Steven Kerampran
Affiliation:
ENSTA Bretagne, UMR CNRS 6027, Institut de Recherche Dupuy de Lôme – IRDL, F-29806Brest, France
Isabelle Cantat*
Affiliation:
Université de Rennes, CNRS, IPR (Institut de Physique de Rennes) – UMR 6251, F-35000Rennes, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

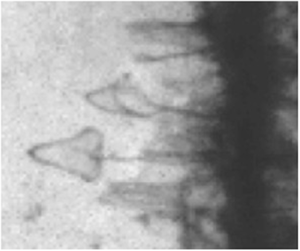
Liquid foams are, amongst other applications, used to mitigate shock waves. This aspect has received considerable attention at the macroscopic scale. However, the interaction between foam films and shock waves is still poorly understood and may be an important missing local information to build mitigation models. In this paper, we experimentally identify a new process leading to the foam film rupture, which dominates when the film thickness is sufficiently heterogeneous. Using a two-thickness film with a sharp and localised thickness gradient, we record the deformation of the interface between the thick and the thin parts. We observe the growth of an excess liquid area in the thin part and establish an analytical model and scaling laws which account for this phenomenon. Our results in this ideal configuration are consistent with actual rupture processes at stake in heterogeneous foam films.

JFM classification

Complex Fluids: Foams Compressible Flows: Shock waves Drops and Bubbles: Breakup/coalescence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 908 , 10 February 2021 , A27
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Borisov, A. A., Gel'fand, B. E., Kudinov, V. M., Palamarchuk, V. V., Stepanov, V. V., Timofeev, E. I. & Khomik, S. V. 1978 Shock waves in water foams. Acta Astronaut. 5, 1027–1033.CrossRefGoogle Scholar
Bremond, N. & Villermaux, E. 2005 Bursting thin liquid films. J. Fluid Mech. 524, 121–130.CrossRefGoogle Scholar
Britan, A., Ben-Dor, G., Shapiro, H., Liverts, M. & Shreiber, I. 2007 Drainage effects on shock wave propagating through aqueous foams. Colloids Surf. A 309, 5–23.CrossRefGoogle Scholar
Britan, A., Liverts, M. & Ben-Dor, G. 2009 Mitigation of sound waves by wet aqueous foams. Colloids Surf. A 344, 48–55.CrossRefGoogle Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.CrossRefGoogle Scholar
Courant, R. & Friedrichs, K. O. 1999 Flow and Shock Waves. Springer.Google Scholar
Culick, F. E. C. 1960 Comments on a ruptured soap film. J. Appl. Phys. 31, 1128.CrossRefGoogle Scholar
Del Prete, E., Chinnayya, A., Domergue, L., Hadjadj, A. & Haas, J.-F. 2013 Blast wave mitigation by dry aqueous foams. Shock Waves 23, 39–53.CrossRefGoogle Scholar
Goldfarb, I., Orenbakh, Z., Shreiber, I. & Vafina, F. 1997 Sound and weak shock wave propagation in gas-liquid foams. Shock Waves 7, 77–88.CrossRefGoogle Scholar
Goldfarb, I. I., Shreiber, I. R. & Vafina, F. I. 1992 Heat transfer effect on sound propagation in foam. J. Acoust. Soc. Am. 92, 2756–2769.CrossRefGoogle Scholar
Hartman, W. F., Boughton, B. A. & Larsen, M. E. 2006 Blast mitigation capabilities of aqueous foams. Tech. Rep. SAND2006-0533. Sandia National Laboratories.CrossRefGoogle Scholar
Henderson, L. F. 1989 On the refraction of shock waves. J. Fluid Mech. 198, 365–386.CrossRefGoogle Scholar
Kann, K. B. 2005 Sound waves in foams. Colloids Surf. A 263 (1), 315–319.CrossRefGoogle Scholar
Kann, K. B. & Kislitsyn, A. A. 2003 A film model of sound propagation in gas-liquid foams: 1. The sound velocity. Colloid J. 65, 26–30.CrossRefGoogle Scholar
Keller, J. B. 1983 Breaking of liquid films and threads. Phys. Fluids 26, 3451–3453.CrossRefGoogle Scholar
Keller, J. B. & Kolodner, I 1954 Instability of liquid surfaces and the formation of drops. J. Appl. Phys. 25, 918–921.CrossRefGoogle Scholar
de Krasinski, J. S. & Khosla, A. 1974 Shock wave propagation and attenuation in foams. In 5th Australian Conference. University of Canterbury.Google Scholar
Liang, Y., Liu, L., Zai, Z., Si, T. & Wen, C.-Y. 2020 Evolution of shock-acceleratred heavy gas layer. J. Fluid Mech. 886, A7.CrossRefGoogle Scholar
Liverts, M., Ram, O., Sadot, O., Apazidis, N. & Ben-Dor, G. 2015 Mitigation of exploding-wire-generated blast waves by aqueous foams. Phys. Fluids 27, 076103.CrossRefGoogle Scholar
Mujica, N. & Fauve, S. 2002 Sound velocity and absorption in a coarsening foam. Phys. Rev. E 66, 021404.CrossRefGoogle Scholar
Mysels, K. J., Shinoda, K. & Frankel, S. 1959 Soap Films: Study of their Thinning and a Bibliography. Pergamon.Google Scholar
Pierre, J., Dollet, B. & Leroy, V. 2014 Resonant acoustic propagation and negative density in liquid foams. Phys. Rev. Lett. 112, 148307.CrossRefGoogle ScholarPubMed
Ranjan, D., Anderson, M., Oakley, J. & Bonazza, R. 2005 Experimental investigation of a strongly shocked gas bubble. Phys. Rev. Lett. 94, 184507.CrossRefGoogle ScholarPubMed
Raspet, R. & Griffiths, S. K. 1983 The reduction of blast noise with aqueous foam. J. Acoust. Soc. Am. 74 (6), 1757–1763.CrossRefGoogle Scholar
Rayleigh, L. 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. R. Soc. Lond. A 14, 170–177.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.CrossRefGoogle Scholar
Shreiber, I., Ben-Dor, G., Britan, A. & Feklistov, V. 2006 Foam self-clarification phenomenon: an experimental investigation. Shock Waves 15, 199–204.CrossRefGoogle Scholar
Sloan, S. A. & Nettleton, M. A. 1975 A model for the axial decay of a shock wave in a large abrupt area change. J. Fluid Mech. 71 (4), 769–784.CrossRefGoogle Scholar
Taylor, G. I. 1950 The formation of a blast wave by a very intense explosion. I. Theoretical discussion. Proc. R. Soc. Lond. A 201, 159–174.Google Scholar
Taylor, G. I. 1959 The dynamics of thin sheets of fluid. III. Disintegration of fluid sheets. Proc. R. Soc. Lond. A 253 (1259), 313–321.Google Scholar
Velikovich, A. L., Wouchuk, J. G., Huete Ruiz de Lira, C., Metzler, N., Zalesak, S. & Schmitt, A. J. 2007 Shock front distortion and Richtmyer-Meshkov-type growth caused by a small preshock nonuniformity. Phys. Plasmas 14 (7), 072706.CrossRefGoogle Scholar