Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Porter, J.
Salgado Sánchez, P.
Shevtsova, V.
Yasnou, V.
Samoilova, Anna
and
Nepomnyashchy, Alexander
2021.
A review of fluid instabilities and control strategies with applications in microgravity.
Mathematical Modelling of Natural Phenomena,
Vol. 16,
Issue. ,
p.
24.
Martínez, N.
Salgado Sánchez, P.
Porter, J.
and
Ezquerro, J. M.
2021.
Effect of surface heat exchange on phase change materials melting with thermocapillary flow in microgravity.
Physics of Fluids,
Vol. 33,
Issue. 8,
Gaponenko, Y.
Yasnou, V.
Mialdun, A.
Nepomnyashchy, A.
and
Shevtsova, V.
2021.
Effect of the supporting disks shape on nonlinear flow dynamics in a liquid bridge.
Physics of Fluids,
Vol. 33,
Issue. 4,
Yano, Taishi
Mabuchi, Yuki
Yamaguchi, Makoto
and
Nishino, Koichi
2022.
Internal flow structure and dynamic free-surface deformation of oscillatory thermocapillary convection in a high-Prandtl-number liquid bridge.
Experiments in Fluids,
Vol. 63,
Issue. 6,
Kang, Qi
Wang, Jia
Duan, Li
Li, Xiang
Hu, Liang
Li, Lujun
Zhang, Shuoting
Wu, Di
Zhang, Pu
and
Hu, Wenrui
2022.
Transition to chaos of thermocapillary convection.
Physical Review E,
Vol. 106,
Issue. 3,
Boaro, Alessio
and
Lappa, Marcello
2022.
On the competition of transverse and longitudinal modes of Marangoni convection in a three-dimensional layer of viscoelastic fluid.
Physics of Fluids,
Vol. 34,
Issue. 12,
S̆eta, B.
Dubert, D.
Prats, M.
Gavalda, Jna.
Massons, J.
Bou-Ali, M.M.
Ruiz, X.
and
Shevtsova, V.
2022.
Transitions between nonlinear regimes in melting and liquid bridges in microgravity.
International Journal of Heat and Mass Transfer,
Vol. 193,
Issue. ,
p.
122984.
Stojanović, Mario
Romanò, Francesco
and
Kuhlmann, Hendrik C.
2022.
Stability of thermocapillary flow in liquid bridges fully coupled to the gas phase.
Journal of Fluid Mechanics,
Vol. 949,
Issue. ,
Lappa, Marcello
and
Waris, Wasim
2022.
On the role of heat source location and multiplicity in topographically controlled Marangoni–Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 939,
Issue. ,
Gaponenko, Y.
Yano, T.
Nishino, K.
Matsumoto, S.
and
Shevtsova, V.
2022.
Pattern selection for convective flow in a liquid bridge subjected to remote thermal action.
Physics of Fluids,
Vol. 34,
Issue. 9,
Varas, Roberto
Martínez, Úrsula
Olfe, Karl
Salgado Sánchez, Pablo
Porter, Jeff
and
Ezquerro, José Miguel
2023.
Effects of Thermocapillary and Natural Convection During the Melting of PCMs with a Liquid Bridge Geometry.
Microgravity Science and Technology,
Vol. 35,
Issue. 2,
Gaponenko, Y.
Yasnou, V.
Mialdun, A.
Bou-Ali, M. M.
Nepomnyashchy, A.
and
Shevtsova, V.
2023.
Variety of flow patterns in a liquid bridge subjected to a gas stream.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 381,
Issue. 2245,
Šeta, Berin
Dubert, Diana
Gavalda, Josefa
Massons, Jaume
Bou-Ali, Mounir M.
Ruiz, Xavier
and
Shevtsova, Valentina
2023.
Effect of heat transfer through an interface on convective melting dynamics of phase change materials.
Journal of Fluid Mechanics,
Vol. 966,
Issue. ,
Martínez Figueira, N.
Salgado Sánchez, P.
Bello, A.
Olfe, K.
and
Rodríguez, J.
2023.
Effect of surface heat exchange on phase change materials melting with thermocapillary flow in microgravity.
Physics of Fluids,
Vol. 35,
Issue. 8,
Stojanović, Mario
Romanò, Francesco
and
Kuhlmann, Hendrik C.
2024.
Flow instability in high-Prandtl-number liquid bridges with fully temperature-dependent thermophysical properties.
Journal of Fluid Mechanics,
Vol. 978,
Issue. ,
Stojanović, Mario
Romanò, Francesco
and
Kuhlmann, Hendrik C.
2024.
High-Prandtl-number thermocapillary liquid bridges with dynamically deformed interface: effect of an axial gas flow on the linear stability.
Journal of Fluid Mechanics,
Vol. 978,
Issue. ,
Stojanović, Mario
Romanò, Francesco
and
Kuhlmann, Hendrik C.
2024.
Instability of axisymmetric flow in thermocapillary liquid bridges: Kinetic and thermal energy budgets for two-phase flow with temperature-dependent material properties.
European Journal of Applied Mathematics,
Vol. 35,
Issue. 2,
p.
267.
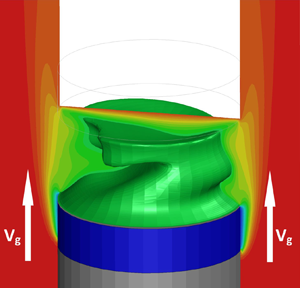
 $Pr=14$ with a gas flow parallel to the interface. The gas moves from the cold to the hot side with a constant velocity of
$Pr=14$ with a gas flow parallel to the interface. The gas moves from the cold to the hot side with a constant velocity of  $0.5\ \textrm {m}\ \textrm {s}^{-1}$ and its temperature is the main control parameter of the study. When the thermal stress
$0.5\ \textrm {m}\ \textrm {s}^{-1}$ and its temperature is the main control parameter of the study. When the thermal stress  ${\rm \Delta} T$ exceeds a critical value
${\rm \Delta} T$ exceeds a critical value  ${\rm \Delta} T_{cr}$, a three-dimensional oscillatory flow occurs in the system. A stability window of steady flow has been found to exist in the map of dynamical states in terms of gas temperature and applied thermal stress
${\rm \Delta} T_{cr}$, a three-dimensional oscillatory flow occurs in the system. A stability window of steady flow has been found to exist in the map of dynamical states in terms of gas temperature and applied thermal stress  ${\rm \Delta} T$. The study is carried out by tracking the evolution of hydrothermal waves with increasing gas temperature along three distinct paths with constant values of
${\rm \Delta} T$. The study is carried out by tracking the evolution of hydrothermal waves with increasing gas temperature along three distinct paths with constant values of  ${\rm \Delta} T$: path 1 is selected to be just above the threshold of instability while path 2 traverses the stability window and path 3 lies above it. We observe a variety of dynamics including standing and travelling waves, determine their dominant and secondary azimuthal wavenumbers, and suggest the mathematical equations describing hydrothermal waves. Multimodal standing waves, coexistence of travelling waves with several wavenumbers rotating in the same or opposite directions are among the most intriguing observations.
${\rm \Delta} T$: path 1 is selected to be just above the threshold of instability while path 2 traverses the stability window and path 3 lies above it. We observe a variety of dynamics including standing and travelling waves, determine their dominant and secondary azimuthal wavenumbers, and suggest the mathematical equations describing hydrothermal waves. Multimodal standing waves, coexistence of travelling waves with several wavenumbers rotating in the same or opposite directions are among the most intriguing observations.