Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-11T11:03:53.860Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydraulic jumps in a shallow flow down a slightly inclined substrate

Published online by Cambridge University Press:  30 September 2015

E. S. Benilov
E. S. Benilov*
Affiliation:
Department of Mathematics, University of Limerick, Ireland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

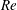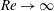This work examines free-surface flows down an inclined substrate. The slope of the free surface and that of the substrate are both assumed small, whereas the Reynolds number $Re$ remains unrestricted. A set of asymptotic equations is derived, which includes the lubrication and shallow-water approximations as limiting cases (as $Re\rightarrow 0$ and $Re\rightarrow \infty$, respectively). The set is used to examine hydraulic jumps (bores) in a two-dimensional flow down an inclined substrate. An existence criterion for steadily propagating bores is obtained for the 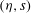$({\it\eta},s)$ parameter space, where 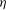${\it\eta}$ is the bore’s downstream-to-upstream depth ratio, and $s$ is a non-dimensional parameter characterising the substrate’s slope. The criterion reflects two different mechanisms restricting bores. If $s$ is sufficiently large, a ‘corner’ develops at the foot of the bore’s front – which, physically, causes overturning. If, in turn, 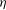${\it\eta}$ is sufficiently small (i.e. the bore’s relative amplitude is sufficiently large), the non-existence of bores is caused by a stagnation point emerging in the flow.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Waves/Free-surface Flows: Wave breaking
Type
Papers
Information
Journal of Fluid Mechanics , Volume 782 , 10 November 2015 , pp. 5 - 24
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benilov, E. S. 2014 A depth-averaged model for hydraulic jumps on an inclined substrate. Phys. Rev. E 89, 053013,1–6.Google Scholar
Benilov, E. S. & Lapin, V. N. 2011 Shock waves in Stokes flows down an inclined substrate. Phys. Rev. E 83, 06632.Google Scholar
Benilov, E. S. & Lapin, V. N. 2015 An example where lubrication theory comes short: hydraulic jumps in a flow down an inclined plate. J. Fluid Mech. 764, 277–295.Google Scholar
Benilov, E. S., Lapin, V. N. & O’Brien, S. B. G. 2012 On rimming flows with shocks. J. Engng Maths 75, 49–62.CrossRefGoogle Scholar
Benney, D. J. 1966 Long waves on liquid films. J. Math. Phys. 45, 150–155.CrossRefGoogle Scholar
Benney, D. J. 1973 Some properties of long nonlinear waves. Stud. Appl. Maths 52, 45–50.Google Scholar
Bertozzi, A. L. & Brenner, M. P. 1997 Linear stability and transient growth in driven contact lines. Phys. Fluids 9, 530–539.CrossRefGoogle Scholar
Bertozzi, A. L., Münch, A., Fanton, X. & Cazabat, A. M. 1998 Contact line stability and ‘undercompressive shocks’ in driven thin film flow. Phys. Rev. Lett. 81, 5169–5172.Google Scholar
Bertozzi, A. L., Münch, A., Shearer, M. & Zumbrun, K. 2001 Stability of compressive and undercompressive thin film travelling waves. Eur. J. Appl. Maths 12, 253–291.Google Scholar
Bertozzi, A. L. & Shearer, M. 2000 Existence of undercompressive travelling waves in thin film equations. SIAM J. Math. Anal. 33, 194–213.Google Scholar
Bohr, T., Putkaradze, V. & Watanabe, S. 1997 Averaging theory for the structure of hydraulic jumps and separation in laminar free-surface flows. Phys. Rev. Lett. 79, 1038–1041.Google Scholar
Chang, H.-C. & Demekhin, E. A. 2002 Complex Waves Dynamics on Thin Films. Elsevier.Google Scholar
Homsy, G. M. 1974 Model equations for wavy viscous film flow. Lect. Appl. Math. 15, 191–194.Google Scholar
Lin, S. P. 1974 Finite amplitude side-band stability of a viscous film. J. Fluid Mech. 63, 417–429.Google Scholar
Luchini, P. & Charru, F. 2010 Consistent section-averaged equations of quasi-one-dimensional laminar flow. J. Fluid. Mech. 656, 337–341.Google Scholar
Mavromoustaki, A., Matar, O. K. & Craster, R. V. 2010 Shock-wave solutions in two-layer channel flow. I. One-dimensional flows. Phys. Fluids 22, 112102.Google Scholar
Mei, C. C. 1966 Nonlinear gravity waves in a thin sheet of viscous fluid. J. Math. Phys. 45, 266–288.Google Scholar
Odulo, A. B. 1979 Long non-linear waves in the rotating ocean of variable depth. Dokl. Akad. Nauk SSSR 248, 1439–1442.Google Scholar
Rojas, N. O., Argentina, M., Cerda, E. & Tirapegui, E. 2010 Inertial lubrication theory. Phys. Rev. Lett. 104, 187801.CrossRefGoogle ScholarPubMed
Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. B 15, 357–369.Google Scholar
Ruyer-Quil, C. & Manneville, P. 2002 Further accuracy and convergence results on the modeling of flows down inclined planes by weighted-residual approximations. Phys. Fluids 14, 170–183.Google Scholar
Schlichting, H. 1979 Boundary-layer Theory. McGraw-Hill.Google Scholar
Weinstein, S. J. & Ruschak, K. J. 2004 Coating flows. Ann. Rev. Fluid Mech. 35, 29–53.CrossRefGoogle Scholar
Zakharov, V. E. 1981 On the Benney equations. Physica D 3, 193–202.Google Scholar