Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-20T00:50:57.619Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydraulic control of continuously stratified flow over an obstacle

Published online by Cambridge University Press:  18 April 2012

Kraig B. Winters  and
Laurence Armi
Kraig B. Winters*
Affiliation:
Scripps Institution of Oceanography and Mechanical and Aerospace Engineering, University of California San Diego, La Jolla, CA 92093, USA
Laurence Armi
Affiliation:
Scripps Institution of Oceanography and Mechanical and Aerospace Engineering, University of California San Diego, La Jolla, CA 92093, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

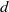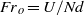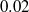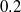Motivated by the laboratory experiments of Browand & Winant (Geophys. Fluid Dyn., vol. 4, 1972, pp. 29–53), a series of two-dimensional numerical simulations of flow past a cylinder of diameter are run for different values of the approach Froude number between and at 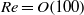. The observed flow is characterized by blocking and upstream influence in front of the cylinder and by relatively thin, fast jets over the top and bottom of the cylinder. This continuously stratified flow can be understood in terms of an inviscid non-diffusive integral inertia–buoyancy balance reminiscent of reduced-gravity single-layer hydraulics, but one where the reduced gravity is coupled to the thickness of the jets. The proposed theoretical framework describes the flow upstream of the obstacle and at its crest. The most important elements of the theory are the inclusion of upstream influence in the form of blocked flow within an energetically constrained depth range and the recognition that the flow well above and well below the active, accelerated layers is dynamically uncoupled. These constraints determine, through continuity, the transport in the accelerated layers. Combining these results with the observation that the flow is asymmetric around the cylinder, i.e. hydraulically controlled, allows us to determine the active layer thicknesses, the effective reduced gravity and thus all of the integral flow properties of the fast layers in good agreement with the numerically computed flows.

JFM classification

Geophysical and Geological Flows: Hydraulic control Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Topographic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 700 , 10 June 2012 , pp. 502 - 513
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Armi, L. 1989 Hydraulic control of zonal currents on a plane. J. Fluid. Mech. 201, 357–377.CrossRefGoogle Scholar
2. Baines, P. G. 1995 Topographic Effects in Stratified Flows. Cambridge University Press.Google Scholar
3. Browand, F. K. & Winant, C. D. 1972 Blocking ahead of a cylinder moving in a stratified fluid: an experiment. Geophys. Fluid Dyn. 4, 29–53.CrossRefGoogle Scholar
4. Castro, I. P. & Snyder, W. H. 1988 Upstream motions in stratified flow. J. Fluid Mech. 187, 487–506.CrossRefGoogle Scholar
5. Durran, D. R. & Klemp, J. B. 1987 Another look at downslope winds. Part II: Nonlinear amplification beneath wave overturning layers. J. Atmos. Sci. 44, 3402–3412.2.0.CO;2>CrossRefGoogle Scholar
6. Echeverri, P., Flynn, M. R., Winters, K. B. & Peacock, T. 2009 Low-mode internal tide generation: an experimental and numerical investigation. J. Fluid Mech. 638, 91–108.CrossRefGoogle Scholar
7. Graebel, W. P. 1969 On the slow motion of bodies in stratified and rotating fluids. Q. J. Mech. Appl. Maths 22, 39–54.Google Scholar
8. Hanazaki, H. 1989 Upstream advancing columnar disturbances in two-dimensional stratified flow of finite depth. Phys. Fluids A 1, 1976–1987.CrossRefGoogle Scholar
9. Long, R. R. 1955 Some aspects of the flow of stratified fluids. Tellus 7, 341–357.Google Scholar
10. Pratt, L. J. & Whitehead, J. A. 2008 Rotating Hydraulics: Nonlinear Topographic Effects in the Ocean and Atmosphere, p. 589. Springer.Google Scholar
11. Smith, R. B. 1985 On severe downslope winds. J. Atmos. Sci. 42, 2597–2603.2.0.CO;2>CrossRefGoogle Scholar
12. Winters, K., MacKinnon, J. & Mills, B. 2004 A spectral model for process studies of rotating, density-stratified flows. J. Atmos. Ocean Technol. 21, 69–94.2.0.CO;2>CrossRefGoogle Scholar
13. Wood, I. R. 1968 Selective withdrawal from a stably stratified fluid. J. Fluid. Mech. 32, 209–223.CrossRefGoogle Scholar