Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T19:43:27.817Z Has data issue: false hasContentIssue false
  • English
  • Français

Hybrid Eulerian–Lagrangian simulations for polymer–turbulence interactions

Published online by Cambridge University Press:  01 February 2013

Takeshi Watanabe  and
Toshiyuki Gotoh
Takeshi Watanabe*
Affiliation:
Graduate School of Engineering, Department of Scientific and Engineering Simulations, Nagoya Institute of Technology, Gokiso, Showa-ku, Nagoya 466-8555, Japan
Toshiyuki Gotoh
Affiliation:
Graduate School of Engineering, Department of Scientific and Engineering Simulations, Nagoya Institute of Technology, Gokiso, Showa-ku, Nagoya 466-8555, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

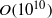The effects of polymer additives on decaying isotropic turbulence are numerically investigated using a hybrid approach consisting of Brownian dynamics simulations for an enormous number of dumbbells (of the order of 10 billion, $O(1{0}^{10} )$) and direct numerical simulations of turbulence making full use of large-scale parallel computations. Reduction of the energy dissipation rate and modification of the kinetic energy spectrum in the dissipation range scale were observed when the reaction term due to the polymer additives was incorporated into the equation of motion for the solvent fluid. An increase in the polymer concentration or Weissenberg number 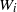${W}_{i} $ yielded significant modifications of the turbulence statistics at small scales, such as a suppression of the local energy dissipation fluctuations. A power-law decay of the kinetic energy spectrum 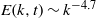$E(k, t)\sim {k}^{- 4. 7} $ was observed in the wavenumber range below the Kolmogorov length scale when 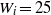${W}_{i} = 25$. The generation of intense vortices was suppressed by the polymer additives, consistent with previous studies using the constitutive equations. The field structures of the trace of the polymer stress depended on the intensity of its fluctuation: sheet-like structures were observed for the intermediate intensity region and filamentary structures were observed for the intense region. The results obtained with few polymers and large replicas could approximate those with many polymers and smaller replicas as far as the large-scale statistics were concerned.

JFM classification

Turbulent Flows: Isotropic turbulence Non-Newtonian Flows: Non-Newtonian Flows Non-Newtonian Flows: Polymers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , pp. 535 - 575
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afonso, M. M. & Vincenzi, D. 2005 Nonlinear elastic polymers in random flow. J. Fluid Mech. 540, 99–108.Google Scholar
Angelis, E. D. E., Casciola, C. M., Benzi, R. & Piva, R. 2005 Homogeneous isotropic turbulence in dilute polymers. J. Fluid Mech. 531, 1–10.Google Scholar
Arratia, P. E., Thomas, C. C., Diorio, J. & Gollub, J. P. 2006 Elastic instabilities of polymer solutions in cross-channel flow. Phys. Rev. Lett. 96, 144502.Google Scholar
Balkovsky, E., Fouxon, A. & Lebedev, V. 2000 Turbulent dynamics of polymer solutions. Phys. Rev. Lett. 84, 4765–4768.Google Scholar
Berti, S., Bistagnino, A., Boffetta, G., Celani, A. & Musacchio, S. 2006 Small-scale statistics of viscoelastic turbulence. Europhys. Lett. 76, 63–69.Google Scholar
Berti, S., Bistagnino, A., Boffetta, G., Celani, A. & Musacchio, S. 2008 Two-dimensional elastic turbulence. Phys. Rev. E 77, 055306.CrossRefGoogle ScholarPubMed
Bird, R. B., Curtiss, C. F., Amstrong, R. C. & Hassager, O. 1987 Dynamics of Polymetric Liquids, Vol. 2 Kinetic Theory, 2nd edn. Wiley.Google Scholar
Boffetta, G., Celani, A. & Mazzino, A. 2005 Drag reduction in the turbulent kolmogorov flow. Phys. Rev. E 71, 036307.Google Scholar
Boffetta, G., Celani, A. & Musacchio, S. 2003 Two-dimensional turbulence of dilute polymer solutions. Phys. Rev. Lett. 91, 034501.Google Scholar
Bosse, T., Kleiser, L. & Meiburg, E. 2006 Small particles in homogeneous turbulence: Setting velocity enhancement by two-way coupling. Phys. Fluids 18, 027102.Google Scholar
Brethouwer, G., Hunt, J. C. R. & Nieuwstadt, F. T. M. 2003 Micro-structure and Lagrangian statistics of the scalar field with a mean gradient in isotropic turbulence. J. Fluid Mech. 474, 193–225.Google Scholar
Burghelea, T., Segre, E. & Steinberg, V. 2004 Mixing by polymers: Experimental test of decay regime of mixing. Phys. Rev. Lett. 92, 164501.Google Scholar
Burghelea, T., Segre, E. & Steinberg, V. 2006 Role of elastic stress in statistical and scaling properties of elastic turbulence. Phys. Rev. Lett. 96, 214502.Google Scholar
Burghelea, T., Segre, E. & Steinberg, V. 2007 Elastic turbulence in von Karman swirling flow between two disk. Phys. Fluids 19, 053104.Google Scholar
Cai, W.-H., Li, D.-C. & Zhang, H.-N. 2010 Dns study of decaying homogeneous isotropic turbulence with polymer additives. J. Fluid Mech. 665, 334–356.Google Scholar
Celani, A., Musacchio, S. & Vincenzi, D. 2005a Polymer transport in random flow. J. Stat. Phys. 118, 531–554.Google Scholar
Celani, A., Puliafito, A. & Turitsyn, K. 2005b Polymers in linear shear flow: a numerical study. Europhys. Lett. 70, 464–470.Google Scholar
Chertkov, M. 2000 Polymer stretching by turbulence. Phys. Rev. Lett. 84, 4761–4764.CrossRefGoogle ScholarPubMed
Chertkov, M., Kolokolov, I., Lebedev, V. & Turitsyn, K. 2005 Polymer statistics in a random flow with mean shear. J. Fluid Mech. 531, 251–260.Google Scholar
Choi, H. J., Lim, S. T., Lai, Pik-Yin & Chan, C. K. 2002 Turbulent drag reduction and degradation of DNA. Phys. Rev. Lett. 89, 088302.Google Scholar
Crawford, A. M., Mordant, N., Xu, H. & Bodenschatz, E. 2008 Fluid acceleration in the bulk of turbulent dilute polymer solutions. New J. Phys. 10, 123015.Google Scholar
Davoudi, J. & Schumacher, J. 2006 Stretching of polymers around the Kolmogorov scale in a turbulent shear flow. Phys. Fluids 18, 025103.Google Scholar
De Gennes, P. G. 1974 Coil–stretch transition of dilute flexible polymers under ultrahigh velocity gradients. J. Chem. Phys. 60, 5030–5042.Google Scholar
Doi, M. & Edwards, S. F. 1986 The Theory of Polymer Dynamics. Oxford University Press.Google Scholar
Eckhardt, B., Kronjager, J. & Schumacher, J. 2002 Stretching of polymers in a turbulent enviroment. Comput. Phys. Commun. 147, 538–543.Google Scholar
Elbing, B. R., Dowling, D. R., Perlin, M. & Ceccio, S. L. 2010 Diffusion of drag-reducing polymer solutions within a rough-walled turbulent boundary layer. Phys. Fluids 22, 045102.Google Scholar
Fouxon, A. & Lebedev, V. 2003 Spectra of turbulence in dilute polymer solutions. Phys. Fluids 15, 2060–2073.Google Scholar
Fouxon, I. & Posch, H. A. 2012 Dynamics of threads and polymers in turbulence: power-law distributions and synchronization. J. Stat. Mech. P01022.Google Scholar
Frisch, U. 1995 Turbulence. Cambridge University Press.Google Scholar
Fukayama, D., Oyamada, T., Nakano, T., Gotoh, T. & Yamamoto, K. 2000 Longitudinal structure functions in decaying and forced turbulence. J. Phys. Soc. Japan 69, 701–715.Google Scholar
Gerashchenko, S., Chevallard, C. & Steinberg, V. 2005 Single-polymer dynamics: coil–stretch transition in a random flow. Europhys. Lett. 71, 221–227.Google Scholar
Gerashchenko, S. & Steinberg, V. 2006 Statistics of tumbling of a single polymer molecule in shear flow. Phys. Rev. Lett. 96, 038304.Google Scholar
Gillissen, J. J. J. 2008 Polymer flexibility and turbulent drag reduction. Phys. Rev. E 78, 046311.Google Scholar
Gotoh, T. & Watanabe, T. 2012 Scalar flux in a uniform mean scalar gradient in homogeneous isotropic steady turbulence. Physica D 241, 141–148.Google Scholar
Gotoh, T., Watanabe, Y., Shiga, Y., Nakano, T. & Suzuki, E. 2007 Statistical properties of four-dimensional turbulence. Phys. Rev. E 75, 016310.Google Scholar
Groisman, A. & Steinberg, V. 2000 Elastic turbulence in a polymer solution flow. Nature 405, 53–55.Google Scholar
Groisman, A. & Steinberg, V. 2001 Efficient mixing at low Reynolds numbers using polymer additives. Nature 410, 905–908.Google Scholar
Jin, S. & Collins, L. R. 2007 Dynamics of dissolved polymer chains in isotropic turbulence. New J. Phys. 9, 360.Google Scholar
Jun, Y. & Steinberg, V. 2009 Power and pressure fluctuations in elastic turbulence over a wide range of polymer concentrations. Phys. Rev. Lett. 102, 124503.Google Scholar
Laso, M. & Ottinger, H. C. 1993 Calculation of viscoelastic flow using molecular models: the Connffessit approach. J. Non-Newtonian Fluid Mech. 47, 1–20.Google Scholar
Liberzon, A., Guala, M., Kinzelbach, W. & Tsinober, A. 2006 On turbulent kinetic energy production and dissipation in dilute polymer solutions. Phys. Fluids 18, 125101.CrossRefGoogle Scholar
Liberzon, A., Guala, M., Lüthi, B., Kinzelbach, W. & Tsinober, A. 2005 Turbulence in dilute polymer solutions. Phys. Fluids 17, 031707.Google Scholar
Liu, Y. & Steinberg, V. 2010 Stretching of polymer in a random flow: effect of a shear rate. Europhys. Lett. 90, 44005.Google Scholar
Lumley, J. L. 1973 Drag reduction in turbulent flow by polymer additives. J. Polym. Sci.: Macromol. Rev. 7, 263–290.Google Scholar
McComb, W. D., Allan, J. & Greated, C. A. 1977 Effect of polymer additives on the small-scale structure of grid-generated turbulence. Phys. Fluids 20, 873–879.Google Scholar
Ouellette, N. T., Xu, H. & Bodenschatz, E. 2009 Bulk turbulence in dilute polymer solutions. J. Fluid Mech. 629, 375–385.Google Scholar
Perlekar, P., Mitra, D. & Pandit, R. 2006 Manifestations of drag reduction by polmer additives in decaying, homogeneous, isotropic turbulence. Phys. Rev. Lett. 97, 264501.CrossRefGoogle Scholar
Perlekar, P., Mitra, D. & Pandit, R. 2010 Direct numerical simulations of statistically steady, homobeneous, isotropic turbulence with polymer additives. Phys. Rev. E 82, 066313.CrossRefGoogle ScholarPubMed
Peters, T. & Schumacher, J. 2007 Two-way coupling of finitely extensible nonlinear elastic dumbbells with a turbulent shear flow. Phys. Fluids 19, 065109.Google Scholar
Proccacia, I., L’vov, V. S. & Benzi, R. 2008 Theory of drag reduction by polymers in wall-bounded turbulence. Rev. Mod. Phys. 80, 225–247.Google Scholar
Prosperetti, A. & Tryggvason, G. 2007 Computational Methods for Multiphase Flow (ed. Prosperetti, A. & Tryggvason, G.). Cambridge University Press.Google Scholar
Schumacher, J., Sreenivasan, K. R. & Yeung, P. K. 2005 Very fine structures in scalar mixing. J. Fluid Mech. 531, 113–122.Google Scholar
Sreenivasan, K. R. & White, C. M. 2000 The onset of drag reduction by dilute polymer additives, and the maximum drag reduction asymptote. J. Fluid Mech. 409, 149–164.Google Scholar
Stone, P. A. & Graham, D. 2003 Polymer dynamics in a model of the turbulent buffer layer. Phys. Fluids 15, 1247–1256.Google Scholar
Sureshkumar, R., Beris, A. N. & Handler, R. A. 1997 Direct numerical simulation of the turbulent channel flow of a polymer solution. Phys. Fluids 9, 743–755.Google Scholar
Tamano, S., Itoh, M., Hotta, S., Yokota, K. & Morinishi, Y. 2009 Effect of rheorogical properties on drag reduction in turbulent boundary layer flow. Phys. Fluids 21, 055101.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.Google Scholar
Terrapon, V. E., Dubief, Y., Moin, P., Shaqfeh, E. S. G. & Lele, S. K. 2004 Simulated polymer stretch in a turbulent flow using brownian dynamics. J. Fluid Mech. 504, 61–71.Google Scholar
Thiffeault, J-L. 2003 Finite extension of polymers in turbulent flow. Phys. Lett. A 308, 445–450.Google Scholar
Vaithianathan, T. & Collins, L. R. 2003 Numerical approach to simulating turbulent flow of a viscoelastic polymer solution. J. Comput. Phys. 187, 1–21.Google Scholar
van Doorn, E., White, C. M. & Sreenivasan, K. R. 1999 The decay of grid turbulence in polymer and surfactant solutions. Phys. Fluids 11, 2387–2393.Google Scholar
Watanabe, T. & Gotoh, T. 2007 Inertial range intermittency and accuracy of direct numerical simulation of turbulence and passive scalar turbulence. J. Fluid Mech. 590, 117–146.Google Scholar
Watanabe, T. & Gotoh, T. 2010 Coil–stretch transition in an ensemble of polymers in isotropic turbulence. Phys. Rev. E 81, 066301.Google Scholar
Yasuda, S. & Yamamoto, R. 2010 Multiscale modelling and simulation for polymer melt flows between parallel plate. Phys. Rev. E 81, 036308.Google Scholar
Yeung, P. K. & Pope, S. B. 1988 An algorithm for tracking fluid particles in numerical simulations of homogeneous turbulence. J. Comput. Phys 79, 373–416.Google Scholar