Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T08:27:34.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Highly separated axisymmetric step shock-wave/turbulent-boundary-layer interaction

Published online by Cambridge University Press:  06 September 2017

Gaurav Chandola ,
Xin Huang  and
David Estruch-Samper Open the ORCID record for David Estruch-Samper [Opens in a new window]
Gaurav Chandola
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 117575, Singapore
Xin Huang
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 117575, Singapore
David Estruch-Samper*
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 117575, Singapore
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The unsteadiness of a shock-wave/turbulent-boundary-layer interaction induced by an axisymmetric step (cylinder/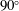$90^{\circ }$-disk) is investigated experimentally at Mach 3.9. A large-scale separation of the order of previously reported incoming turbulent superstructures is induced ahead of the step 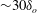${\sim}30\unicode[STIX]{x1D6FF}_{o}$ and followed by a downstream separation of 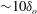${\sim}10\unicode[STIX]{x1D6FF}_{o}$ behind it, where 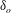$\unicode[STIX]{x1D6FF}_{o}$ is the incoming boundary-layer thickness. Narrowband high-frequency instabilities shift gradually to more moderate frequencies along the upstream separation region exhibiting a strong predominance of shear-induced disturbance levels – arising between the outer high-speed flow and the subsonic bubble. Through spectral/time-resolved analysis of this high Reynolds number and large-scale separation, results offer new insights into the shear layer’s inception and evolution (convection, growth and instability) and its influence on interaction unsteadiness.

JFM classification

Boundary Layers: Boundary layer separation Aerodynamics: High-speed flow Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , pp. 236 - 270
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. S. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–53.Google Scholar
Agostini, L., Larchevêque, L. & Dupont, P. 2015 Mechanism of shock unsteadiness in separated shock/boundary-layer interactions. Phys. Fluids 27, 126103.Google Scholar
Babinsky, H. & Harvey, J. K.(Eds) 2011 Shock Wave–Boundary-Layer Interactions, Cambridge Aerospace Series, No. 32. Cambridge University Press.Google Scholar
Baldwin, B. S. & Lomax, H.1978 Thin layer approximation and algebraic model for separated turbulent flows. In 16th Aerospace Sciences Meeting, Huntsville, USA. AIAA Paper 78-257.Google Scholar
Beresh, S., Henfling, J., Spillers, R. & Pruett, B. 2011 Fluctuating wall pressures measured beneath a supersonic turbulent boundary layer. Phys. Fluids 23, 075110.Google Scholar
Casper, K. M., Beresh, S. J. & Schneider, S. P. 2014 Pressure fluctuations beneath instability wavepackets and turbulent spots in a hypersonic boundary layer. J. Fluid Mech. 756, 1058–1091.Google Scholar
Cherry, N. J., Hillier, R. & Latour, M. E. M. 1984 Unsteady measurements in a separated and reattaching flow. J. Fluid Mech. 144, 13–46.Google Scholar
Chong, M. S., Soria, J., Perry, A. E., Chacin, J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.Google Scholar
Clemens, N. T. & Narayanaswamy, V.2009 Shock/turbulent boundary layer interactions: review of recent work on sources of unsteadiness. AIAA 2009–3710.Google Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.Google Scholar
Corcos, G. M. 1963 Resolution of pressure in turbulence. J. Acoust. Soc. Am. 35 (2), 192–199.Google Scholar
Duan, L., Choudhari, M. & Zhang, C. 2016 Pressure fluctuations induced by a hypersonic turbulent boundary layer. J. Fluid Mech. 804, 578–607.Google Scholar
Dupont, P., Haddad, C. & Debiève, J. F. 2006 Space and time organization in a shock-induced separated boundary layer. J. Fluid Mech. 559, 255–277.Google Scholar
Eaton, J. K. & Johnston, J. P. 1981 A review of research on subsonic turbulent flow reattachment. AIAA J. 19 (9), 1093–1100.Google Scholar
Estruch-Samper, D., Macmanus, D., Richardson, D., Lawson, N., Garry, K. & Stollery, J. 2010 Experimental study of unsteadiness in supersonic shock-wave/turbulent boundary-layer interactions with separation. Aeronaut. J. 114, 299–308.Google Scholar
Estruch-Samper, D. 2016 Reattachment heating upstream of short compression ramps in hypersonic flow. Exp. Fluids 57 (5), 1–17.Google Scholar
Ganapathisubramani, B., Clemens, N. & Dolling, D. 2007 Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585, 369–394.Google Scholar
Humble, R. A., Scarano, F. & van Oudheusden, B. W. 2009 Unsteady aspects of an incident shock wave/turbulent boundary layer interaction. J. Fluid Mech. 635, 47–74.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.Google Scholar
Kiya, M. & Sasaki, K. 1983 Structure of a turbulent separation bubble. J. Fluid Mech. 137, 83–113.Google Scholar
Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward facing step. J. Fluid Mech. 330, 349–374.Google Scholar
Murray, N., Hillier, R. & Williams, S. 2013 Experimental investigation of axisymmetric hypersonic shock-wave/turbulent-boundary-layer interactions. J. Fluid Mech. 714, 152–189.Google Scholar
Na, Y. & Moin, P. 1998 Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 374, 379–405.CrossRefGoogle Scholar
Naguib, A. M., Gravante, S. P. & Wark, C. E. 1996 Extraction of turbulent wall-pressure time-series using an optimal filtering scheme. Exp. Fluids 22 (1), 14–22.CrossRefGoogle Scholar
Papamoschou, D. & Roshko, A. 1988 The compressible turbulent shear layer: an experimental study. J. Fluid Mech. 197, 453–477.Google Scholar
Piponniau, S., Dussauge, J. P., Debiève, J. F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.Google Scholar
Priebe, S. & Martin, M. P. 2012 Low-frequency unsteadiness in shock wave turbulent boundary layer interaction. J. Fluid Mech. 699, 1–49.CrossRefGoogle Scholar
Silveira Neto, A., Grand, D., Metais, O. & Lesieur, M. 1993 A numerical investigation of the coherent vortices in turbulence behind a backward-facing step. J. Fluid Mech. 256, 1–25.Google Scholar
Souverein, L. J., Dupont, P., Debiève, J. F., Dussauge, J. P., van Oudheusden, B. W. & Scarano, F. 2009 Effect of interaction strength on the unsteady behaviour of shock wave boundary layer interactions. In 39th AIAA Fluid Dyn. Conf. AIAA Paper 2009-3715.Google Scholar
Souverein, L. J., Dupont, P., Debiève, J. F., Dussauge, J. P., Van Oudheusden, B. W. & Scarano, F. 2010 Effect of interaction strength on unsteadiness in turbulent shock-wave-induced separations. AIAA J. 48 (7), 1480–1493.Google Scholar
Thomas, F. O., Putman, C. M. & Chu, H. C. 1994 On the mechanism of unsteady shock oscillation in shock wave/turbulent boundary layer interaction. Exp. Fluids 18, 69–81.Google Scholar
Touber, E. & Sandham, N. D. 2011 Low-order stochastic modelling of low-frequency motions in reflected shock-wave/boundary-layer interactions. J. Fluid Mech. 671, 417–465.Google Scholar
Wu, M. & Martin, M. P. 2008 Analysis of shock motion in shockwave and turbulent boundary layer interaction using direct numerical simulation data. J. Fluid Mech. 594, 71–83.Google Scholar

Chandola et al. supplementary movie 1

High-speed schlieren corresponding to figure 7b and played at a rate of: t/To=1 (top), t/To=10 (bottom left) and t/To=100 (bottom right) per second in the video, where To is the characteristic timescale of upstream bubble pulsations. For h/δo=5.9 step at Me=3.9 and Ree= 6.1x107m-1(fo= 391 Hz). White square indicates region of interest considered in movie 2.

Download Chandola et al. supplementary movie 1(Video)
Video 123.6 MB

Chandola et al. supplementary movie 2

Highly separated axisymmetric step STBLI (left) with schlieren-based correlation between upstream separation shock displacement xson the top φ=0o and bottom of the image φ=180o (top right) and variation of respective shock displacement ΔxU* with time, where ΔxU*=(xs−xs,av)/L (bottom right). Played consecutively at (a) t/To=1, (b) t/To=10 and (c) t/To=100 per second in the video, with correlation plot populated with time. Joint probability density function (PDF) contour levels are shown at the end, with poor correlation at low frequencies between opposite sides (1kHz low-pass filter). Note: total test window duration of 5.24s covers an equivalent of 2050To (Ue/δo=0.94x106).

Download Chandola et al. supplementary movie 2(Video)
Video 63.9 MB