Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Leite, Paulo H.
and
Santos, Wilson F.
2013.
Computational Analysis of Low-Density Hypersonic Flow over Backward-Facing Steps.
Prakash, Ram
Gai, Sudhir L.
and
O'Byrne, Sean
2015.
Numerical Study of Hypersonic Separated Flow over an Expansion-Compression Surface.
khraibut, amna
Gai, Sudhir
and
Neely, Andrew J.
2015.
Numerical Investigation of Bluntness Effects on Hypersonic Leading Edge Separation.
Deepak, N. R.
Gai, S. L.
O’ Byrne, Sean
and
Moss, J. N.
2015.
29th International Symposium on Shock Waves 1.
p.
521.
Park, Gisu
Park, Chul
Jin, Yuin
Choi, Hojin
Byun, Jongryul
and
Hwang, Kiyoung
2015.
Ethylene Transverse Jets in Supersonic Crossflows.
Journal of Propulsion and Power,
Vol. 31,
Issue. 3,
p.
773.
Park, Gisu
Gai, Sudhir L.
and
Neely, Andrew J.
2016.
Base Flow of Circular Cylinder at Hypersonic Speeds.
AIAA Journal,
Vol. 54,
Issue. 2,
p.
458.
Prakash, Ram
Gai, Sudhir L.
and
O'Byrne, Sean B.
2017.
DSMC Computations of Separation over a `Tick' model in Hypersonic High Enthalpy Transitional Flows.
Prakash, R.
Gai, S.
and
O’Byrne, S.
2018.
A direct simulation Monte Carlo study of hypersonic leading-edge separation with rarefaction effects.
Physics of Fluids,
Vol. 30,
Issue. 6,
Estruch-Samper, David
and
Chandola, Gaurav
2018.
Separated shear layer effect on shock-wave/turbulent-boundary-layer interaction unsteadiness.
Journal of Fluid Mechanics,
Vol. 848,
Issue. ,
p.
154.
Le Page, Laurent M.
Barrett, Matthew
O’Byrne, Sean
and
Gai, Sudhir L.
2019.
Rotational temperature imaging of a leading-edge separation in hypervelocity flow.
Vol. 2132,
Issue. ,
p.
110001.
Lee, Sungmin
Song, Hakyoon
and
Park, Gisu
2020.
Study of strut interference in high-speed flows.
Experiments in Fluids,
Vol. 61,
Issue. 4,
Le Page, Laurent M.
Barrett, Matthew
O’Byrne, Sean
and
Gai, Sudhir L.
2020.
Laser-induced fluorescence velocimetry for a hypersonic leading-edge separation.
Physics of Fluids,
Vol. 32,
Issue. 3,
Gu, Sangdi
Olivier, Herbert
Wen, Chih-Yung
Hao, Jiaao
and
Wang, Qiu
2022.
Characterization of reflected shock tunnel air conditions using a simple method.
Physics of Fluids,
Vol. 34,
Issue. 5,
Wang, Ge
Zhou, Bocheng
Guan, Ben
and
Yang, Haiwei
2023.
Numerical investigation on expansion–deflection nozzle flow during an ascending–descending trajectory.
Physics of Fluids,
Vol. 35,
Issue. 8,
2023.
Numerical investigation on thrust characteristics of an annular expansion–deflection nozzle.
Physics of Fluids,
Vol. 35,
Issue. 5,
Redding, Jeremy
Gamertsfelder, Jacob
Bravo, Luis
and
Khare, Prashant
2023.
Thermochemical non-equilibrium hypersonic flow over a rectangular cavity embedded on a compression ramp.
Physics of Fluids,
Vol. 35,
Issue. 12,
Gu, Sangdi
Wen, Chih-Yung
Hao, Jiaao
Wang, Wentao
and
Wang, Qiu
2024.
The influence of hypersonic free-stream conicity on the flow over a sphere.
Journal of Fluid Mechanics,
Vol. 989,
Issue. ,
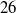 and
and 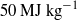 , are considered. The Mach number and unit Reynolds number per metre were 7.6, 11.0 and
, are considered. The Mach number and unit Reynolds number per metre were 7.6, 11.0 and 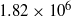 ,
, 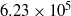 respectively. The Reynolds number based on the step height was correspondingly
respectively. The Reynolds number based on the step height was correspondingly 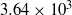 and
and 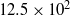 . The computations were carried out assuming the flow to be laminar throughout and the real gas effects such as thermal and chemical non-equilibrium are studied using Park’s two-temperature model with finite-rate chemistry and Gupta’s finite-rate chemistry models. In the close vicinity of the step, detailed quantification of flow features is emphasised. In particular, the presence of the Goldstein singularity at the lip and separation on the face of the step have been elucidated. Within the separated region and downstream of reattachment, the influence of real gas effects has been identified and shown to be negligible. The numerical results are compared with the available experimental data of surface heat flux downstream of the step and reasonable agreement is shown up to 30 step heights downstream.
. The computations were carried out assuming the flow to be laminar throughout and the real gas effects such as thermal and chemical non-equilibrium are studied using Park’s two-temperature model with finite-rate chemistry and Gupta’s finite-rate chemistry models. In the close vicinity of the step, detailed quantification of flow features is emphasised. In particular, the presence of the Goldstein singularity at the lip and separation on the face of the step have been elucidated. Within the separated region and downstream of reattachment, the influence of real gas effects has been identified and shown to be negligible. The numerical results are compared with the available experimental data of surface heat flux downstream of the step and reasonable agreement is shown up to 30 step heights downstream.

