Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T08:59:55.989Z Has data issue: false hasContentIssue false
  • English
  • Français

High frequency oscillatory flows in a slightly rarefied gas according to the Boltzmann–BGK equation

Published online by Cambridge University Press:  19 July 2013

Jason Nassios  and
John E. Sader
Jason Nassios
Affiliation:
Department of Mathematics and Statistics, The University of Melbourne, Victoria 3010, Australia
John E. Sader*
Affiliation:
Department of Mathematics and Statistics, The University of Melbourne, Victoria 3010, Australia Kavli Nanoscience Institute and Department of Physics, California Institute of Technology, Pasadena, CA 91125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Boltzmann equation provides a rigorous theoretical framework to study dilute gas flows at arbitrary degrees of rarefaction. Asymptotic methods have been applied to steady flows, enabling the development of analytical formulae. For unsteady (oscillatory) flows, two important limits have been studied: (i) at low oscillation frequency and small mean free path, slip models have been derived; and (ii) at high oscillation frequency and large mean free path, the leading-order dynamics are free-molecular. In this article, the complementary case of small mean free path and high oscillation frequency is examined in detail. All walls are solid and of arbitrary smooth shape. We perform a matched asymptotic expansion of the unsteady linearized Boltzmann–BGK equation in the small parameter 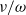$\nu / \omega $, where $\nu $ is the collision frequency of gas particles and 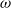$\omega $ is the characteristic oscillation frequency of the flow. Critically, an algebraic expression is derived for the perturbed mass distribution function throughout the bulk of the gas away from any walls, at all orders in the frequency ratio 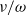$\nu / \omega $. This is supplemented by a boundary layer correction defined by a set of first-order differential equations. This system is solved explicitly and in complete generality. We thus provide analytical expressions up to first order in the frequency ratio, for the density, temperature, mean velocity and stress tensor of the gas, in terms of the temperature and mean velocity of the wall, and the applied body force. In stark contrast to other asymptotic regimes, these explicit formulae eliminate the need to solve a differential equation for a body of arbitrary geometry. To illustrate the utility of these results, we study the oscillatory thermal creep problem for which we find a tangential boundary layer flow arises at first order in the frequency ratio.

JFM classification

Rarefied Gas Flow: Kinetic theory Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Rarefied Gas Flow: Rarefied Gas Flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 729 , 25 August 2013 , pp. 1 - 46
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions. Dover.Google Scholar
Agarwal, R. K., Yun, K. Y. & Balakrishnan, R. 2001 Beyond Navier–Stokes: Burnett equations for flows in the continuum–transition regime. Phys. Fluids 13 (10), 3061.Google Scholar
Baker, L. L. & Hadjiconstantinou, N. G. 2005 Variance reduction for Monte Carlo solutions of the Boltzmann equation. Phys. Fluids 17 (5), 051703.Google Scholar
Bargatin, I., Kozinsky, I. & Roukes, M. L. 2007 Efficient electrothermal actuation of multiple modes of high-frequency nanoelectromechanical resonators. Appl. Phys. Lett. 90 (9), 093116.Google Scholar
Bhatnagar, P. L., Gross, E. P. & Krook, M. 1954 A model for collision processes in gases. Part 1. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94 (3), 511.CrossRefGoogle Scholar
Bird, G. A. 1963 Approach to translational equilibrium in a rigid sphere gas. Phys. Fluids 6, 1518–1519.Google Scholar
Bird, G. A. 1998 Recent advances and current challenges for DSMC. Comput. Maths Applics. 35 (1–2), 1–14.Google Scholar
Bittencourt, J. A. 2004 Fundamentals of Plasma Physics. Springer.Google Scholar
Bouchut, F. & Perthame, B. 1993 A BGK model for small Prandtl number in the Navier–Stokes approximation. J. Stat. Phys. 71 (1–2), 191–207.CrossRefGoogle Scholar
Brull, S. & Schneider, J. 2008 A new approach for the ellipsoidal statistical model. Contin. Mech. Thermodyn. 20 (2), 63–74.Google Scholar
Camenzind, M. 2007 Compact Objects in Astrophysics: White Dwarfs, Neutron Stars, and Black Holes. Springer.Google Scholar
Cartan, H. 1977 Course de Calcul Différentiel. Hermann.Google Scholar
Cercignani, C. 1962 Elementary solutions of the linearized gas-dynamics Boltzmann equation and their application to the slip-flow problem. Ann. Phys. 20 (2), 219–233.Google Scholar
Cercignani, C. 1964 Higher order slip according to the linearized Boltzmann equation. Tech. Rep., California University Berkeley Institute of Engineering Research.Google Scholar
Cercignani, C. 1988 The Boltzmann Equation and its Applications. Springer.CrossRefGoogle Scholar
Cercignani, C. 2000 Rarefied Gas Dynamics: From Basic Concepts to Actual Calculations. Cambridge University Press.Google Scholar
Chapman, S. 1916 On the law of distribution of molecular velocities, and on the theory of viscosity and thermal conduction, in a non-uniform simple monatomic gas. Phil. Trans. R. Soc. Lond. A 216, 279–348.Google Scholar
Chen, H., Kandasamy, S., Orszag, S., Shock, R., Succi, S. & Yakhot, V. 2003 Extended Boltzmann kinetic equation for turbulent flows. Science 301 (5633), 633–636.Google Scholar
Chun, J. & Koch, D. L. 2005 A direct simulation Monte Carlo method for rarefied gas flows in the limit of small Mach number. Phys. Fluids 17 (10), 107107.Google Scholar
Clausing, P. 1971 The flow of highly rarefied gases through tubes of arbitrary length. J. Vac. Sci. Technol. 8 (5), 636–646.Google Scholar
Dodelson, S. 2003 Modern Cosmology. Academic.Google Scholar
Dubois, J.-M., Ouanounou, G. & Rouzaire-Dubois, B. 2009 The Boltzmann equation in molecular biology. Prog. Biophys. Molecular Biol. 99 (2–3), 87–93.Google Scholar
Enskog, D. 1917 Kinetische Theorie der Vorgänge in mässig verdünnten Gasen. PhD thesis, Uppsala.Google Scholar
Gallis, M. a. & Torczynski, J. R. 2011 Investigation of the ellipsoidal–statistical Bhatnagar–Gross–Krook kinetic model applied to gas-phase transport of heat and tangential momentum between parallel walls. Phys. Fluids 23 (3), 030601.Google Scholar
Grad, H. 1958 Principles of the Kinetic Theory of Gases. Springer.Google Scholar
Hadjiconstantinou, N. G. 2005a Oscillatory shear-driven gas flows in the transition and free-molecular-flow regimes. Phys. Fluids 17 (10), 100611.CrossRefGoogle Scholar
Hadjiconstantinou, N. G. 2005b Validation of a second-order slip model for dilute gas flows. Microscale Therm. Engng 9 (2), 137–153.Google Scholar
Hadjiconstantinou, N. G., Garcia, A. L., Bazant, M. Z. & He, G. 2003 Statistical error in particle simulations of hydrodynamic phenomena. J. Comput. Phys. 187 (1), 274–297.Google Scholar
Hadjiconstantinou, N. G., Radtke, G. a. & Baker, L. L. 2010 On variance-reduced simulations of the Boltzmann transport equation for small-scale heat transfer applications. J. Heat Transfer 132 (11), 112401.Google Scholar
Hilbert, D. 1900 Mathematische Probleme. In Vortrag, Gehalten auf dem Internationalen Mathematiker, pp. 253–297. Vadenhöck and Ruprecht.Google Scholar
Hilbert, D. 1912 Grundzüge einer Allgemeinen Theorie der Linearen Integralgleichungen. Teubner.Google Scholar
Holway, L. H. 1963 Approximation procedures for kinetic theory. PhD, Harvard.Google Scholar
Holway, L. H. 1966 New statistical models for kinetic theory: methods of construction. Phys. Fluids 9 (9), 1658.Google Scholar
Homolle, T. M. M. & Hadjiconstantinou, N. G. 2007 A low-variance deviational simulation Monte Carlo for the Boltzmann equation. J. Comput. Phys. 226 (2), 2341–2358.Google Scholar
Juvé, V., Crut, A., Maioli, P., Pellarin, M., Broyer, M., Del Fatti, N. & Vallée, F. 2010 Probing elasticity at the nanoscale: terahertz acoustic vibration of small metal nanoparticles. Nano Lett. 0–5.Google Scholar
von Kármán, T. 1963 From Low-speed Aerodynamics to Astronautics. Pergamon.Google Scholar
Knudsen, M. 1909a Die Gesetze der molekular Strömung und der inneren Reibungströmung der Gase durch Röhren. Ann. Phys. 28, 75–130.Google Scholar
Knudsen, M. 1909b Eine Revision der Gleichgewichtsbedingung der Gase: Thermische Molekularströmung. Ann. Phys. 336 (1), 205–229.Google Scholar
Knudsen, M. 1910 Thermischer Molekulardruck der Gase in Röhren und porösen Körpern. Ann. Phys. 336 (3), 633–640.Google Scholar
Lagubeau, G., Le Merrer, M., Clanet, C. & Quéré, D. 2011 Leidenfrost on a ratchet. Nat. Phys. 7 (5), 395–398.Google Scholar
Lebowitz, J. L., Frisch, H. L. & Helfand, E. 1960 Nonequilibrium distribution functions in a fluid. Phys. Fluids 3, 325–338.CrossRefGoogle Scholar
Loyalka, S. K. 1971 Kinetic theory of thermal transpiration and mechanocaloric effect. Part 1. J. Chem. Phys. 55 (9), 4497.Google Scholar
Loyalka, S. K., Petrellis, N. & Storvick, T. S. 1979 Some exact numerical results for the BGK model: Couette, Poiseuille and thermal creep flow between parallel plates. Z. Angew. Math. Phys. 30 (3), 514–521.Google Scholar
Loyalka, S. K. & Tompson, R. V. 2009 The velocity slip problem: accurate solutions of the BGK model integral equation. Eur. J. Mech. B 28 (2), 211–213.Google Scholar
Manela, A. & Hadjiconstantinou, N. G. 2007 On the motion induced in a gas confined in a small-scale gap due to instantaneous boundary heating. J. Fluid Mech. 593, 453–462.Google Scholar
Maxwell, J. C. 1879 On stresses in rarified gases arising from inequalities of temperature. Phil. Trans. R. Soc. Lond. 170, 231–256.Google Scholar
Nassios, J. & Sader, J. E. 2012 Asymptotic analysis of the Boltzmann–BGK equation for oscillatory flows. J. Fluid Mech. 708 (1960), 197–249.Google Scholar
Ohwada, T. & Sone, Y. 1992 Analysis of thermal stress slip flow and negative thermophoresis using the Boltzmann equation for hard-sphere molecules. Eur. J. Mech. B 11 (4), 389–414.Google Scholar
Ohwada, T., Sone, Y. & Aoki, K. 1989 Numerical analysis of the shear and thermal creep flows of a rarefied gas over a plane wall on the basis of the linearized Boltzmann equation for hard-sphere molecules. Phys. Fluids A 1, 1588.CrossRefGoogle Scholar
Park, J. H., Bahukudumbi, P. & Beskok, A. 2004 Rarefaction effects on shear driven oscillatory gas flows: a direct simulation Monte Carlo study in the entire Knudsen regime. Phys. Fluids 16 (2), 317.CrossRefGoogle Scholar
Pelton, M., Sader, J. E., Burgin, J., Liu, M., Guyot-Sionnest, P. & Gosztola, D. 2009 Damping of acoustic vibrations in gold nanoparticles. Nat. Nanotechnology 4 (8), 492–495.Google Scholar
Preziosi, L. 1992 Thermal creep problems by the discrete Boltzmann equation. Transp. Theory Stat. Phys. 21 (3), 183–209.Google Scholar
Radtke, G. a., Hadjiconstantinou, N. G. & Wagner, W. 2011 Low-noise Monte Carlo simulation of the variable hard sphere gas. Phys. Fluids 23 (3), 030606.Google Scholar
Ramanathan, S. & Koch, D. L. 2009 An efficient direct simulation Monte Carlo method for low Mach number noncontinuum gas flows based on the Bhatnagar–Gross–Krook model. Phys. Fluids 21 (3), 033103.Google Scholar
Sharipov, F. & Kalempa, D. 2007 Gas flow near a plate oscillating longitudinally with an arbitrary frequency. Phys. Fluids 19 (1), 017110.Google Scholar
Sharipov, F. & Kalempa, D. 2008 Oscillatory Couette flow at arbitrary oscillation frequency over the whole range of the Knudsen number. Microfluid Nanofluid 4 (5), 363–374.Google Scholar
Shi, Y. & Sader, J. E. 2010 Lattice Boltzmann method for oscillatory Stokes flow with applications to micro- and nanodevices. Phys. Rev. E 81 (3), 1–14.Google Scholar
Sone, Y. 1966 Thermal creep in rarefied gas. J. Phys. Soc. Japan 21, 1836–1837.Google Scholar
Sone, Y. 1969 Asymptotic theory of flow of rarefied gas over a smooth boundary I. In Rarefied Gas Dynamics (ed. Trilling, L. & Wachman, H. Y.), p. 243. Academic.Google Scholar
Sone, Y. 1972 A flow induced by thermal stress in rarefied gas. J. Phys. Soc. Japan 33, 232–236.Google Scholar
Sone, Y. 1974 Asymptotic theory of flow of rarefied gas over a smooth boundary. Part 2. Trans. Japan. Soc. Aeronaut. Space Sci. 17, 113–122.Google Scholar
Sone, Y. 1984 Highly rarefied gas around a group of bodies with various temperature distributions. Part 1. Small temperature variation. J. Méc. Théor. Appl. 3 (2), 315–328.Google Scholar
Sone, Y. 1985 Boundary temperature effect in a highly rarefied gas. Phys. Fluids 28 (1), 419.Google Scholar
Sone, Y. 2000 Kinetic Theory and Fluid Dynamics. Birkhäuser.Google Scholar
Sone, Y. 2007 Molecular Gas Dynamics: Theory, Techniques, and Applications. Springer.CrossRefGoogle Scholar
Sone, Y., Ohwada, T. & Aoki, K. 1989 Temperature jump and Knudsen layer in a rarefied gas over a plane wall: numerical analysis of the linearized Boltzmann equation for hard-sphere molecules. Phys. Fluids A 1 (2), 363–370.Google Scholar
Struchtrup, H. 1997 The BGK-model with velocity-dependent collision frequency. Contin. Mech. Thermodyn. 9 (1), 23–31.Google Scholar
Struchtrup, H. & Torrilhon, M. 2003 Regularization of Grad’s 13 moment equations: derivation and linear analysis. Phys. Fluids 15 (9), 2668.Google Scholar
Taheri, P., Rana, A. S., Torrilhon, M. & Struchtrup, H. 2009 Macroscopic description of steady and unsteady rarefaction effects in boundary value problems of gas dynamics. Contin. Mech. Thermodyn. 21 (6), 423–443.Google Scholar
Takata, S. & Hattori, M. 2012 Asymptotic theory for the time-dependent behavior of a slightly rarefied gas over a smooth solid boundary. J. Stat. Phys. 147 (6), 1182–1215.Google Scholar
Tamada, K. & Sone, Y. 1966 Some studies on rarefied gas flows. J. Phys. Soc. Japan 21 (7), 1439–1445.Google Scholar
Tang, G., Gu, X.-J., Barber, R., Emerson, D. R. & Zhang, Y. 2008 Lattice Boltzmann simulation of nonequilibrium effects in oscillatory gas flow. Phys. Rev. E 78 (2), 1–8.Google Scholar
Torrilhon, M. & Struchtrup, H. 2008 Boundary conditions for regularized 13-moment-equations for micro-channel-flows. J. Comput. Phys. 227 (3), 1982–2011.Google Scholar
Toscani, G. 2009 Wealth redistribution in conservative linear kinetic models. Europhys. Lett. 88 (1), 10007.Google Scholar
Vargo, S. E., Muntz, E. P., Shiflett, G. R. & Tang, W. C. 1999 Knudsen compressor as a micro- and macroscale vacuum pump without moving parts or fluids. J. Vac. Sci. Technol. A 17 (4), 2308.Google Scholar
Vincenti, W. G. & Kruger, C. H. Jr 1965 Introduction to Physical Gas Dynamics, 8th edn. Krieger.Google Scholar
Wagner, W. 2008 Deviational particle Monte Carlo for the Boltzmann equation. Monte Carlo Meth. Applic. 14 (3), 191–268.Google Scholar
Welander, P. 1954 On the temperature jump in a rarefied gas. Ark. Fys. 7, 507–553.Google Scholar
Würger, A. 2011 Leidenfrost gas ratchets driven by thermal creep. Phys. Rev. Lett. 107 (16), 1–4.Google Scholar
Yap, Y. W. & Sader, J. E. 2012 High accuracy numerical solutions of the Boltzmann Bhatnagar–Gross–Krook equation for steady and oscillatory Couette flows. Phys. Fluids 24 (3), 032004.Google Scholar
Yu, H., Girimaji, S. & Luo, L.-S. 2005 Lattice Boltzmann simulations of decaying homogeneous isotropic turbulence. Phys. Rev. E 71 (1), 1–5.CrossRefGoogle ScholarPubMed
Supplementary material: File

Nassios et al. supplementary material

Unknown data file types

Download Nassios et al. supplementary material(File)
File 1.7 MB