Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T10:26:25.394Z Has data issue: false hasContentIssue false
  • English
  • Français

A hierarchical random additive model for passive scalars in wall-bounded flows at high Reynolds numbers

Published online by Cambridge University Press:  09 March 2018

Xiang I. A. Yang Open the ORCID record for Xiang I. A. Yang [Opens in a new window]  and
Mahdi Abkar Open the ORCID record for Mahdi Abkar [Opens in a new window]
Xiang I. A. Yang
Affiliation:
Center for Turbulence Research, Stanford University, Stanford, CA 94305, USA Mechanical and Nuclear Engineering, Penn State University, State College, PA 16801, USA
Mahdi Abkar*
Affiliation:
Center for Turbulence Research, Stanford University, Stanford, CA 94305, USA Department of Engineering, Aarhus University, 8000 Aarhus C, Denmark
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The kinematics of a fully developed passive scalar is modelled using the hierarchical random additive process (HRAP) formalism. Here, ‘a fully developed passive scalar’ refers to a scalar field whose instantaneous fluctuations are statistically stationary, and the ‘HRAP formalism’ is a recently proposed interpretation of the Townsend attached eddy hypothesis. The HRAP model was previously used to model the kinematics of velocity fluctuations in wall turbulence: 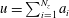$u=\sum _{i=1}^{N_{z}}a_{i}$, where the instantaneous streamwise velocity fluctuation at a generic wall-normal location $z$ is modelled as a sum of additive contributions from wall-attached eddies (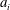$a_{i}$) and the number of addends is 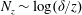$N_{z}\sim \log (\unicode[STIX]{x1D6FF}/z)$. The HRAP model admits generalized logarithmic scalings including 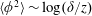$\langle \unicode[STIX]{x1D719}^{2}\rangle \sim \log (\unicode[STIX]{x1D6FF}/z)$, 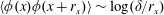$\langle \unicode[STIX]{x1D719}(x)\unicode[STIX]{x1D719}(x+r_{x})\rangle \sim \log (\unicode[STIX]{x1D6FF}/r_{x})$, 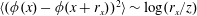$\langle (\unicode[STIX]{x1D719}(x)-\unicode[STIX]{x1D719}(x+r_{x}))^{2}\rangle \sim \log (r_{x}/z)$, where 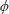$\unicode[STIX]{x1D719}$ is the streamwise velocity fluctuation, 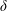$\unicode[STIX]{x1D6FF}$ is an outer length scale, 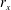$r_{x}$ is the two-point displacement in the streamwise direction and 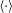$\langle \cdot \rangle$ denotes ensemble averaging. If the statistical behaviours of the streamwise velocity fluctuation and the fluctuation of a passive scalar are similar, we can expect first that the above mentioned scalings also exist for passive scalars (i.e. for 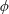$\unicode[STIX]{x1D719}$ being fluctuations of scalar concentration) and second that the instantaneous fluctuations of a passive scalar can be modelled using the HRAP model as well. Such expectations are confirmed using large-eddy simulations. Hence the work here presents a framework for modelling scalar turbulence in high Reynolds number wall-bounded flows.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 354 - 380
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Antonia, R. A. & Kawamura, H. 2009 Correlation between small-scale velocity and scalar fluctuations in a turbulent channel flow. J. Fluid Mech. 627, 1–32.CrossRefGoogle Scholar
Abkar, M., Bae, H. J. & Moin, P. 2016 Minimum-dissipation scalar transport model for large-eddy simulation of turbulent flows. Phys. Rev. Fluids 1 (4), 041701.CrossRefGoogle Scholar
Abkar, M. & Moin, P. 2017 Large-eddy simulation of thermally stratified atmospheric boundary-layer flow using a minimum dissipation model. Boundary-Layer Meteorol. 165 (3), 405–419.CrossRefGoogle ScholarPubMed
Abkar, M. & Porté-Agel, F. 2012 A new boundary condition for large-eddy simulation of boundary-layer flow over surface roughness transitions. J. Turbul. 13, 1–18.Google Scholar
Abkar, M. & Porté-Agel, F. 2014 Mean and turbulent kinetic energy budgets inside and above very large wind farms under conventionally neutral condition. Renew. Energy 70, 142–152.CrossRefGoogle Scholar
Abkar, M. & Porté-Agel, F. 2015 Influence of atmospheric stability on wind turbine wakes: a large-eddy simulation study. Phys. Fluids 27 (3), 035104.CrossRefGoogle Scholar
Abkar, M. & Porté-Agel, F. 2016 Influence of the Coriolis force on the structure and evolution of wind turbine wakes. Phys. Rev. Fluids 1, 063701.CrossRefGoogle Scholar
Albertson, J. D. & Parlange, M. B. 1999 Surface length-scales and shear stress: implications for land–atmosphere interaction over complex terrain. Water Resour. Res. 35 (7), 2121–2132.CrossRefGoogle Scholar
Andren, A., Brown, A. R., Mason, P. J., Graf, J., Schumann, U., Moeng, C.-H. & Nieuwstadt, F. T. 1994 Large-eddy simulation of a neutrally stratified boundary layer: a comparison of four computer codes. Q. J. R. Meteorol. Soc. 120 (520), 1457–1484.Google Scholar
Antonia, R. A., Abe, H. & Kawamura, H. 2009 Analogy between velocity and scalar fields in a turbulent channel flow. J. Fluid Mech. 628, 241–268.CrossRefGoogle Scholar
Antonia, R. A. & Chambers, A. J. 1980 On the correlation between turbulent velocity and temperature derivatives in the atmospheric surface layer. Boundary-Layer Meteorol. 18 (4), 399–410.CrossRefGoogle Scholar
Antonia, R. A. & Van Atta, C. W. 1975 On the correlation between temperature and velocity dissipation fields in a heated turbulent jet. J. Fluid Mech. 67 (02), 273–288.CrossRefGoogle Scholar
Antonia, R. A., Zhu, Y., Anselmet, F. & Ould-Rouis, M. 1996 Comparison between the sum of second-order velocity structure functions and the second-order temperature structure function. Phys. Fluids 8 (11), 3105–3111.CrossRefGoogle Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017 Reynolds number trend of hierarchies and scale interactions in turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 375 (2089), 20160077.Google ScholarPubMed
Baars, W. J., Talluru, K. M., Hutchins, N. & Marusic, I. 2015 Wavelet analysis of wall turbulence to study large-scale modulation of small scales. Exp. Fluid 56 (10), 188.CrossRefGoogle Scholar
Bose, S. T. & Moin, P. 2014 A dynamic slip boundary condition for wall-modeled large-eddy simulation. Phys. Fluids 26 (1), 015104.CrossRefGoogle Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. 2005 A scale-dependent lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17 (2), 025105.CrossRefGoogle Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. B. 2004 Large-eddy simulation of neutral atmospheric boundary layer flow over heterogeneous surfaces: blending height and effective surface roughness. Water Resour. Res. 40 (2), W02505.CrossRefGoogle Scholar
Choi, H. & Moin, P. 2012 Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 24 (1), 011702.CrossRefGoogle Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22 (4), 469–473.CrossRefGoogle Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.CrossRefGoogle Scholar
Fulachier, L. & Antonia, R. A. 1984 Spectral analogy between temperature and velocity fluctuations in several turbulent flows. Intl J. Heat Mass Transfer 27 (7), 987–997.CrossRefGoogle Scholar
Fulachier, L. & Dumas, R. 1976 Spectral analogy between temperature and velocity fluctuations in a turbulent boundary layer. J. Fluid Mech. 77 (02), 257–277.CrossRefGoogle Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.CrossRefGoogle Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 3, 1760–1765.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 094501.CrossRefGoogle ScholarPubMed
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. 365 (1852), 647–664.Google ScholarPubMed
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
Kader, B. A. 1981 Temperature and concentration profiles in fully turbulent boundary layers. Intl J. Heat Mass Tranfer 24 (9), 1541–1544.CrossRefGoogle Scholar
Kasagi, N. & Ohtsubo, Y. 1993 Direct numerical simulation of low Prandtl number thermal field in a turbulent channel flow. In Turbulent Shear Flows 8, pp. 97–119. Springer.CrossRefGoogle Scholar
Kasagi, N., Tomita, Y. & Kuroda, A. 1992 Direct numerical simulation of passive scalar field in a turbulent channel flow. J. Heat Transfer 114 (3), 598–606.CrossRefGoogle Scholar
Kawai, S. & Larsson, J. 2012 Wall-modeling in large eddy simulation: length scales, grid resolution, and accuracy. Phys. Fluids 24 (1), 015105.CrossRefGoogle Scholar
Kawamura, H., Abe, H. & Shingai, K. 2000 DNS of turbulence and heat transport in a channel flow with different Reynolds and Prandtl numbers and boundary conditions. In Proceedings of the 3rd International Symposium on Turbulence, Heat and Mass Transfer, Aichi Shuppan, Japan, pp. 15–32.Google Scholar
Kim, J. & Moin, P. 1989 Transport of passive scalars in a turbulent channel flow. In Turbulent Shear Flows 6, pp. 85–96. Springer.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. In Dokl. Akad. Nauk SSSR, vol. 30, pp. 301–305. JSTOR.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13 (01), 82–85.CrossRefGoogle Scholar
Kong, H., Choi, H. & Lee, J. S. 2000 Direct numerical simulation of turbulent thermal boundary layers. Phys. Fluids 12 (10), 2555–2568.CrossRefGoogle Scholar
Lavertu, R. A. & Mydlarski, L. 2005 Scalar mixing from a concentrated source in turbulent channel flow. J. Fluid Mech. 528, 135–172.CrossRefGoogle Scholar
Lu, H. & Porté-Agel, F. 2013 A modulated gradient model for scalar transport in large-eddy simulation of the atmospheric boundary layer. Phys. Fluids 25 (1), 015110.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Marušic, I. & Perry, A. E. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.CrossRefGoogle Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32 (1), 1–32.CrossRefGoogle Scholar
Meneveau, C. & Marusic, I. 2013 Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech. 719, R1.CrossRefGoogle Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4 (5), 101–104.CrossRefGoogle Scholar
Moin, P., Squires, K. D. & Lee, S. 1991 A dynamic subgrid-scale model for compressible turbulence and scalar transport. Phys. Fluids 3, 2746.CrossRefGoogle Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 2. MIT Press.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.CrossRefGoogle Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k -1 law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95 (7), 074501.CrossRefGoogle Scholar
Obukhov, A. M. 1949 The local structure of atmospheric turbulence. Dokl. Akad. Nauk. SSSR 67, 643–646.Google Scholar
Park, G. I. & Moin, P. 2014 An improved dynamic non-equilibrium wall-model for large eddy simulation. Phys. Fluids 26 (1), 37–48.CrossRefGoogle Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A. E. & Marušic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34 (1), 349–374.CrossRefGoogle Scholar
Porté-Agel, F. 2004 A scale-dependent dynamic model for scalar transport in large-eddy simulations of the atmospheric boundary layer. Boundary-Layer Meteorol 112 (1), 81–105.CrossRefGoogle Scholar
Porté-Agel, F., Meneveau, C. & Parlange, M. B. 2000 A scale-dependent dynamic model for large-eddy simulation: application to a neutral atmospheric boundary layer. J. Fluid Mech. 415, 261–284.CrossRefGoogle Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13 (2), 297–319.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 1999 Boundary-layer Theory. Springer.Google Scholar
Shraiman, B. I. & Siggia, E. D. 2000 Scalar turbulence. Nature 405 (6787), 639–646.CrossRefGoogle ScholarPubMed
de Silva, C., Marusic, I., Woodcock, J. D. & Meneveau, C. 2015 Scaling of second-and higher-order structure functions in turbulent boundary layers. J. Fluid Mech. 769, 654–686.CrossRefGoogle Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. Mon. Weath. Rev. 91 (3), 99–164.2.3.CO;2>CrossRefGoogle Scholar
Sreenivasan, K. R. 1991 On local isotropy of passive scalars in turbulent shear flows. Proc. R. Soc. Lond. A 434 (1890), 165–182.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.CrossRefGoogle Scholar
Stevens, R. J., Wilczek, M. & Meneveau, C. 2014 Large-eddy simulation study of the logarithmic law for second-and higher-order moments in turbulent wall-bounded flow. J. Fluid Mech. 757, 888–907.CrossRefGoogle Scholar
Stoll, R. & Porté-Agel, F. 2006 Dynamic subgrid scale models for momentum and scalar fluxes in large eddy simulations of neutrally stratified atmospheric boundary layers over heterogeneous terrain. Water Resour. Res. 42 (1), W01409.CrossRefGoogle Scholar
Stoll, R. & Porté-Agel, F. 2009 Surface heterogeneity effects on regional-scale fluxes in stable boundary layers: surface temperature transitions. J. Atmos. Sci. 66 (2), 412–431.CrossRefGoogle Scholar
Strutt, J. W. & Rayleigh, L. 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14 (1), 8.Google Scholar
Stull, R. 1988 An Introduction to Boundary-layer Meteorology. Kluwer Academic Publishers.CrossRefGoogle Scholar
Subramanian, C. S. & Antonia, R. A. 1981 Effect of Reynolds number on a slightly heated turbulent boundary layer. Intl J. Heat Mass Transfer 24 (11), 1833–1846.CrossRefGoogle Scholar
Talluru, K. M., Hernandez-Silva, C., Philip, J. & Chauhan, K. A. 2017 Measurements of scalar released from point sources in a turbulent boundary layer. Meas. Sci. Technol. 28 (5), 055801.CrossRefGoogle Scholar
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. In Proceedings of the Royal Society London A Mat., vol. 201, pp. 192–196. The Royal Society.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flows. Cambridge University Press.Google Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32 (1), 203–240.CrossRefGoogle Scholar
Watanabe, T. & Gotoh, T. 2004 Statistics of a passive scalar in homogeneous turbulence. New J. Phys. 6 (1), 40.CrossRefGoogle Scholar
Yang, X. I. A. 2016 On the mean flow behaviour in the presence of regional-scale surface roughness heterogeneity. Boundary-Layer Meteorol. 161 (1), 127–143.CrossRefGoogle Scholar
Yang, X. I. A., Baidya, R., Johnson, P., Maruisc, I. & Meneveau, C. 2017a Structure function tensor scaling in the logarithmic region derived from the attached eddy model of wall-bounded turbulent flows. Phys. Rev. Fluids 2 (6), 064602.CrossRefGoogle Scholar
Yang, X. I. A., Marusic, I. & Meneveau, C. 2016a Hierarchical random additive process and logarithmic scaling of generalized high order, two-point correlations in turbulent boundary layer flow. Phys. Rev. Fluids 1 (2), 024402.CrossRefGoogle Scholar
Yang, X. I. A., Marusic, I. & Meneveau, C. 2016b Moment generating functions and scaling laws in the inertial layer of turbulent wall-bounded flows. J. Fluid Mech. 791, R2.CrossRefGoogle Scholar
Yang, X. I. A. & Meneveau, C. 2016 Recycling inflow method for simulations of spatially evolving turbulent boundary layers over rough surfaces. J. Turbul. 17 (1), 75–93.CrossRefGoogle Scholar
Yang, X. I. A., Meneveau, C., Marusic, I. & Biferale, L. 2016c Extended self-similarity in moment-generating-functions in wall-bounded turbulence at high Reynolds number. Phys. Rev. Fluids 1 (4), 044405.CrossRefGoogle Scholar
Yang, X. I. A., Park, G. & Moin, P. 2017b Log-layer mismatch and modeling of the fluctuating wall stress in wall-modeled large-eddy simulations. Phys. Rev. Fluids 2 (10), 104601.CrossRefGoogle ScholarPubMed
Yang, X. I. A., Sadique, J., Mittal, R. & Meneveau, C. 2015 Integral wall model for large eddy simulations of wall-bounded turbulent flows. Phys. Fluids 27 (2), 025112.CrossRefGoogle Scholar
Yang, X. I. A., Sadique, J., Mittal, R. & Meneveau, C. 2016d Exponential roughness layer and analytical model for turbulent boundary layer flow over rectangular-prism roughness elements. J. Fluid Mech. 789, 127–165.CrossRefGoogle Scholar