Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T12:26:47.019Z Has data issue: false hasContentIssue false
  • English
  • Français

Helical vortex filament motion under the non-local Biot–Savart model

Published online by Cambridge University Press:  03 December 2014

Robert A. Van Gorder
Robert A. Van Gorder*
Affiliation:
Department of Mathematics, University of Central Florida, Orlando, FL 32816-1364, USA
*
†Present address: Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, UK. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The thin helical vortex filament is one of the fundamental exact solutions possible under the local induction approximation (LIA). The LIA is itself an approximation to the non-local Biot–Savart dynamics governing the self-induced motion of a vortex filament, and helical filaments have also been considered for the Biot–Savart dynamics, under a variety of configurations and assumptions. We study the motion of such a helical filament in the Cartesian reference frame by determining the curve defining this filament mathematically from the Biot–Savart model. In order to do so, we consider a matched approximation to the Biot–Savart dynamics, with local effects approximated by the LIA in order to avoid the logarithmic singularity inherent in the Biot–Savart formulation. This, in turn, allows us to determine the rotational and translational velocity of the filament in terms of a local contribution (which is exactly that which is found under the LIA) and a non-local contribution, each of which depends on the wavenumber, 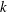$k$, and the helix diameter, 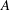$A$. Performing our calculations in such a way, we can easily compare our results to those of the LIA. For small 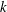$k$, the transverse velocity scales as 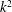$k^{2}$, while for large 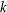$k$, the transverse velocity scales as 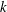$k$. On the other hand, the rotational velocity attains a maximum value at some finite 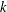$k$, which corresponds to the wavenumber giving the maximal torsion.

JFM classification

Mathematical Foundations: Computational methods Mathematical Foundations: Mathematical Foundations Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 762 , 10 January 2015 , pp. 141 - 155
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arms, R. J. & Hama, F. R. 1965 Localized-induction concept on a curved vortex and motion of an elliptic vortex ring. Phys. Fluids 8, 553.CrossRefGoogle Scholar
Bekarevich, I. L. & Khalatnikov, I. M. 1961 Phenomenological derivation of the equations of vortex motion in He II. Sov. Phys. JETP 13, 643.Google Scholar
Boersma, J. & Wood, D. H. 1999 On the self-induced motion of a helical vortex. J. Fluid Mech. 384, 263.Google Scholar
Boffetta, G., Celani, A., Dezzani, D., Laurie, J. & Nazarenko, S. 2009 Modeling Kelvin wave cascades in superfluid helium. J. Low Temp. Phys. 156, 193.CrossRefGoogle Scholar
Da Rios, L. S. 1906 Sul moto d’un liquido indefinite con un filetto vorticoso di forma qualunque. Rend. Circ. Mat. Palermo 22, 117.CrossRefGoogle Scholar
Hall, H. E. & Vinen, W. F. 1956a The rotation of liquid helium II. I. Experiments on the propagation of second sound in uniformly rotating helium II. Proc. R. Soc. Lond. A 238, 204.Google Scholar
Hall, H. E. & Vinen, W. F. 1956b The rotation of liquid helium II. II. The theory of mutual friction in uniformly rotating helium II. Proc. R. Soc. Lond. A 238, 215.Google Scholar
Kida, S. 1981 A vortex filament moving without change of form. J. Fluid Mech. 112, 397.Google Scholar
Moore, D. W. & Saffman, P. G. 1972 The motion of a vortex filament with axial flow. Phil. Trans. R. Soc. Lond. A 272, 403.Google Scholar
Ricca, R. L. 1991 Rediscovery of Da Rios equations. Nature 352, 561.Google Scholar
Ricca, R. L. 1994 The effect of torsion on the motion of a helical vortex filament. J. Fluid Mech. 273, 241.Google Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Schwarz, K. W. 1985 Three-dimensional vortex dynamics in superfluid $^{4}\text{He}$ : line–line and line–boundary interactions. Phys. Rev. B 31, 5782.Google Scholar
Sonin, E. B. 2012 Dynamics of helical vortices and helical-vortex rings. Europhys. Lett. 97, 46002.Google Scholar
Van Gorder, R. A. 2014a Quantum vortex dynamics under the tangent representation of the local induction approximation. J. Fluid Mech. 740, 5.Google Scholar
Van Gorder, R. A. 2014b Decay of helical Kelvin waves on a quantum vortex filament. Phys. Fluids 26, 075101.Google Scholar
Widnall, S. E. 1972 The stability of a helical vortex filament. J. Fluid Mech. 54, 641.CrossRefGoogle Scholar
Zhou, H. 1997 On the motion of slender vortex filaments. Phys. Fluids 9, 970.Google Scholar