Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Plumley, Meredith
and
Julien, Keith
2019.
Scaling Laws in Rayleigh‐Bénard Convection.
Earth and Space Science,
Vol. 6,
Issue. 9,
p.
1580.
Zürner, Till
Schindler, Felix
Vogt, Tobias
Eckert, Sven
and
Schumacher, Jörg
2020.
Flow regimes of Rayleigh–Bénard convection in a vertical magnetic field.
Journal of Fluid Mechanics,
Vol. 894,
Issue. ,
Akhmedagaev, R.
Zikanov, O.
Krasnov, D.
and
Schumacher, J.
2020.
Turbulent Rayleigh–Bénard convection in a strong vertical magnetic field.
Journal of Fluid Mechanics,
Vol. 895,
Issue. ,
Zürner, Till
2020.
Refined mean field model of heat and momentum transfer in magnetoconvection.
Physics of Fluids,
Vol. 32,
Issue. 10,
Maffei, S.
Krouss, M.J.
Julien, K.
and
Calkins, M.A.
2021.
On the inverse cascade and flow speed scaling behaviour in rapidly rotating Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
Yan, M.
Tobias, S.M.
and
Calkins, M.A.
2021.
Scaling behaviour of small-scale dynamos driven by Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Vogt, Tobias
Yang, Juan-Cheng
Schindler, Felix
and
Eckert, Sven
2021.
Free-fall velocities and heat transport enhancement in liquid metal magneto-convection.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Zikanov, Oleg
Belyaev, Ivan
Listratov, Yaroslav
Frick, Peter
Razuvanov, Nikita
and
Sviridov, Valentin
2021.
Mixed Convection in Pipe and Duct Flows With Strong Magnetic Fields.
Applied Mechanics Reviews,
Vol. 73,
Issue. 1,
Naskar, Souvik
and
Pal, Anikesh
2022.
Direct numerical simulations of optimal thermal convection in rotating plane layer dynamos.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Nicoski, Justin A.
Yan, Ming
and
Calkins, Michael A.
2022.
Quasistatic magnetoconvection with a tilted magnetic field.
Physical Review Fluids,
Vol. 7,
Issue. 4,
Xu, Yufan
Horn, Susanne
and
Aurnou, Jonathan M.
2022.
Thermoelectric precession in turbulent magnetoconvection.
Journal of Fluid Mechanics,
Vol. 930,
Issue. ,
Yan, Ming
and
Calkins, Michael A.
2022.
Strong large scale magnetic fields in rotating convection-driven dynamos: The important role of magnetic diffusion.
Physical Review Research,
Vol. 4,
Issue. 1,
Gürdal, Mehmet
Arslan, Kamil
Gedik, Engin
and
Minea, Alina Adriana
2022.
Effects of using nanofluid, applying a magnetic field, and placing turbulators in channels on the convective heat transfer: A comprehensive review.
Renewable and Sustainable Energy Reviews,
Vol. 162,
Issue. ,
p.
112453.
Gopinath, Venkatesh
Fournier, Alexandre
and
Gastine, Thomas
2022.
An assessment of implicit-explicit time integrators for the pseudo-spectral approximation of Boussinesq thermal convection in an annulus.
Journal of Computational Physics,
Vol. 460,
Issue. ,
p.
110965.
Aggarwal, Ashna
Aurnou, Jonathan M.
and
Horn, Susanne
2022.
Magnetic damping of jet flows in quasi-two-dimensional Rayleigh-Bénard convection.
Physical Review E,
Vol. 106,
Issue. 4,
Yan, Ming
and
Calkins, Michael A.
2022.
Asymptotic behaviour of rotating convection-driven dynamos in the plane layer geometry.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Jermyn, Adam S.
Anders, Evan H.
Lecoanet, Daniel
and
Cantiello, Matteo
2022.
An Atlas of Convection in Main-sequence Stars.
The Astrophysical Journal Supplement Series,
Vol. 262,
Issue. 1,
p.
19.
Xia, Ke-Qing
Huang, Shi-Di
Xie, Yi-Chao
and
Zhang, Lu
2023.
Tuning heat transport via coherent structure manipulation: recent advances in thermal turbulence.
National Science Review,
Vol. 10,
Issue. 6,
Cresswell, Imogen G.
Anders, Evan H.
Brown, Benjamin P.
Oishi, Jeffrey S.
and
Vasil, Geoffrey M.
2023.
Force balances in strong-field magnetoconvection simulations.
Physical Review Fluids,
Vol. 8,
Issue. 9,
Chen, Zhao-Qi
Wang, Zeng-Hui
Chen, Long
and
Ahmed, Mahmoud
2023.
Heat Transfer Enhancement of Liquid Metal Thermal Convection Affected by the Seebeck Effect and Magnetic Field.
International Journal of Energy Research,
Vol. 2023,
Issue. ,
p.
1.
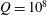 $Q=10^{8}$ over a broad range of Rayleigh numbers
$Q=10^{8}$ over a broad range of Rayleigh numbers 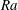 $Ra$. Three magnetoconvection regimes are identified: two of the regimes are magnetically constrained in the sense that a leading-order balance exists between the Lorentz and buoyancy forces, whereas the third regime is characterized by unbalanced dynamics that is similar to non-magnetic convection. Each regime is distinguished by flow morphology, momentum and heat equation balances, and heat transport behaviour. One of the magnetically constrained regimes appears to represent an ‘ultimate’ magnetoconvection regime in the dual limit of asymptotically large buoyancy forcing and magnetic field strength; this regime is characterized by an interconnected network of anisotropic, spatially localized fluid columns aligned with the direction of the imposed magnetic field that remain quasi-laminar despite having large flow speeds. As for non-magnetic convection, heat transport is controlled primarily by the thermal boundary layer. Empirically, the scaling of the heat transport and flow speeds with
$Ra$. Three magnetoconvection regimes are identified: two of the regimes are magnetically constrained in the sense that a leading-order balance exists between the Lorentz and buoyancy forces, whereas the third regime is characterized by unbalanced dynamics that is similar to non-magnetic convection. Each regime is distinguished by flow morphology, momentum and heat equation balances, and heat transport behaviour. One of the magnetically constrained regimes appears to represent an ‘ultimate’ magnetoconvection regime in the dual limit of asymptotically large buoyancy forcing and magnetic field strength; this regime is characterized by an interconnected network of anisotropic, spatially localized fluid columns aligned with the direction of the imposed magnetic field that remain quasi-laminar despite having large flow speeds. As for non-magnetic convection, heat transport is controlled primarily by the thermal boundary layer. Empirically, the scaling of the heat transport and flow speeds with 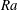 $Ra$ appear to be independent of the thermal Prandtl number within the magnetically constrained, high-
$Ra$ appear to be independent of the thermal Prandtl number within the magnetically constrained, high-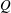 $Q$ regimes.
$Q$ regimes.