Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T05:16:08.614Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat flux enhancement by regular surface roughness in turbulent thermal convection

Published online by Cambridge University Press:  11 December 2014

Sebastian Wagner  and
Olga Shishkina
Sebastian Wagner*
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, Am Faßberg 17, 37077 Göttingen, Germany German Aerospace Center (DLR), Institute for Aerodynamics and Flow Technology, Bunsenstraße 10, 37073 Göttingen, Germany
Olga Shishkina
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, Am Faßberg 17, 37077 Göttingen, Germany German Aerospace Center (DLR), Institute for Aerodynamics and Flow Technology, Bunsenstraße 10, 37073 Göttingen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations (DNS) of turbulent thermal convection in a box-shaped domain with regular surface roughness at the heated bottom and cooled top surfaces are conducted for Prandtl number 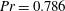$\mathit{Pr}=0.786$ and Rayleigh numbers 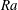$\mathit{Ra}$ between 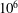$10^{6}$ and 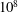$10^{8}$. The surface roughness is introduced by four parallelepiped equidistantly distributed obstacles attached to the bottom plate, and four obstacles located symmetrically at the top plate. By varying 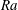$\mathit{Ra}$ and the height and width of the obstacles, we investigate the influence of the regular wall roughness on the turbulent heat transport, measured by the Nusselt number 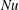$\mathit{Nu}$. For fixed 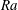$\mathit{Ra}$, the change in the value of 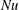$\mathit{Nu}$ is determined not only by the covering area of the surface, i.e. the obstacle height, but also by the distance between the obstacles. The heat flux enhancement is found to be largest for wide cavities between the obstacles which can be ‘washed out’ by the flow. This is also manifested in an empirical relation, which is based on the DNS data. We further discuss theoretical limiting cases for very wide and very narrow obstacles and combine them into a simple model for the heat flux enhancement due to the wall roughness, without introducing any free parameters. This model predicts well the general trends and the order of magnitude of the heat flux enhancement obtained in the DNS. In the 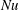$\mathit{Nu}$ versus 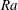$\mathit{Ra}$ scaling, the obstacles work in two ways: for smaller 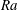$\mathit{Ra}$ an increase of the scaling exponent compared to the smooth case is found, which is connected to the heat flux entering the cavities from below. For larger 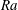$\mathit{Ra}$ the scaling exponent saturates to the one for smooth plates, which can be understood as a full washing-out of the cavities. The latter is also investigated by considering the strength of the mean secondary flow in the cavities and its relation to the wind (i.e. the large-scale circulation), that develops in the core part of the domain. Generally, an increase in the roughness height leads to stronger flows both in the cavities and in the bulk region, while an increase in the width of the obstacles strengthens only the large-scale circulation of the fluid and weakens the secondary flows. An increase of the Rayleigh number always leads to stronger flows, both in the cavities and in the bulk.

JFM classification

Convection: Convection in cavities Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 763 , 25 January 2015 , pp. 109 - 135
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.Google Scholar
Bailon-Cuba, J., Shishkina, O., Wagner, C. & Schumacher, J. 2012 Low-dimensional model of turbulent mixed convection in a complex domain. Phys. Fluids 24, 107101.CrossRefGoogle Scholar
Chandra, M. & Verma, M. K. 2013 Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett. 110, 114503.CrossRefGoogle ScholarPubMed
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.CrossRefGoogle ScholarPubMed
Ciliberto, S. & Laroche, C. 1999 Random roughness of boundary increases the turbulent scaling exponents. Phys. Rev. Lett. 82, 3998–4001.Google Scholar
Du, Y. B. & Tong, P. 1998 Enhanced heat transport in turbulent convection over a rough surface. Phys. Rev. Lett. 81, 987–990.Google Scholar
Du, Y. B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.Google Scholar
Herwig, H., Gloss, D. & Wenterodt, T. 2008 A new approach to understanding and modelling the influence of wall roughness on friction factors for pipe and channel flows. J. Fluid Mech. 613, 35–53.Google Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement induced heat-transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111, 104501.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Kaczorowski, M., Shishkina, O., Shishkin, A., Wagner, C. & Xia, K.-Q. 2011 Analysis of the large-scale circulation and the boundary layers in turbulent Rayleigh–Bénard convection. In Direct and Large-Eddy Simulation VIII (ed. Kuerten, H., Geurts, B., Armenio, V. & Fröhlich, J.), pp. 383–388. Springer.Google Scholar
Koerner, M., Shishkina, O., Wagner, C. & Thess, A. 2013 Properties of large-scale flow structures in an isothermal ventilated room. Build. Environ. 59, 563–574.CrossRefGoogle Scholar
Kraichnan, R. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5, 1374–1389.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn, Course of Theoretical Physics, vol. 6. Butterworth Heinemann.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Nikuradse, J. 1933 Strömungsgesetze in Rauhen Rohren, Forschungsheft, vol. 361. Verein Deutscher Ingenieure.Google Scholar
Pohlhausen, E. 1921 Der Wärmeaustausch zwischen festen Körpern und Flüssigkeiten mit kleiner Reibung und kleiner Wärmeleitung. Z. Angew. Math. Mech. 1, 115–121.Google Scholar
Qiu, X.-L., Xia, K.-Q. & Tong, P. 2005 Experimental study of velocity boundary layer near a rough conducting surface in turbulent natural convection. J. Turbul. 30, 1–13.Google Scholar
Roche, P.-E., Castaing, B., Chabaud, B. & Herbal, B. 2001 Observation of the 1/2 power law in Rayleigh–Bénard convection. Phys. Rev. E 63, 045303.CrossRefGoogle Scholar
Salort, J., Liot, O., Rusaouen, E., Seychelles, F., Tisserand, J.-C., Creyssels, M., Castaing, B. & Chillà, F. 2014 Thermal boundary layer near roughnesses in turbulent Rayleigh–Bénard convection: flow structure and multistability. Phys. Fluids 26, 015112.Google Scholar
Schmalzl, J., Breuer, M. & Hansen, U. 2004 On the validity of two-dimensional numerical approaches to time-dependend thermal convection. Europhys. Lett. 67, 390–396.Google Scholar
Shen, Y., Xia, K.-Q. & Tong, P. 1996 Turbulent convection over rough surfaces. Phys. Rev. Lett. 76, 908–911.CrossRefGoogle ScholarPubMed
Shishkina, O., Horn, S. & Wagner, S. 2013 Falkner–Skan boundary layer approximation in Rayleigh–Bénard convection. J. Fluid Mech. 730, 442–463.Google Scholar
Shishkina, O., Shishkin, A. & Wagner, C. 2009 Simulation of turbulent thermal convection in complicated domains. J. Comput. Appl. Maths 226, 336–344.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.Google Scholar
Shishkina, O. & Wagner, C. 2011 Modelling the influence of wall roughness on heat transfer in thermal convection. J. Fluid Mech. 686, 568–582.CrossRefGoogle Scholar
Shishkina, O. & Wagner, C. 2012 A numerical study of turbulent mixed convection in an enclosure with heated rectangular elements. J. Turbul. 13, 1–21.Google Scholar
Shishkina, O., Wagner, S. & Horn, S. 2014 Influence of the angle between the wind and the isothermal surfaces on the boundary layer structures in turbulent thermal convection. Phys. Rev. E 89, 033014.Google Scholar
Stringano, G., Pascazio, G. & Verzicco, R. 2006 Turbulent thermal convection over grooved plates. J. Fluid Mech. 557, 307–336.Google Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.Google Scholar
Tisserand, J. C., Creyssels, M., Gasteuil, Y., Pabiou, H., Gibert, M., Castaing, B. & Chillà, F. 2011 Comparison between rough and smooth plates within the same Rayleigh–Bénard cell. Phys. Fluids 23, 015105.Google Scholar
Vasil’ev, A. Y. & Frick, P. G. 2011 Reversals of large-scale circulation in turbulent convection in rectangular cavities. JETP Lett. 93, 330–344.Google Scholar
Villermaux, E. 1998 Transfer at rough sheared interfaces. Phys. Rev. Lett. 81, 4859–4862.Google Scholar
Wagner, S. & Shishkina, O. 2013 Aspect ratio dependency of Rayleigh–Bénard convection in box-shaped containers. Phys. Fluids 25, 085110.Google Scholar
Wagner, S., Shishkina, O. & Wagner, C. 2012 Boundary layers and wind in cylindrical Rayleigh–Bénard cells. J. Fluid Mech. 697, 336–366.Google Scholar
Xia, K.-Q., Sun, C. & Zhou, S. 2003 Particle image velocimetry measurement of the velocity field in turbulent thermal convection. Phys. Rev. E 68, 066303.CrossRefGoogle ScholarPubMed
Zhou, Q., Liu, B.-F., Li, C.-M. & Zhong, B.-C. 2012 Aspect ratio dependence of the heat transport by turbulent Rayleigh–Bénard convection in rectangular cells. J. Fluid Mech. 710, 260–276.CrossRefGoogle Scholar
Zhou, Q. & Xia, K.-Q. 2013 Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell. J. Fluid Mech. 721, 199–224.Google Scholar