Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-10T05:54:59.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat flux correlation for high-speed flow in the transitional regime

Published online by Cambridge University Press:  08 March 2016

Narendra Singh  and
Thomas E. Schwartzentruber
Narendra Singh*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Thomas E. Schwartzentruber
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An analytical correlation is developed for stagnation-point heat flux on spherical objects travelling at high velocity which is accurate for conditions ranging from the continuum to the free-molecular flow regime. Theoretical analysis of the Burnett and super-Burnett equations is performed using simplifications from shock-wave and boundary-layer theory to determine the relative contribution of higher-order heat flux terms compared with the Fourier heat flux (assumed in the Navier–Stokes equations). 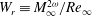A rarefaction parameter ($W_{r}\equiv M_{\infty }^{2{\it\omega}}/Re_{\infty }$), based on the free-stream Mach number (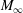$M_{\infty }$), the Reynolds number (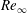$Re_{\infty }$) and the viscosity–temperature index (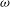${\it\omega}$), is identified as a better correlating parameter than the Knudsen number in the transition regime. By studying both the Burnett and super-Burnett equations, a general form for the entire series of higher-order heat flux contributions is obtained. The resulting heat flux expression includes terms with dependence on gas properties, stagnation to wall-temperature ratio and a main dependence on powers of the rarefaction parameter 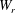$W_{r}$. The expression is applied as a correction to the Fourier heat flux and therefore can be combined with any continuum-based correlation of choice. In the free-molecular limit, a bridging function is used to ensure consistency with well-established free-molecular flow theory. The correlation is then fitted to direct simulation Monte Carlo (DSMC) solutions for stagnation-point heat flux in high-speed nitrogen flows. The correlation is shown to accurately capture the variation in heat flux predicted by the DSMC method in the transition flow regime, while limiting to both continuum and free-molecular values.

JFM classification

Aerodynamics: Aerodynamics Compressible Flows: Compressible Flows Rarefied Gas Flow: Rarefied Gas Flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 792 , 10 April 2016 , pp. 981 - 996
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agrawal, A. & Dongari, N. 2011 Application of Navier–Stokes equations to high Knudsen number flow in a fine capillary. Intl J. Microscale Nanoscale Therm. Fluid Transport Phenomena 3, 125–130.Google Scholar
Agarwal, R. K., Yun, K. Y. & Balakrishnan, R. 2001 Beyond Navier–Stokes Burnett equations for flows in the continuum transition regime. Phys. Fluids 13, 3061–3085.Google Scholar
Akintunde, A. & Petculescu, A. 2014 Infrasonic attenuation in the upper mesosphere–lower thermosphere: a comparison between Navier–Stokes and Burnett predictions. J. Acoust. Soc. Am. 136 (4), 1483–1486.Google Scholar
Anderson, J. D. 1989 Hypersonic and High Temperature Gas Dynamics. McGraw-Hill.Google Scholar
Balakrishnan, R.1999 Entropy consistent formulation and numerical simulation of the BGK–Burnett equations for hypersonic flows in the continuum-transition regime. PhD thesis, Wichita State University.Google Scholar
Bird, G. A. 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Clarendon.Google Scholar
Bobylev, A. V. 1982 The Chapman–Enskog and Grad methods for solving the Boltzmann equation. Sov. Phys. Dokl. 27, 29.Google Scholar
Brandis, A. M. & Johnston, C. O.2014 Characterization of Stagnation-Point Heat Flux for Earth Entry. AIAA 2014-2374. 20 p.Google Scholar
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases. Cambridge University Press.Google Scholar
Chen, X.-X., Wang, Z.-H. & Yu, Y.-L. 2014 Nonlinear shear and heat transfer in hypersonic rarefied flows past flat plates. AIAA J. 53 (2), 413–419.Google Scholar
Cheng, H. K. 1961 Hypersonic shock-layer theory of the stagnation region at low Reynolds number. In Proceedings of the 1961 Heat Transfer and Fluid Mechanics Institute, Palo Alto, pp. 161–175. Stanford University Press.Google Scholar
Fay, J. A. & Riddell, F. R. 1958 Theory of stagnation point in dissociated air. J. Aeronaut. Sci. 25, 73–85.Google Scholar
García-Colín, L. S., Velasco, R. M. & Uribe, F. J. 2008 Beyond the Navier–Stokes equations: Burnett hydrodynamics. Phys. Rep. 465 (4), 149–189.Google Scholar
Glass, C. E. & Moss, J. N. 2001 Aerothermodynamic characteristics in the hypersonic continuum–rarefied transitional regime. In 35th AIAA Thermophysics Conference, p. 2962. AIAA.Google Scholar
Gu, X.-J. & Emerson, D. R. 2009 A high-order moment approach for capturing non-equilibrium phenomena in the transition regime. J. Fluid Mech. 636, 177–216.Google Scholar
Gu, X.-J., Emerson, D. R. & Tang, G.-H. 2009 Kramers’ problem and the Knudsen minimum: a theoretical analysis using a linearized 26-moment approach. Contin. Mech. Thermodyn. 21 (5), 345–360.Google Scholar
He, Y., Tang, X. & Pu, Y. 2008 Modeling shock waves in an ideal gas: combining the Burnett approximation and Holian’s conjecture. Phys. Rev. E 78 (1), 017301.CrossRefGoogle Scholar
Holman, T. D. & Boyd, I. D. 2009 Effects of continuum breakdown on the surface properties of a hypersonic sphere. J. Thermophys. Heat Transfer 23 (4), 660–673.Google Scholar
Holman, T. D. & Boyd, I. D. 2011 Effects of continuum breakdown on hypersonic aerothermodynamics for reacting flow. Phys. Fluids 23 (2), 027101.Google Scholar
Khalil, N., Garzó, V. & Santos, A. 2014 Hydrodynamic Burnett equations for inelastic Maxwell models of granular gases. Phys. Rev. E 89 (5), 052201.Google Scholar
Kogan, M. K. 1969 Rarefied Gas Dynamics. Plenum.Google Scholar
Lofthouse, A. J., Boyd, I. D. & Wright, M. J. 2007 Effects of continuum breakdown on hypersonic aerothermodynamics. Phys. Fluids 19 (2), 027105.Google Scholar
Macrossan, M. N. 2007 Scaling parameters for hypersonic flow: correlation of sphere drag data. In 25th International Symposium on Rarefied Gas Dynamics, St Petersburg, Russia, pp. 759–764.Google Scholar
Matting, F. W.1964 General solution of the laminar compressible boundary layer in the stagnation region of blunt bodies in axisymmetric flow. NASA Tech. Rep. No. D-2234.Google Scholar
Nomura, S. 1983 Correlation of hypersonic stagnation point heat transfer at low Reynolds numbers. AIAA J. 21 (11), 1598–1600.Google Scholar
Nonaka, S., Mizuno, H., Takayama, K. & Park, C. 2000 Measurement of shock standoff distance for sphere in ballistic range. J. Thermophys. Heat Transfer 14 (2), 225–229.Google Scholar
Rahimi, B. & Struchtrup, H. 2014 Capturing non-equilibrium phenomena in rarefied polyatomic gases: a high-order macroscopic model. Phys. Fluids 26 (5), 052001.CrossRefGoogle Scholar
Rana, A., Torrilhon, M. & Struchtrup, H. 2013 A robust numerical method for the r13 equations of rarefied gas dynamics: application to lid driven cavity. J. Comput. Phys. 236, 169–186.Google Scholar
Schwartzentruber, T. E., Scalabrin, L. C. & Boyd, I. D. 2008a Hybrid particle–continuum simulations of hypersonic flow over a hollow-cylinder-flare geometry. AIAA J. 46 (8), 2086–2095.Google Scholar
Schwartzentruber, T. E., Scalabrin, L. C. & Boyd, I. D. 2008b Hybrid particle–continuum simulations of nonequilibrium hypersonic blunt-body flowfields. J. Thermophys. Heat Transfer 22 (1), 29–37.Google Scholar
Schwartzentruber, T. E., Scalabrin, L. C. & Boyd, I. D. 2008c Multiscale particle–continuum simulations of hypersonic flow over a planetary probe. J. Spacecr. Rockets 45 (6), 1196–1206.Google Scholar
Singh, N. & Agrawal, A. 2014 The Burnett equations in cylindrical coordinates and their solution for flow in a microtube. J. Fluid Mech. 751, 121–141.Google Scholar
Singh, N., Dongari, N. & Agrawal, A. 2013 Analytical solution of plane Poiseuille flow within Burnett hydrodynamics. Microfluid. Nanofluid. 16, 403–412.CrossRefGoogle Scholar
Singh, N., Gavasane, A. & Agrawal, A. 2014 Analytical solution of plane Couette flow in the transition regime and comparison with direct simulation Monte Carlo data. Comput. Fluids 97, 177–187.Google Scholar
Struchtrup, H. 2005 Failures of the Burnett and super-Burnett equations in steady state processes. Contin. Mech. Thermodyn. 17 (1), 43–50.Google Scholar
Struchtrup, H. & Torrilhon, M. 2003 Regularization of Grad’s 13 moment equations: derivation and linear analysis. Phys. Fluids 15 (9), 2668–2680.Google Scholar
Sutton, K. & Graves, R. Jr. 1971 A general stagnation-point convective heating equation for arbitrary gas mixtures. NASA Tech. Rep. R-376, 12–10.Google Scholar
Wang, Z., Bao, L. & Tong, B. 2010 Rarefaction criterion and non-Fourier heat transfer in hypersonic rarefied flows. Phys. Fluids 22 (12), 126103.Google Scholar
Wen, C.-Y. & Hornung, H. G. 1995 Non-equilibrium dissociating flow over spheres. J. Fluid Mech. 299, 389–405.Google Scholar
Woods, L. C. 1983 Frame-indifferent kinetic theory. J. Fluid Mech. 136, 423–433.Google Scholar
Zhao, W., Chen, W. & Agarwal, R. K. 2014 Formulation of a new set of simplified conventional Burnett equations for computation of rarefied hypersonic flows. Aerosp. Sci. Technol. 38, 64–75.Google Scholar
Zohar, Y., Lee, S. Y. K., Lee, W. Y., Jiang, L. & Tong, P. 2002 Subsonic gas flow in a straight and uniform microchannel. J. Fluid Mech. 472, 125–151.Google Scholar