Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T19:46:53.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Granular surface flows confined between flat, frictional walls. Part 1. Kinematics

Published online by Cambridge University Press:  11 April 2022

Patrick Richard Open the ORCID record for Patrick Richard [Opens in a new window] ,
Alexandre Valance Open the ORCID record for Alexandre Valance [Opens in a new window] ,
Renaud Delannay  and
Philippe Boltenhagen
Patrick Richard*
Affiliation:
Univ Gustave Eiffel, MAST-GPEM, F-44344 Bouguenais, France
Alexandre Valance
Affiliation:
IPR, Université de Rennes 1, CNRS UMR 6251, Campus Beaulieu, F-35042 Rennes, France
Renaud Delannay
Affiliation:
IPR, Université de Rennes 1, CNRS UMR 6251, Campus Beaulieu, F-35042 Rennes, France
Philippe Boltenhagen
Affiliation:
IPR, Université de Rennes 1, CNRS UMR 6251, Campus Beaulieu, F-35042 Rennes, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

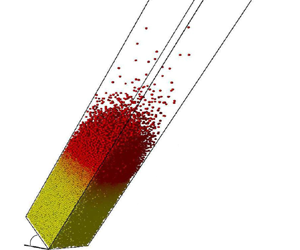
We report and analyse the results of extensive discrete element method simulations of three-dimensional gravity driven flows of cohesionless granular media over an erodible bed, the whole being confined between two flat and frictional sidewalls. We focus on the role of sidewalls by performing simulations for different gap widths ($W$) between the two confining sidewalls: from $5$ to $30$ grain sizes ($d$). Our results indicate the existence of two distinct regimes: regime I for flow angles smaller than the critical angle $\theta_c\approx 40^\circ$ and regime II at flow angles larger than $\theta_c$. Regime I corresponds to dense flows whereas flows belonging to regime II exhibit a strong variation of the volume fraction through the depth. Three relevant lengths are identified in the system: $W$ the gap between sidewalls, $l$ the length characterizing the vertical variation of the volume fraction and $h$ a characteristic length associated with the vertical variation of the streamwise velocity. Using these lengths we can rescale the profiles of various flow properties (e.g. streamwise velocity, granular temperature, particle rotation…). In regime II, in contrast to regime I, $l$ and $h$ have a similar behaviour. As a consequence, the rescaled profiles in regime II only involve $h$ (or equivalently $l$) and $W$. Other dissimilarities exist between regimes I and II. In particular, the scaling of the flow rate with $h$ (at fixed $W$) differs in the two regimes, although they display a similar scaling with $W$ (at fixed flow angle).

JFM classification

Granular media: Dry granular material Granular media: Avalanches
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 940 , 10 June 2022 , A30
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Artoni, R. & Richard, P. 2015 a Average balance equations, scale dependence, and energy cascade for granular materials. Phys. Rev. E 91, 032202.CrossRefGoogle ScholarPubMed
Artoni, R. & Richard, P. 2015 b Effective wall friction in wall-bounded 3D dense granular flows. Phys. Rev. Lett. 115, 158001.CrossRefGoogle ScholarPubMed
Artoni, R., Soligo, A., Paul, J.-M. & Richard, P. 2018 Shear localization and wall friction in confined dense granular flows. J. Fluid Mech. 849, 395–418.CrossRefGoogle Scholar
Azanza, E., Chevoir, F. & Moucheront, P. 1999 Experimental study of collisional granular flows down an inclined plane. J. Fluid Mech. 400, 199–227.CrossRefGoogle Scholar
Berzi, D., Jenkins, J.T. & Richard, P. 2019 Erodible, granular beds are fragile. Soft Matt. 15, 7173–7178.CrossRefGoogle ScholarPubMed
Bi, W., Delannay, R., Richard, P., Taberlet, N. & Valance, A. 2005 Two- and three-dimensional confined granular chute flows: experimental and numerical results. J. Phys.: Condens. Matter 17 (24), S2457–S2480.Google Scholar
Bi, W., Delannay, R., Richard, P. & Valance, A. 2006 Experimental study of two-dimensional, monodisperse, frictional-collisional granular flows down an inclined chute. Phys. Fluids 18 (12), 123302.CrossRefGoogle Scholar
Boltenhagen, P. 1999 Boundary effects on the maximal angle of stability of a granular packing. Eur. Phys. J. B 12, 75–78.CrossRefGoogle Scholar
Brodu, N., Delannay, R., Valance, A. & Richard, P. 2015 New patterns in high-speed granular flows. J. Fluid Mech. 769, 218–228.CrossRefGoogle Scholar
Brodu, N., Richard, P. & Delannay, R. 2013 Shallow granular flows down flat frictional channels: steady flows and longitudinal vortices. Phys. Rev. E 87, 022202.CrossRefGoogle ScholarPubMed
Brown, R.L. & Hawksley, P.G.W. 1946 Effect of container walls on packing density of particles.Nature (London) 157, 585.CrossRefGoogle Scholar
Bureau, L., Baumberger, T. & Caroli, C. 2002 Rheological aging and rejuvenation in solid friction contacts. Eur. Phys. J. E 8, 331–337.CrossRefGoogle ScholarPubMed
Camenen, J.-F., Descantes, Y. & Richard, P. 2012 Effect of confinement on dense packings of rigid frictionless spheres and polyhedra. Phys. Rev. E 86, 061317.CrossRefGoogle ScholarPubMed
Courrech du Pont, S., Fischer, R., Gondret, P., Perrin, B. & Rabaud, M. 2005 Instantaneous velocity profiles during granular avalanches. Phys. Rev. Lett. 94, 048003.CrossRefGoogle Scholar
Courrech du Pont, S., Gondret, P., Perrin, B. & Rabaud, M. 2003 Wall effects on granular heap stability. Europhys. Lett. 61 (4), 492.CrossRefGoogle Scholar
Crassous, J., Metayer, J.-F., Richard, P. & Laroche, C. 2008 Experimental study of a creeping granular flow at very low velocity. J. Stat. Mech. 2008 (3), P03009.CrossRefGoogle Scholar
Delannay, R., Louge, M., Richard, P., Taberlet, N. & Valance, A. 2007 Towards a theoretical picture of dense granular flows down inclines. Nat. Mater. 6, 99–108.CrossRefGoogle ScholarPubMed
Glasser, B.J. & Goldhirsch, I. 2001 Scale dependence, correlations, and fluctuations of stresses in rapid granular flows. Phys. Fluids 13 (2), 407–420.CrossRefGoogle Scholar
Haff, P.K. 1986 A physical picture of kinetic granular fluids. J. Rheol. 30 (5), 931–948.CrossRefGoogle Scholar
Hill, K.M. & Zhang, J. 2008 Kinematics of densely flowing granular mixtures. Phys. Rev. E 77, 061303.CrossRefGoogle ScholarPubMed
Hirshfeld, D. & Rapaport, D.C. 2001 Granular flow from a silo: discrete-particle simulations in three dimensions. Eur. Phys. J. E 4 (2), 193–199.CrossRefGoogle Scholar
Holyoake, A.J. & McElwaine, J.N. 2012 High-speed granular chute flows. J. Fluid Mech. 710, 35–71.CrossRefGoogle Scholar
Jenkins, J. 2007 Dense inclined flows of inelastic spheres. Granul. Matt. 10, 47–52.CrossRefGoogle Scholar
Jenkins, J.T. & Richman, M.W. 1985 Kinetic theory for plane flows of a dense gas of identical, rough, inelastic, circular disks. Phys. Fluids 28 (12), 3485–3494.CrossRefGoogle Scholar
Ji, S. & Shen, H.H. 2008 Internal parameters and regime map for soft polydispersed granular materials. J. Rheol. 52 (1), 87–103.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2005 Crucial role of sidewalls in granular surface flows: consequences for the rheology. J. Fluid Mech. 541, 167–192.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441, 727–730.CrossRefGoogle ScholarPubMed
Kamrin, K. & Henann, D.L. 2015 Nonlocal modeling of granular flows down inclines. Soft Matt. 11, 179–185.CrossRefGoogle ScholarPubMed
Khakhar, D.V., Orpe, A.V., Andresén, P. & Ottino, J.M. 2001 Surface flow of granular materials: model and experiments in heap formation. J. Fluid Mech. 441, 255–264.CrossRefGoogle Scholar
Khidas, Y., Schliecker, G., Ammi, M., Messager, J.-C. & Delannay, R. 2000 Rotational modes in a 1d array of cylinders under shear stress. Europhys. Lett. 50 (5), 587.CrossRefGoogle Scholar
Komatsu, T.S., Inagaki, S., Nakagawa, N. & Nasuno, S. 2001 Creep motion in a granular pile exhibiting steady surface flow. Phys. Rev. Lett. 86 (9), 1757–1760.CrossRefGoogle Scholar
Lemieux, P.-A. & Durian, D.J. 2000 From avalanches to fluid flow: a continuous picture of grain dynamics down a heap. Phys. Rev. Lett. 85 (20), 4273–4276.CrossRefGoogle Scholar
Li, L. & Andrade, J.E. 2020 Identifying spatial transitions in heterogenous granular flow. Granul. Matt. 22, 52.CrossRefGoogle Scholar
Liu, C.-H., Jaeger, H.M. & Nagel, S.R. 1991 Finite-size effects in a sandpile. Phys. Rev. A 43 (12), 7091–7092.CrossRefGoogle Scholar
Losert, W., Bocquet, L., Lubensky, T.C. & Gollub, J.P. 2000 Particle dynamics in sheared granular matter. Phys. Rev. Lett. 85, 1428–1431.CrossRefGoogle ScholarPubMed
Louge, M.Y. 2003 Model for dense granular flows down bumpy inclines. Phys. Rev. E 67, 061303.CrossRefGoogle ScholarPubMed
Lun, C.K. & Savage, S.B. 1987 A simple kinetic theory for granular flow of rough, inelastic, spherical particles. Trans. ASME J. Appl. Mech. 54, 47–53.CrossRefGoogle Scholar
Martínez, E., González-Lezcano, A., Batista-Leyva, A.J. & Altshuler, E. 2016 Exponential velocity profile of granular flows down a confined heap. Phys. Rev. E 93, 062906.CrossRefGoogle Scholar
Metayer, J.-F., Richard, P., Faisant, A. & Delannay, R. 2010 Electrically induced tunable cohesion in granular systems. J. Stat. Mech. 2010 (08), P08003.CrossRefGoogle Scholar
Mueth, D.M. 2003 Measurements of particle dynamics in slow, dense granular Couette flow. Phys. Rev. E 67, 011304.CrossRefGoogle ScholarPubMed
Orpe, A.V. & Khakhar, D.V. 2007 Rheology of surface granular flows. J. Fluid Mech. 571, 1–32.CrossRefGoogle Scholar
Radjai, F., Brendel, L. & Roux, S. 1996 Nonsmoothness, indeterminacy, and friction in two-dimensional arrays of rigid particles. Phys. Rev. E 54, 861–873.CrossRefGoogle ScholarPubMed
Richard, P., Artoni, R., Valance, A. & Delannay, R. 2020 Influence of lateral confinement on granular flows: comparison between shear-driven and gravity-driven flows. Granul. Matt. 22, 81.CrossRefGoogle Scholar
Richard, P., McNamara, S. & Tankeo, M. 2012 Relevance of numerical simulations to booming sand. Phys. Rev. E 85, 010301.CrossRefGoogle ScholarPubMed
Richard, P. & Taberlet, N. 2008 Recent advances in DEM simulations of grains in a rotating drum. Soft Matt. 4, 1345–1348.CrossRefGoogle Scholar
Richard, P., Valance, A., Métayer, J.-F., Crassous, J., Louge, M. & Delannay, R. 2010 Rheology of confined granular flows. AIP Conf. Proc. 1227 (1), 79–88.CrossRefGoogle Scholar
Richard, P., Valance, A., Métayer, J.-F., Sanchez, P., Crassous, J., Louge, M. & Delannay, R. 2008 Rheology of confined granular flows: scale invariance, glass transition, and friction weakening. Phys. Rev. Lett. 101 (24), 248002.CrossRefGoogle ScholarPubMed
de Ryck, A., Zhu, H.P., Wu, S.M., Yu, A.B. & Zulli, P. 2010 Numerical and theoretical investigation of the surface flows of granular materials on heaps. Powder Technol. 203 (2), 125–132.CrossRefGoogle Scholar
Rycroft, C.H., Orpe, A.V. & Kudrolli, A. 2009 Physical test of a particle simulation model in a sheared granular system. Phys. Rev. E 80 (3), 031305.CrossRefGoogle Scholar
Silbert, L.E., Ertaş, D., Grest, G.S., Halsey, T.C., Levine, D. & Plimpton, S.J. 2001 Granular flow down an inclined plane: Bagnold scaling and rheology. Phys. Rev. E 64 (5), 051302.CrossRefGoogle ScholarPubMed
Taberlet, N., Newey, M., Richard, P. & Losert, W. 2006 a On axial segregation in a tumbler: an experimental and numerical study. J. Stat. Mech. 2006 (07), P07013.CrossRefGoogle Scholar
Taberlet, N., Richard, P. & Delannay, R. 2008 The effect of sidewall friction on dense granular flows. Comput. Maths Applics. 55 (2), 230–234.CrossRefGoogle Scholar
Taberlet, N., Richard, P., Henry, E. & Delannay, R. 2004 The growth of a super stable heap: an experimental and numerical study. Europhys. Lett. 68 (4), 515–521.CrossRefGoogle Scholar
Taberlet, N., Richard, P. & John Hinch, E. 2006 b $s$ shape of a granular pile in a rotating drum. Phys. Rev. E 73 (5), 050301.CrossRefGoogle Scholar
Taberlet, N., Richard, P., Valance, A., Losert, W., Pasini, J.M., Jenkins, J.T. & Delannay, R. 2003 Superstable granular heap in a thin channel. Phys. Rev. Lett. 91 (26), 264301.CrossRefGoogle Scholar
Verman, L.C. & Banerjee, S. 1946 Effect of container walls on packing density of particles. Nature 157, 584–585.CrossRefGoogle Scholar
Vescovi, D., Berzi, D. & di Prisco, C. 2018 Fluid–solid transition in unsteady, homogeneous, granular shear flows. Granul. Matt. 20 (2), 27.CrossRefGoogle Scholar
Vescovi, D. & Luding, S. 2016 Merging fluid and solid granular behavior. Soft Matt. 12, 8616–8628.CrossRefGoogle ScholarPubMed
Xu, H., Reeves, A.P. & Louge, M.Y. 2004 Measurement errors in the mean and fluctuation velocities of spherical grains from a computer analysis of digital images. Rev. Sci. Instrum. 75 (4), 811–819.CrossRefGoogle Scholar
Yang, F.-L. & Huang, Y.-T. 2016 New aspects for friction coefficients of finite granular avalanche down a flat narrow reservoir. Granul. Matt. 18 (4), 77.CrossRefGoogle Scholar
Zhang, S., Yang, G., Lin, P., Chen, L. & Yang, L. 2019 Inclined granular flow in a narrow chute. Eur. Phys. J. E 42 (4), 40.CrossRefGoogle Scholar
Zhu, Y., Delannay, R. & Valance, A. 2020 High-speed confined granular flows down smooth inclines: scaling and wall friction laws. Granul. Matt. 22, 82.CrossRefGoogle Scholar