Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T07:36:39.491Z Has data issue: false hasContentIssue false
  • English
  • Français

Görtler vortices in low-Reynolds-number flow over multi-element airfoil

Published online by Cambridge University Press:  28 November 2017

Jiang-Sheng Wang ,
Li-Hao Feng Open the ORCID record for Li-Hao Feng [Opens in a new window] ,
Jin-jun Wang Open the ORCID record for Jin-jun Wang [Opens in a new window]  and
Tian Li
Jiang-Sheng Wang
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Li-Hao Feng
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Jin-jun Wang*
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Tian Li
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China Shenyang Aircraft Design and Research Institute, Shenyang 110035, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The low-Reynolds-number flow over a multi-element airfoil (30P30N) is investigated with time-resolved particle image velocimetry (TR-PIV) and flow visualization (FV). Dominant flow structures over the main element of the multi-element airfoil are explored with the variation of angle of attack ($\unicode[STIX]{x1D6FC}$). It is of great importance that Görtler vortices are first observed with this configuration at 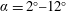$\unicode[STIX]{x1D6FC}=2^{\circ }{-}12^{\circ }$, which is quite different from the high-Reynolds-number cases. The characteristics of the Görtler vortices are explored to determine the origin of these unexpected flow structures. It is found that these Görtler vortices travel in the spanwise direction. Secondary counter-rotating vortices are induced beneath the main Görtler vortices. The travelling property of the Görtler vortices is utilized to determine the positions of the main Görtler vortices and the secondary counter-rotating vortices. It is observed that Görtler vortices reside above the separated shear layer originating from the leading-edge separation of the main element. The secondary counter-rotating vortices are located within the separated shear layer, as a result of the interaction between the Görtler vortices and the separated shear layer. The relative positions of the Görtler vortices, the secondary counter-rotating vortices and the separated shear layer result in a special transition scenario within the separated shear layer. The position of Görtler vortices combined with the Rayleigh discriminant indicates the mechanism that the Görtler vortices are generated by a virtual curved boundary. The travelling property of the Görtler vortices, which is different from the classical stationary Görtler vortices, can also be interpreted by this mechanism. Ultimately, modified criteria for generating Görtler vortices with a virtual curved boundary are proposed to provide references for the follow-up works.

JFM classification

Aerodynamics: Aerodynamics Instability: Instability Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 835 , 25 January 2018 , pp. 898 - 935
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D., Gomes, M. G. M. & Henderson, R. D. 2002 Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 473, 167–190.Google Scholar
Beaudoin, J.-F., Cadot, O., Aider, J.-L. & Wesfreid, J. E. 2004 Three-dimensional stationary flow over a backward-facing step. Eur. J. Mech. (B/Fluids) 23 (1), 147–155.CrossRefGoogle Scholar
Benmalek, A. & Saric, W. S. 1994 Effects of curvature variations on the nonlinear evolution of goertler vortices. Phys. Fluids 6 (10), 3353–3367.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.Google Scholar
Boutilier, M. S. & Yarusevych, S. 2012a Effects of end plates and blockage on low-Reynolds-number flows over airfoils. AIAA J. 50 (7), 1547–1559.Google Scholar
Boutilier, M. S. H. & Yarusevych, S. 2012b Separated shear layer transition over an airfoil at a low Reynolds number. Phys. Fluids 24 (8), 084105.Google Scholar
Brinkerhoff, J. R. & Yaras, M. I. 2015 Numerical investigation of transition in a boundary layer subjected to favourable and adverse streamwise pressure gradients and elevated free stream turbulence. J. Fluid Mech. 781, 52–86.Google Scholar
Burgmann, S. & Schröder, W. 2008 investigation of the vortex induced unsteadiness of a separation bubble via time-resolved and scanning piv measurements. Exp. Fluids 45 (4), 675–691.Google Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.Google Scholar
Carmichael, B. 1981 Low Reynolds Number Airfoil Survey, vol. 1. NASA Technical Report, NASA-CR-165803.Google Scholar
Champagnat, F., Plyer, A., Le Besnerais, G., Leclaire, B., Davoust, S. & Le Sant, Y. 2011 Fast and accurate piv computation using highly parallel iterative correlation maximization. Exp. Fluids 50 (4), 1169–1182.CrossRefGoogle Scholar
Chatterjee, A. 2000 An introduction to the proper orthogonal decomposition. Curr. Sci. 78 (7), 808–817.Google Scholar
Choudhari, M. & Lockard, D. P. 2015 Assessment of slat noise predictions for 30p30n high-lift configuration from banc-Iii workshop. In 21st AIAA/CEAS Aeroacoustics Conference, AIAA AVIATION Forum, AIAA Paper 2015-2844.Google Scholar
Choudhari, M. M. & Khorrami, M. R.2006 Slat cove unsteadiness: effect of 3d flow structures. AIAA Paper 2006-211.Google Scholar
Choudhari, M. M. & Khorrami, M. R. 2007 Effect of three-dimensional shear-layer structures on slat cove unsteadiness. AIAA J. 45 (9), 2174–2186.Google Scholar
Choudhari, M. M. & Yamamoto, K.2012 Integrating Cfd, Caa, and experiments towards benchmark datasets for airframe noise problems. NASA Conference Paper NF-1676L-14832.Google Scholar
Christensen, K. 2004 The influence of peak-locking errors on turbulence statistics computed from piv ensembles. Exp. Fluids 36 (3), 484–497.Google Scholar
Christensen, K. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.Google Scholar
Deck, S. & Laraufie, R. 2013 Numerical investigation of the flow dynamics past a three-element aerofoil. J. Fluid Mech. 732, 401–444.Google Scholar
Dobrzynski, W. 2010 Almost 40 years of airframe noise research: what did we achieve? J. Aircraft 47 (2), 353–367.Google Scholar
Douay, C., Pastur, L. & Lusseyran, F. 2016a Centrifugal instabilities in an experimental open cavity flow. J. Fluid Mech. 788, 670–694.Google Scholar
Douay, C. L., Lusseyran, F. & Pastur, L. R. 2016b The onset of centrifugal instability in an open cavity flow. Fluid Dyn. Res. 48 (6), 061410.Google Scholar
Faure, T. M. 2014 Velocity field and parametric analysis of a subsonic, medium-Reynolds number cavity flow. Exp. Fluids 55 (11), 1–18.Google Scholar
Faure, T. M., Adrianos, P., Lusseyran, F. & Pastur, L. 2007 Visualizations of the flow inside an open cavity at medium range Reynolds numbers. Exp. Fluids 42 (2), 169–184.CrossRefGoogle Scholar
Faure, T. M., Pastur, L., Lusseyran, F., Fraigneau, Y. & Bisch, D. 2009 Three-dimensional centrifugal instabilities development inside a parallelepipedic open cavity of various shape. Exp. Fluids 47 (3), 395–410.Google Scholar
Finnis, M. & Brown, A. 1997 The linear growth of Görtler vortices. Intl J. Heat Fluid Flow 18 (4), 389–399.Google Scholar
Floryan, J. 1991 On the Görtler instability of boundary layers. Prog. Aerosp. Sci. 28 (3), 235–271.CrossRefGoogle Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Gaster, M. 1969 The Structure and Behaviour of Laminar Separation Bubbles. Citeseer.Google Scholar
Green, M., Rowley, C. & Haller, G. 2007 Detection of Lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 572, 111–120.Google Scholar
Hain, R., Kähler, C. & Radespiel, R. 2009 Dynamics of laminar separation bubbles at low-Reynolds-number aerofoils. J. Fluid Mech. 630, 129–153.Google Scholar
Haines, A.1994 Scale effects on aircraft and weapon aerodynamics (Les Effets D’echelle Et L’aerodynamique Des Aeronefs Et Des Systemes D’armes), DTIC Document.Google Scholar
Haller, G. 2001 Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Physica D 149 (4), 248–277.Google Scholar
Haller, G. & Yuan, G. 2000 Lagrangian coherent structures and mixing in two-dimensional turbulence. Physica D 147 (3), 352–370.Google Scholar
Hansen, H., Thiede, P., Moens, F., Rudnik, R. & Quest, J.2004 Overview about the European high lift research programme eurolift. AIAA Paper 2004-767.Google Scholar
He, G.-S., Pan, C., Feng, L.-H., Gao, Q. & Wang, J.-J. 2016 Evolution of Lagrangian coherent structures in a cylinder-wake disturbed flat plate boundary layer. J. Fluid Mech. 792, 274–306.Google Scholar
Inger, G.1987 Spanwise-periodic three-dimensional disturbances in the wake of a slightly stalled wing. AIAA Paper 87:0456.Google Scholar
Jenkins, L. N., Khorrami, M. R. & Choudhari, M.2004 Characterization of unsteady flow structures near leading-edge slat. Part I. Piv measurements. AIAA Paper 2004-2801.CrossRefGoogle Scholar
Jones, L., Sandberg, R. & Sandham, N. 2008 Direct numerical simulations of forced and unforced separation bubbles on an airfoil at incidence. J. Fluid Mech. 602, 175–207.Google Scholar
Kurelek, J. W., Lambert, A. R. & Yarusevych, S. 2016 Coherent structures in the transition process of a laminar separation bubble. AIAA J. 54 (8), 2295–2309.Google Scholar
Lang, M., Rist, U. & Wagner, S. 2004 Investigations on controlled transition development in a laminar separation bubble by means of lda and piv. Exp. Fluids 36 (1), 43–52.Google Scholar
Lengani, D. & Simoni, D. 2015 Recognition of coherent structures in the boundary layer of a low-pressure-turbine blade for different free-stream turbulence intensity levels. Intl J. Heat Fluid Flow 54, 1–13.Google Scholar
Lengani, D., Simoni, D., Ubaldi, M. & Zunino, P. 2014 Pod analysis of the unsteady behavior of a laminar separation bubble. Exp. Therm. Fluid Sci. 58, 70–79.Google Scholar
Lengani, D., Simoni, D., Ubaldi, M., Zunino, P. & Bertini, F. 2017 Experimental study of free-stream turbulence induced transition in an adverse pressure gradient. Exp. Therm. Fluid Sci. 84, 18–27.Google Scholar
Ligrani, P. M. & Niver, R. D. 1988 Flow visualization of dean vortices in a curved channel with 40 to 1 aspect ratio. Phys. Fluids 31 (12), 3605–3617.Google Scholar
Lissaman, P. 1983 Low-Reynolds-number airfoils. Annu. Rev. Fluid Mech. 15 (1), 223–239.Google Scholar
Lockard, D. P., Choudhari, M. M. & Buning, P. G. 2015 Influence of spanwise boundary conditions on slat noise simulations. In 21st AIAA/CEAS Aeroacoustics Conference, AIAA AVIATION Forum, AIAA Paper 2015-3136.Google Scholar
Ma, L., Feng, L., Pan, C., Gao, Q. & Wang, J. 2015 Fourier mode decomposition of piv data. Sci. China Technol. Sci. 58 (11), 1935–1948.Google Scholar
Makiya, S., Inasawa, A. & Asai, M. 2010 Vortex shedding and noise radiation from a slat trailing edge. AIAA J. 48 (2), 502–509.Google Scholar
Mandal, A., Venkatakrishnan, L. & Dey, J. 2010 A study on boundary-layer transition induced by free-stream turbulence. J. Fluid Mech. 660, 114–146.Google Scholar
Mandal, A. C. & Dey, J. 2011 An experimental study of boundary layer transition induced by a cylinder wake. J. Fluid Mech. 684, 60–84.Google Scholar
Marxen, O. & Henningson, D. S. 2011 The effect of small-amplitude convective disturbances on the size and bursting of a laminar separation bubble. J. Fluid Mech. 671, 1–33.Google Scholar
Marxen, O., Lang, M. & Rist, U. 2013 Vortex formation and vortex breakup in a laminar separation bubble. J. Fluid Mech. 728, 58–90.CrossRefGoogle Scholar
Marxen, O., Lang, M., Rist, U., Levin, O. & Henningson, D. S. 2009 Mechanisms for spatial steady three-dimensional disturbance growth in a non-parallel and separating boundary layer. J. Fluid Mech. 634, 165–189.Google Scholar
Matsubara, M. & Alfredsson, P. H. 2001 Disturbance growth in boundary layers subjected to free-stream turbulence. J. Fluid Mech. 430, 149–168.Google Scholar
Mcauliffe, B. R. & Yaras, M. I. 2009 Transition mechanisms in separation bubbles under low- and elevated-freestream turbulence. Trans. ASME J. Turbomach. 132 (1), 011004.Google Scholar
Meyer, M., Hickel, S., Breitsamter, C. & Adams, N.2013 Wall-modelled implicit large-eddy simulation of the Ra16sc1 highlift configuration. AIAA Paper 2014-3037.Google Scholar
Mueller, T. J. & Delaurier, J. D. 2003 Aerodynamics of small vehicles. Annu. Rev. Fluid Mech. 35 (1), 89–111.Google Scholar
Pan, C., Xue, D., Xu, Y., Wang, J. & Wei, R. 2015 Evaluating the accuracy performance of Lucas–Kanade algorithm in the circumstance of piv application. Sci. China Phys. Mech. Astron. 58 (10), 1–16.Google Scholar
Paschal, K., Jenkins, L. & Yao, C.2000 Unsteady slat-wake characteristics of a high-lift configuration. AIAA Paper 2000-139.Google Scholar
Saric, W. S. 1994 Goumlrtler vortices. Annu. Rev. Fluid Mech. 26 (1), 379–409.Google Scholar
Scarano, F. & Riethmuller, M. L. 2000 Advances in iterative multigrid piv image processing. Exp. Fluids 29, S051–S060.Google Scholar
Schlatter, P., Brandt, L., De Lange, H. & Henningson, D. S. 2008 On streak breakdown in bypass transition. Phys. Fluids 20 (10), 101505.Google Scholar
Shadden, S. C., Astorino, M. & Gerbeau, J.-F. 2010 Computational analysis of an aortic valve jet with Lagrangian coherent structures. Chaos 20 (1), 017512.Google Scholar
Shadden, S. C., Dabiri, J. O. & Marsden, J. E. 2006 Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids 18 (4), 047105.CrossRefGoogle Scholar
Shadden, S. C., Lekien, F. & Marsden, J. E. 2005 Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D 212 (3–4), 271–304.Google Scholar
Simoni, D., Ubaldi, M., Zunino, P., Lengani, D. & Bertini, F. 2012 An experimental investigation of the separated-flow transition under high-lift turbine blade pressure gradients. Flow Turbul. Combust. 88 (1), 45–62.Google Scholar
Simpson, R. L. 1989 Turbulent boundary-layer separation. Annu. Rev. Fluid Mech. 21 (1), 205–232.Google Scholar
Sipp, D. & Jacquin, L. 2000 A criterion of centrifugal instabilities in rotating systems. In Vortex Structure and Dynamics, pp. 299–308. Springer.Google Scholar
Souza, D. S., Rodríguez, D., Simões, L. G. C. & Medeiros, M. a. F. 2015 Effect of an excrescence in the slat cove: flow-field, acoustic radiation and coherent structures. Aerosp. Sci. Technol. 44, 108–115.Google Scholar
Swearingen, J. D. & Blackwelder, R. F. 1987 The growth and breakdown of streamwise vortices in the presence of a wall. J. Fluid Mech. 182, 255–290.Google Scholar
Terracol, M., Manoha, E., Murayama, M., Yamamoto, K., Amemiya, K. & Tanaka, K. 2015 Aeroacoustic calculations of the 30p30n high-lift airfoil using hybrid rans/les methods: modeling and grid resolution effects. In 21st AIAA/CEAS Aeroacoustics Conference.Google Scholar
Van Dam, C. 2002 The aerodynamic design of multi-element high-lift systems for transport airplanes. Prog. Aerosp. Sci. 38 (2), 101–144.Google Scholar
Wang, J., Pan, C., Choi, K.-S., Gao, L. & Lian, Q.-X. 2013 Formation, growth and instability of vortex pairs in an axisymmetric stagnation flow. J. Fluid Mech. 725, 681–708.Google Scholar
Wang, S., Zhou, Y., Alam, M. M. & Yang, H. 2014 Turbulent intensity and Reynolds number effects on an airfoil at low Reynolds numbers. Phys. Fluids 26 (11), 115107.Google Scholar
Watmuff, J. H. 1999 Evolution of a wave packet into vortex loops in a laminar separation bubble. J. Fluid Mech. 397 (1), 119–169.Google Scholar
Williamson, C. H. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.Google Scholar
Winoto, S., Mitsudharmadi, H. & Shah, D. A. 2005 Visualizing Görtler vortices. J. Vis. 8 (4), 315–322.Google Scholar
Winoto, S. & Shah, D. 2008 On the linear and nonlinear development of Görtler vortices. Phys. Fluids 20 (9), 094103.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar