Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T07:53:09.096Z Has data issue: false hasContentIssue false
  • English
  • Français

Global stability of buoyant jets and plumes

Published online by Cambridge University Press:  27 November 2017

R. V. K. Chakravarthy ,
L. Lesshafft Open the ORCID record for L. Lesshafft [Opens in a new window]  and
P. Huerre
R. V. K. Chakravarthy
Affiliation:
Laboratoire d’Hydrodynamique, CNRS/École Polytechnique 91128 Palaiseau, France
L. Lesshafft*
Affiliation:
Laboratoire d’Hydrodynamique, CNRS/École Polytechnique 91128 Palaiseau, France
P. Huerre
Affiliation:
Laboratoire d’Hydrodynamique, CNRS/École Polytechnique 91128 Palaiseau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

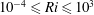The linear global stability of laminar buoyant jets and plumes is investigated under the low-Mach-number approximation. For Richardson numbers in the range $10^{-4}\leqslant Ri\leqslant 10^{3}$ and density ratios 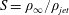$S=\unicode[STIX]{x1D70C}_{\infty }/\unicode[STIX]{x1D70C}_{jet}$ between 1.05 and 7, only axisymmetric perturbations are found to exhibit global instability, consistent with experimental observations in helium jets. By varying the Richardson number over seven decades, the effects of buoyancy on the base flow and on the instability dynamics are characterised, and distinct behaviour is observed in the low-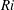$Ri$ (jet) and in the high-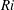$Ri$ (plume) regimes. A sensitivity analysis indicates that different physical mechanisms are responsible for the global instability dynamics in both regimes. In buoyant jets at low Richardson number, the baroclinic torque enhances the basic shear instability, whereas buoyancy provides the dominant instability mechanism in plumes at high Richardson number. The onset of axisymmetric global instability in both regimes is consistent with the presence of absolute instability. While absolute instability also occurs for helical perturbations, it appears to be too weak or too localised to give rise to a global instability.

JFM classification

Convection: Buoyancy-driven instability Wakes/Jets: Jets Convection: Plumes/thermals
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 835 , 25 January 2018 , pp. 654 - 673
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Ehrenstein, U., Gallaire, F. & Henningson, D. 2008 Global two-dimensional stability measures of the flat plate boundary-layer flow. Eur. J. Mech. (B/Fluids) 27, 1–13.Google Scholar
Bharadwaj, K. & Das, D. 2017 Global instability analysis and experiments of buoyant plumes. J. Fluid Mech. 832, 97–145.Google Scholar
Boujemaa, S., Amielh, M. & Chauve, M. P. 2004 Analyse spatio-temporelle de jets axisymétriques d’air et d’hélium. C. R. Méc. 332 (11), 933–939.CrossRefGoogle Scholar
Cetegen, B. M. & Kasper, K. D. 1996 Experiments on the oscillatory behavior of buoyant plumes of helium and helium-air mixtures. Phys. Fluids 8 (11), 2974–2984.Google Scholar
Chakravarthy, R. V. K.2015 Local and global instabilities in buoyant jets and plumes. PhD thesis, École Polytechnique, Palaiseau, France.Google Scholar
Chakravarthy, R. V. K., Lesshafft, L. & Huerre, P. 2015 Local linear stability of laminar axisymmetric plumes. J. Fluid Mech. 780, 344–369.Google Scholar
Chandler, G. J.2010 Sensitivity analysis of low density jets and flames. PhD thesis, University of Cambridge, Cambridge, UK.Google Scholar
Chomaz, J.-M. 2003 Fully nonlinear dynamics of parallel wakes. J. Fluid Mech. 495, 57–75.Google Scholar
Chomaz, J. M., Huerre, P. & Redekopp, L. G. 1991 A frequency selection criterion in spatially developing flows. Stud. Appl. Maths 84 (2), 119–144.Google Scholar
Coenen, W., Lesshafft, L., Garnaud, X. & Sevilla, A. 2017 Global instability of low-density jets. J. Fluid Mech. 820, 187–207.CrossRefGoogle Scholar
Colonius, T. 2004 Modeling artificial boundary conditions for compressible flow. Annu. Rev. Fluid Mech. 36, 315–345.Google Scholar
Couairon, A. & Chomaz, J. M. 1997 Absolute and convective instabilities, front velocities and global modes in nonlinear systems. Physica D: Nonlinear Phenomena. 108 (3), 236–276.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013 Modal and transient dynamics of jet flows. Phys. Fluids 25 (4), 044103.Google Scholar
Hallberg, M. P. & Strykowski, P. J. 2006 On the universality of global modes in low-density axisymmetric jets. J. Fluid Mech. 569, 493–507.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.Google Scholar
Jiang, X. & Luo, K. H. 2000 Direct numerical simulation of the puffing phenomenon of an axisymmetric thermal plume. Theor. Comput. Fluid Dyn. 14, 55–74.Google Scholar
Khorrami, M. R., Malik, M. R. & Ash, R. L. 1989 Application of spectral collocation techniques to the stability of swirling flows. J. Comput. Phys. 81, 206–229.CrossRefGoogle Scholar
Lakkaraju, R. & Alam, M. 2007 Effects of Prandtl number and a new instability mode in a plane thermal plume. J. Fluid Mech. 592, 221–231.Google Scholar
Lesshafft, L. 2015 Linear global stability of a confined plume. Theoret. Appl. Mech. Lett. 5 (3), 126–128.Google Scholar
Lesshafft, L.2017 Artificial eigenmodes in truncated flow domains. Preprint, arXiv:1704.08450.Google Scholar
Lesshafft, L. & Huerre, P. 2007 Linear impulse response in hot round jets. Phys. Fluids 19 (2), 024102.Google Scholar
Lesshafft, L., Huerre, P. & Sagaut, P. 2007 Frequency selection in globally unstable round jets. Phys. Fluids 19, 054108.Google Scholar
Lesshafft, L., Huerre, P., Sagaut, P. & Terracol, M. 2006 Nonlinear global modes in hot jets. J. Fluid Mech. 554, 393–409.CrossRefGoogle Scholar
Lesshafft, L. & Marquet, O. 2010 Optimal velocity and density profiles for the onset of absolute instability in jets. J. Fluid Mech. 662, 398–408.Google Scholar
Lopez, J. M. & Marques, F. 2013 Instability of plumes driven by localized heating. J. Fluid Mech. 736, 616–640.Google Scholar
Marquet, O. & Lesshafft, L.2015 Identifying the active flow regions that drive linear and nonlinear instabilities. Preprint, arXiv:1508.07620.Google Scholar
McMurtry, P. A., Jou, W. H., Riley, J. J. & Metcalfe, R. W. 1986 Direct numerical simulations of a reacting mixing layer with chemical heat release. AIAA J. 24 (6), 962–970.Google Scholar
Mollendorf, J. C. & Gebhart, B. 1973 An experimental and numerical study of the viscous stability of a round laminar vertical jet with and without thermal buoyancy for symmetric and asymmetric perturbations. J. Fluid Mech. 61 (2), 367–399.Google Scholar
Monkewitz, P. A., Bechert, D. W., Barsikow, B. & Lehmann, B. 1990 Self-excited oscillations and mixing in a heated round jet. Phys. Fluids 213, 611–639.Google Scholar
Monkewitz, P. A. & Sohn, K. 1988 Absolute instability in hot jets. AIAA J. 26, 911–916.Google Scholar
Nichols, J. W., Schmid, P. J. & Riley, J. J. 2007 Self-sustained oscillations in variable-density round jets. J. Fluid Mech. 582, 341–376.CrossRefGoogle Scholar
Riley, D. S. & Tveitereid, M. 1984 On the stability of an axisymmetric plume in a uniform flow. J. Fluid Mech. 142, 171–186.Google Scholar
Satti, R. P. & Agrawal, A. K. 2006 Computational analysis of gravitational effects in low-density gas jets. AIAA 44 (7), 1505–1515.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows, Applied Mathematical Sciences, vol. 142. Springer.Google Scholar
Sreenivasan, K. R., Raghu, S. & Kyle, D. 1989 Absolute instability in variable density round jets. Exp. Fluids 213, 309–317.Google Scholar
Subbarao, E. R. & Cantwell, B. J. 1992 Investigation of a co-flowing buoyant jet: experiments on the effect of Reynolds number and Richardson number. J. Fluid Mech. 245, 69–90.Google Scholar
Theofilis, V. 2003 Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aero. Sci. 39 (4), 249–315.CrossRefGoogle Scholar
Tritton, D. J. 2012 Physical Fluid Dynamics. Springer Science & Business Media.Google Scholar
Wakitani, S. 1980 The stability of a natural convection flow above a point heat source. J. Phys. Soc. Japan 49 (6), 2392–2399.Google Scholar
Yih, C. S. 1988 Fluid Mechanics. West River Press.Google Scholar