Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T06:25:58.214Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric formulation of the Cauchy invariants for incompressible Euler flow in flat and curved spaces

Published online by Cambridge University Press:  21 July 2017

Nicolas Besse  and
Uriel Frisch Open the ORCID record for Uriel Frisch [Opens in a new window]
Nicolas Besse*
Affiliation:
Université Côte d’Azur, Observatoire de la Côte d’Azur, Nice, France
Uriel Frisch
Affiliation:
Université Côte d’Azur, Observatoire de la Côte d’Azur, Nice, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Cauchy invariants are now viewed as a powerful tool for investigating the Lagrangian structure of three-dimensional (3D) ideal flow (Frisch & Zheligovsky, Commun. Math. Phys., vol. 326, 2014, pp. 499–505; Podvigina et al., J. Comput. Phys., vol. 306, 2016, pp. 320–342). Looking at such invariants with the modern tools of differential geometry and of geodesic flow on the space SDiff of volume-preserving transformations (Arnold, Ann. Inst. Fourier, vol. 16, 1966, pp. 319–361), all manners of generalisations are here derived. The Cauchy invariants equation and the Cauchy formula, relating the vorticity and the Jacobian of the Lagrangian map, are shown to be two expressions of this Lie-advection invariance, which are duals of each other (specifically, Hodge dual). Actually, this is shown to be an instance of a general result which holds for flow both in flat (Euclidean) space and in a curved Riemannian space: any Lie-advection invariant 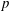$p$-form which is exact (i.e. is a differential of a 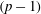$(p-1)$-form) has an associated Cauchy invariants equation and a Cauchy formula. This constitutes a new fundamental result in linear transport theory, providing a Lagrangian formulation of Lie advection for some classes of differential forms. The result has a broad applicability: examples include the magnetohydrodynamics (MHD) equations and various extensions thereof, discussed by Lingam et al. (Phys. Lett. A, vol. 380, 2016, pp. 2400–2406), and include also the equations of Tao (2016, arXiv:1606.08481 [math.AP]), Euler equations with modified Biot–Savart law, displaying finite-time blow-up. Our main result is also used for new derivations, and several new results, concerning local helicity-type invariants for fluids and MHD flow in flat or curved spaces of arbitrary dimension.

JFM classification

Mathematical Foundations: General fluid mechanics Mathematical Foundations: Mathematical Foundations Mathematical Foundations: Variational methods
Type
Papers
Information
Journal of Fluid Mechanics , Volume 825 , 25 August 2017 , pp. 412 - 478
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, R., Marsden, J. E. & Ratiu, R. 1998 Manifolds, Tensor Analysis, and Applications. Springer.Google Scholar
Abrashkin, A. A., Zen’kovich, D. A. & Yakubovich, E. I. 1996 Matrix formulation of hydrodynamics and extension of Ptolemaic flows to three-dimensional motions. Radiophys. Quantum El. 39, 518–526; Translated from Izv. Vuz. Radiofi. 39, 783–796, 1996 (in Russian).CrossRefGoogle Scholar
Alles, A., Buchert, T., Al Roumi, F. & Wiegand, A. 2015 Lagrangian theory of structure formation in relativistic cosmology. III. Gravitoelectric perturbation and solution schemes at any order. Phys. Rev. D 92, 023512.Google Scholar
Andrews, D. G. & McIntyre, M. E. 1978 An exact theory of nonlinear waves on a Lagrangian mean flow. J. Fluid Mech. 89, 609–646.CrossRefGoogle Scholar
Arnold, V. I. 1966 Sur la géometrie différentielle des groupes de Lie de dimension infinie et ses applications à l’hydrodynamique des fluides parfaits. Ann. Inst. Fourier 16, 319–361.CrossRefGoogle Scholar
Arnold, V. I. 1989 Mathematical Methods of Classical Mechanics. Springer.CrossRefGoogle Scholar
Arnold, V. I. & Khesin, B. A. 1998 Topological Methods in Hydrodynamics. Springer.Google Scholar
Besse, N. & Frisch, U. 2017 A constructive approach to regularity of Lagrangian trajectories for incompressible Euler flow in a bounded domain. Commun. Math. Phys. 351, 689–707.CrossRefGoogle Scholar
Bluman, G. W. & Anco, S. C. 2002 Symmetry and Integration Methods for Differential Equations. Springer.Google Scholar
Bluman, G. W., Cheviakov, A. F. & Anco, S. C. 2010 Application of Symmetry Methods to Partial Differential Equations. Springer.Google Scholar
Buchert, T. & Ostermann, M. 2012 Lagrangian theory of structure formation in relativistic cosmology: Lagrangian framework and definition of a nonperturbative approximation. Phys. Rev. D 86, 023520.Google Scholar
Cary, J. R. 1977 Lie transform perturbation theory for Hamiltonian systems. Phys. Rep. 79, 129–159.Google Scholar
Cauchy, A. L.1815 Sur l’état du fluide à une époque quelconque du mouvement. Mémoires extraits des recueils de l’Académie des sciences de l’Institut de France, Théorie de la propagation des ondes à la surface d’un fluide pesant d’une profondeur indéfinie (Extraits des Mémoires présentés par divers savants à l’Académie royale des Sciences de l’Institut de France et imprimés par son ordre). Sciences mathématiques et physiques. Tome I, 1827 Seconde Partie, pp. 33–73.Google Scholar
Choquet-Bruhat, Y. 1968 Géométrie différentielle et systèmes extérieurs. Dunod.Google Scholar
Choquet-Bruhat, Y. 2008 General Relativity and Einstein Equations. Oxford University Press.CrossRefGoogle Scholar
Choquet-Bruhat, Y., De Witt-Morette, C. & Dillard-Bleick, M. 1977 Analysis, Manifolds and Physics. Part 1. North-Holland.Google Scholar
Clebsch, A. 1859 Ueber die Integration der hydrodynamischen Gleichungen. J. Reine Angew. Math. 56, 1–10.Google Scholar
Constantin, P., Kukavica, I. & Vicol, V. 2015 Contrast between Lagrangian and Eulerian analytic regularity properties of Euler equations. Ann. Inst. Henri Poincaré 33, 1569–1588.CrossRefGoogle Scholar
Constantin, P., Vicol, V. & Wu, J. 2015 Analyticity of Lagrangian trajectories for well-posed inviscid incompressible fluid models. Adv. Maths 285, 352–393.CrossRefGoogle Scholar
Courant, R. & Hilbert, D. 1966 Methods of Mathematical Physics. Interscience.Google Scholar
D’Avignon, E., Morrison, P. & Lingam, M. 2016 Derivation of the Hall and extended magnetohydrodynamics. Phys. Plasmas 23, 062101.Google Scholar
De Rham, G. 1984 Differentiable Manifolds. Springer.Google Scholar
Dragt, A. J. & Finn, J. M. 1976 Lie series and invariant functions for analytic symplectic maps. J. Math. Phys. 17, 2215–2227.Google Scholar
Duistermaat, J. J. & Kolk, J. A. C. 2000 Lie Groups. Springer.Google Scholar
Ebin, D. G. & Marsden, J. E. 1970 Groups of diffeomorphisms and the motion of an incompressible fluid. Ann. Maths 92, 102–163.CrossRefGoogle Scholar
Eckart, C. 1960 Variation principles of hydrodynamics. Phys. Fluids 3, 421–427.Google Scholar
Ehlers, J. & Buchert, T. 1997 Newtonian cosmology in Lagrangian formulation: foundations and perturbation theory. Gen. Relativ. Gravit. 29, 733–764.CrossRefGoogle Scholar
Elsasser, W. M. 1956 Hydromagnetic dynamo theory. Rev. Mod. Phys. 28, 135–163.CrossRefGoogle Scholar
Falkovich, G. & Gawedzki, K. 2014 Turbulence on hyperbolic plane: the fate of inverse cascade. J. Stat. Phys. 156, 10–54.Google Scholar
Fecko, M. 2006 Differential Geometry and Lie Groups for Physicists. Cambridge University Press.Google Scholar
Flanders, H. 1963 Differential Forms with Applications to the Physical Sciences. Dover.Google Scholar
Frankel, T. 2012 The Geometry of Physics. Cambridge University Press.Google Scholar
Frisch, U. & Villone, B. 2014 Cauchy’s almost forgotten Lagrangian formulation of the Euler equation for 3D incompressible flow. Eur. Phys. J. H 39, 325–351.Google Scholar
Frisch, U. & Zheligovsky, V. 2014 A very smooth ride in rough sea. Commun. Math. Phys. 326, 499–505.CrossRefGoogle Scholar
Gama, S. & Frisch, U. 1993 Local helicity, a material invariant for the odd-dimensional incompressible Euler equations. In Theory of Solar And Planetary Dynamos (ed. Proctor, M. R. E., Matthews, P. C. & Rucklidge, A. M.), pp. 115–119. Cambridge University Press.Google Scholar
Giaquinta, M. & Hildebrandt, S. 2004 Calculus of Variations. Springer.Google Scholar
Gilbert, A. D. & Vanneste, J.2016 Geometric generalised Lagrangian mean theories. arXiv:1612.07111 [physics.flu-dyn].Google Scholar
Goedbloed, J. P. H. & Poedts, S. 2004 Principles of Magnetohydrodynamics. Cambridge University Press.Google Scholar
Goldstein, H., Poole, C. P. & Safko, J. L. 2001 Classical Mechanics. Addison Wesley.Google Scholar
Gyunter, N. M. [Günther] 1926 Über ein Hauptproblem der Hydrodynamik [On a main problem of hydrodynamics]. Math. Z. 24, 448–499.Google Scholar
Gyunter, N. M. [Gunther] 1934 La théorie du potentiel et ses applications aux problèmes fondamentaux de la physique mathématique. Gauthier–Villars; (English translation: Gyunter, N. M. [Günter], Potential Theory, and its Applications to Basic Problems of Mathematical Physics, Frederick Ungar Publ., NY, 1967).Google Scholar
Hankel, H. 1861 Zur allgemeinen Theorie der Bewegung der Flüssigkeiten. Eine von der philosophishen Facultät der Georgia Augusta am 4. Juni 1861 gekrönte Preisschrift, Göttingen. Dieterichschen Univ.-Buchdruckerei (W. Fr. Kaestner).Google Scholar
Helgason, S. 1962 Differential Geometry and Symmetric Spaces. Academic.Google Scholar
von Helmholtz, H. 1858 Über Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen. J. Reine Angew. Math. 55, 25–55; Translated into English by P. G. Tait, 1867 On Integrals of the Hydrodynamical Equations, which express vortex motion. The London, Edinburgh, and Dublin Philosophical Magazine, Supplement to vol. XXXIII, 485–512.Google Scholar
Hill, H. L. 1951 Hamilton’s principle and the conservation theorem of mathematical physics. Rev. Mod. Phys. 23, 253–260.Google Scholar
Holm, D. D., Schmah, T. & Stoica, C. 2009 Geometric Mechanics and Symmetry. Oxford University Press.Google Scholar
Ibragimov, N. H. 1992 Group analysis of ordinary differential equations and the invariance principle in mathematical physics. Russ. Math. Surv. 47, 89–156.CrossRefGoogle Scholar
Ibragimov, N. H. 1994 CRC Handbook of Lie Group Analysis of Differential Equations, vol. 1–3. CRC.Google Scholar
Ibragimov, N. H. 2013 Transformation Group and Lie Algebras. Higher Education Press.Google Scholar
Ivancevic, V. G. & Ivancevic, T. T. 2007 Applied Differential Geometry. World Scientific.Google Scholar
Jose, J. V. & Saletan, E. J. 1998 Classical Dynamics: A Contemporary Approach. Cambridge University Press.Google Scholar
Khesin, B. A. & Chekanov, Y. V. 1989 Invariants of the Euler equations for ideal or barotropic hydrodynamics and superconductivity in D dimensions. Physica D 40, 119–131.Google Scholar
Khesin, B. A. & Misiolek, G. 2012 The Euler and Navier–Stokes equations on the hyperbolic plane. Proc. Natl Acad. Sci. USA 109, 845–894.CrossRefGoogle ScholarPubMed
Kobayashi, S. & Nomizu, K. 1963 Foundations of Differential Geometry, vol. I. Interscience; 1969, Foundations of Differential Geometry, vol. II. Interscience.Google Scholar
Kuvshinov, B. N. & Schep, T. J. 1997 Geometrical approach to fluids models. Phys. Plasmas 4, 537–550.Google Scholar
Kuzmin, G. A. 1983 Ideal incompressible hydrodynamics in terms of the vortex momentum density. Phys. Lett. A 96, 433–468.Google Scholar
Lagrange, J.-L. 1788 Traité de méchanique analitique. La Veuve Desaint.Google Scholar
Lanczos, C. 1970 The Variational Principles of Mechanics. Dover.Google Scholar
Larsson, J. 1996 A new Hamiltonian formulation for fluids and plasmas. Part 1. The perfect fluid. J. Plasma Phys. 55, 235–259.CrossRefGoogle Scholar
Lax, P. D. 1971 Approximation of measure-preserving transformations. Commun. Pure Appl. Maths 24, 133–135.CrossRefGoogle Scholar
Lichtenstein, L. 1925 Über einige Hilfssätze der Potentialtheorie. I. Math. Z. 23, 72–88.Google Scholar
Lichtenstein, L. 1927 Über einige Existenzprobleme der Hydrodynamik. Math. Z. 26, 196–323.Google Scholar
Lingam, M., Milosevich, G. & Morrison, P. 2016 Concomitant Hamiltonian and topological structures of extended magnetohydrodynamics. Phys. Lett. A 380, 2400–2406.Google Scholar
Liu, X. & Ricca, R. L. 2015 On the derivation of the HOMFLYPT polynomial invariant for fluid knots. J. Fluid Mech. 773, 34–48.Google Scholar
Lovelock, D. & Rund, H. 1989 Tensors, Differential Forms and Variational Principles. Dover.Google Scholar
Luo, G. & Hou, T. Y. 2014 Potentially singular solutions of the 3D axisymmetric Euler equations. Proc. Natl Acad. Sci. USA 111, 12968–12973.Google Scholar
Luo, G. & Hou, T. Y. 2014 Toward the finite-time blowup of the 3D axisymmetric Euler equations: a numerical investigation. Multiscale Model. Simul. 12, 1722–1776.Google Scholar
Marsch, E. & Mangeney, A. 1987 Ideal MHD equations in terms of compressive Elsässer variables. J. Geophys. Res. 92, 7363–7367.Google Scholar
Marsden, J. E. & Ratiu, T. S. 1999 Introduction to Mechanics and Symmetry. Springer.Google Scholar
Moffatt, H. K. 1969 The degree of knotedness of tangled vortex lines. J. Fluid Mech. 35, 117–129.Google Scholar
Moreau, J. J. 1961 Constantes d’un îlot tourbillonnaire en fluide parfait barotrope. C. R. Acad. Sci. Paris 52, 2810–2812.Google Scholar
Nayfeh, A. H. 1998 Perturbation Methods. Wiley Interscience.Google Scholar
Olver, P. J. 1993 Applications of Lie Groups to Differential Equations. Springer.Google Scholar
Oseledets, V. I. 1988 On a new way of writing the Navier–Stokes equation. The Hamiltonian formalism. Commun. Moscow Math. Soc.; Russ. Math. Surveys 44, 1989, 210–211.Google Scholar
Padhye, G. & Morrison, P. J. 1996 Relabeling symmetries in hydrodynamics and magnetohydrodynamics. Plasma Phys. Rep. 22, 869–877.Google Scholar
Podvigina, O., Zheligovsky, V. & Frisch, U. 2016 The Cauchy–Lagrangian method for numerical analysis of Euler flow. J. Comput. Phys. 306, 320–342.Google Scholar
Rampf, C., Villone, B. & Frisch, U. 2015 How smooth are particle trajectories in a 𝛬CDM universe? Mon. Not. R. Astron. Soc. 452, 1421–1436.Google Scholar
Ricca, R. L. & Nipoti, B. 2011 Gauss’ linking number revisited. J. Knot. Theor. Ramif. 20, 1325–1343.CrossRefGoogle Scholar
Sadourny, R., Arakawa, A. & Mintz, Y. 1968 Integration of the nondivergent barotropic vorticity equation with an icosahedral-hexagonal grid for the sphere. Mon. Weath. Rev. 96, 351–356.Google Scholar
Salmon, R. 1988 Hamiltonian fluid mechanics. Annu. Rev. Fluid Mech. 20, 225–256.CrossRefGoogle Scholar
Schutz, B. 1980 Geometrical Methods of Mathematical Physics. Cambridge University Press.Google Scholar
Schwarz, G. 1995 Hodge decomposition – a method for solving boundary value problem. In Lecture Notes in Mathematics, vol. 1607. Springer.Google Scholar
Seifert, U. 1991 Vesicles of toroidal topology. Phys. Rev. Lett. 18, 2404–2407.CrossRefGoogle Scholar
Serre, D. 1984 Invariants et dégénérescence symplectique de l’équation d’Euler des fluides parfaits incompressibles. C. R. Acad. Sci. Paris I 298, 349–352.Google Scholar
Shnirelman, A. 1985 On the geometry of the group of diffeomorphisms and the dynamics of an ideal incompressible fluid. Math. Sbornik. 128, 82–109; Translation from Russian published in 1987 in Mathematics of the USSR-Sbornik 56, 79–105.Google Scholar
Spivak, M. 1979 A Comprehensive Introduction to Differential Geometry. (5 volumes). Publish or Perish.Google Scholar
Steinberg, S. 1986 Lie series, Lie transformations, and their applications. Lect. Notes Phys. 250, 45–103.Google Scholar
Stenberg, S. 1964 Lectures on Differential Geometry. Prentice-Hall.Google Scholar
Tao, T.2016 Finite time blowup for Lagrangian modifications of the three-dimensional Euler equation. arXiv:1606.08481 [math.AP].Google Scholar
Taylor, M. E. 1996 Partial Differential Equations. Part I, II and III. Springer.Google Scholar
Thomson, W. (Lord Kelvin) 1869 VI. – on vortex motion. Trans. R. Soc. Edinburgh 25, 217–260.Google Scholar
Weber, H. 1868 Ueber eine Transformation der hydrodynamischen Gleichungen. J. Reine Angew. Math. 68, 286–292.Google Scholar
Weinberg, S. 1972 Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. Wiley.Google Scholar
Woltjer, L. 1958 A theorem on force-free magnetic fields. Proc. Natl Acad. Sci. USA 44, 489–491.Google Scholar
Zakharov, V. E. & Kuznetsov, E. A. 1997 Hamiltonian formalism for nonlinear waves. Phys.-Usp. 40, 1087–1116; Translated from Usp. Fiz. Nauk 167, 1137–1167, 1997 (in Russian).Google Scholar
Zheligovsky, V. & Frisch, U. 2014 Time-analyticity of Lagrangian particle trajectories in ideal fluid flow. J. Fluid Mech. 749, 404–430.Google Scholar