Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-29T03:17:51.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Generating controllable velocity fluctuations using twin oscillating hydrofoils

Published online by Cambridge University Press:  16 October 2012

S. F. Harding  and
I. G. Bryden
S. F. Harding*
Affiliation:
Institute for Energy Systems, University of Edinburgh, Mayfield Road, Edinburgh EH9 3JL, UK
I. G. Bryden
Affiliation:
Institute for Energy Systems, University of Edinburgh, Mayfield Road, Edinburgh EH9 3JL, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An experiment apparatus has been previously developed with the ability to independently control the instantaneous flow velocity in a water flume. This configuration, which uses two pitching hydrofoils to generate the flow fluctuations, allows the unsteady response of submerged structures to be studied over a wide range of driving frequencies and conditions. Linear unsteady lift theory has been used to calculate the instantaneous circulation about two pitching hydrofoils in uniform flow. A vortex model is then used to describe the circulation in the wakes that determine the velocity perturbations at the centreline between the foils. This paper introduces how the vortex model can be discretized to allow the inverse problem to be solved, such that the foil motions required to recreate a desired velocity time series can be determined. The results of this model are presented for the simplified cases of oscillatory velocity fluctuations in the vertical and stream-wise directions separately, and also simultaneously. The more general case of two-dimensional aperiodic velocity fluctuations is also presented, which demonstrates the capability of configuration between the suggested frequency limits of 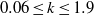$0. 06\leq k\leq 1. 9$.

JFM classification

Vortex Flows: Vortex Flows Wakes/Jets: Vortex streets Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 150 - 158
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashley, H. & Landahl, M. 1956 Aerodynamics of Wings and Bodies. Dover.Google Scholar
Bisplinghoff, R. L., Ashley, H. & Halfman, R. L. 1996 Aeroelasticity. Dover.Google Scholar
Delpero, P. M. 1992 Investigation of flows around a two-dimensional hydrofoil subject to a high reduced frequency gust loading. Master’s thesis, Massachusetts Institute of Technology.Google Scholar
Garrick, I. E. 1938 On some reciprocal relations in the theory of nonstationary flows. Tech. Rep. 629. NACA Technical Report.Google Scholar
Ham, N. D., Bauer, P. H. & Lawrence, T. L. 1974 Wind tunnel generation of sinusoidal lateral and longitudinal gusts by circulation control of twin parallel airfoils. Tech. Rep. 137547. NASA Contractor Report.Google Scholar
Horwich, E. A. 1993 Unsteady response of a two-dimensional hydrofoil subject to high reduced frequency gust loading. Master’s thesis, Massachusetts Institute of Technology.Google Scholar
Jancauskas, E. D. & Melbourne, W. H. 1980 The measurement of aerodynamic admittance using discrete frequency gust generation. In 7th Australasian Hydraulics and Fluid Mechanics Conference. Brisbane. Institution of Engineers.Google Scholar
Jones, R. T. 1940 The unsteady lift of a wing of finite aspect ratio. Tech. Rep. 681. NACA Technical Report.Google Scholar
Leishman, J. G. 2006 Principles of Helicopter Aerodynamics, 2nd edn. Cambridge University Press.Google Scholar
Liepmann, N. W. 1952 On the application of statistical concepts to the buffeting problem. J. Aeronaut. Sci. 19, 793–800.Google Scholar
Passmore, M. A., Richardson, S. & Imam, A. 2001 An experimental study of unsteady vehicle aerodynamics. Proc. Inst. Mech. Engrs Part D: J. Automobile Engineering 215, 779–788.Google Scholar
Penrose, R. 1956 On best approximate solutions of linear matrix equations. Math. Proc. Cambridge Philos. Soc. 52 (1), 17–19.Google Scholar
Poling, D. R. & Telionis, D. P. 1986 The response of airfoils to periodic disturbances – the unsteady Kutta condition. AIAA J. 24 (2), 193–199.CrossRefGoogle Scholar
Sears, W. R. 1941 Some aspects of non-stationary airfoil theory and its practical application. J. Aeronaut. Sci. 8, 104–108.Google Scholar
Stapountzis, H. 1982 An oscillating rig for the generation of sinusoidal flows. J. Phys. E: Sci. Instrum. 15, 1173–1176.CrossRefGoogle Scholar
Tang, D. M., Cizmas, P. G. A. & Dowell, E. H. 1996 Experiments and analysis for a gust generator in a wind tunnel. J. Aircraft 33 (1), 139–148.Google Scholar
Theodorsen, T. 1935 General theory of aerodynamic instability and the mechanism of flutter. Tech. Rep. 496. NACA Technical Report.Google Scholar
Tukey, J. W. 1967 An introduction to the calculations of numerical spectrum analysis. In Spectral Analysis of Time Series (ed. Harris, B.). Wiley.Google Scholar