Article contents
Generalised higher-order Kolmogorov scales
Published online by Cambridge University Press: 30 March 2016
Abstract
Kolmogorov introduced dissipative scales based on the mean dissipation 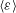 $\langle {\it\varepsilon}\rangle$ and the viscosity
$\langle {\it\varepsilon}\rangle$ and the viscosity  ${\it\nu}$, namely the Kolmogorov length
${\it\nu}$, namely the Kolmogorov length 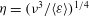 ${\it\eta}=({\it\nu}^{3}/\langle {\it\varepsilon}\rangle )^{1/4}$ and the velocity
${\it\eta}=({\it\nu}^{3}/\langle {\it\varepsilon}\rangle )^{1/4}$ and the velocity 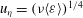 $u_{{\it\eta}}=({\it\nu}\langle {\it\varepsilon}\rangle )^{1/4}$. However, the existence of smaller scales has been discussed in the literature based on phenomenological intermittency models. Here, we introduce exact dissipative scales for the even-order longitudinal structure functions. The derivation is based on exact relations between even-order moments of the longitudinal velocity gradient
$u_{{\it\eta}}=({\it\nu}\langle {\it\varepsilon}\rangle )^{1/4}$. However, the existence of smaller scales has been discussed in the literature based on phenomenological intermittency models. Here, we introduce exact dissipative scales for the even-order longitudinal structure functions. The derivation is based on exact relations between even-order moments of the longitudinal velocity gradient 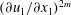 $(\partial u_{1}/\partial x_{1})^{2m}$ and the dissipation
$(\partial u_{1}/\partial x_{1})^{2m}$ and the dissipation 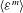 $\langle {\it\varepsilon}^{m}\rangle$. We then find a new length scale
$\langle {\it\varepsilon}^{m}\rangle$. We then find a new length scale 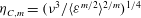 ${\it\eta}_{C,m}=({\it\nu}^{3}/\langle {\it\varepsilon}^{m/2}\rangle ^{2/m})^{1/4}$ and
${\it\eta}_{C,m}=({\it\nu}^{3}/\langle {\it\varepsilon}^{m/2}\rangle ^{2/m})^{1/4}$ and 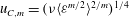 $u_{C,m}=({\it\nu}\langle {\it\varepsilon}^{m/2}\rangle ^{2/m})^{1/4}$, i.e. the dissipative scales depend rather on the moments of the dissipation
$u_{C,m}=({\it\nu}\langle {\it\varepsilon}^{m/2}\rangle ^{2/m})^{1/4}$, i.e. the dissipative scales depend rather on the moments of the dissipation 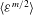 $\langle {\it\varepsilon}^{m/2}\rangle$ and thus the full probability density function (p.d.f.)
$\langle {\it\varepsilon}^{m/2}\rangle$ and thus the full probability density function (p.d.f.) 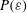 $P({\it\varepsilon})$ instead of powers of the mean
$P({\it\varepsilon})$ instead of powers of the mean 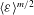 $\langle {\it\varepsilon}\rangle ^{m/2}$. The results presented here are exact for longitudinal even-ordered structure functions under the assumptions of (local) isotropy, (local) homogeneity and incompressibility, and we find them to hold empirically also for the mixed and transverse as well as odd orders. We use direct numerical simulations (DNS) with Reynolds numbers from
$\langle {\it\varepsilon}\rangle ^{m/2}$. The results presented here are exact for longitudinal even-ordered structure functions under the assumptions of (local) isotropy, (local) homogeneity and incompressibility, and we find them to hold empirically also for the mixed and transverse as well as odd orders. We use direct numerical simulations (DNS) with Reynolds numbers from 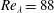 $Re_{{\it\lambda}}=88$ up to
$Re_{{\it\lambda}}=88$ up to 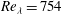 $Re_{{\it\lambda}}=754$ to compare the different scalings. We find that indeed
$Re_{{\it\lambda}}=754$ to compare the different scalings. We find that indeed 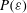 $P({\it\varepsilon})$ or, more precisely, the scaling of
$P({\it\varepsilon})$ or, more precisely, the scaling of 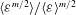 $\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$ as a function of the Reynolds number is a key parameter, as it determines the ratio
$\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$ as a function of the Reynolds number is a key parameter, as it determines the ratio 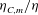 ${\it\eta}_{C,m}/{\it\eta}$ as well as the scaling of the moments of the velocity gradient p.d.f. As
${\it\eta}_{C,m}/{\it\eta}$ as well as the scaling of the moments of the velocity gradient p.d.f. As 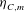 ${\it\eta}_{C,m}$ is smaller than
${\it\eta}_{C,m}$ is smaller than 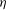 ${\it\eta}$, this leads to a modification of the estimate of grid points required for DNS.
${\it\eta}$, this leads to a modification of the estimate of grid points required for DNS.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 8
- Cited by



