Published online by Cambridge University Press: 08 March 2017
A general constitutive model is constructed and validated for highly concentrated monodisperse emulsions of deformable drops with insoluble surfactant through long-time, large-scale and high-resolution multidrop simulations. There is the same amount of surfactant on each drop, and the linear model is assumed for the surface tension versus the surfactant concentration. The surfactant surface transport is coupled to multidrop hydrodynamics through the convective–diffusive equation and the interfacial stress balance. Only the limit of small surfactant diffusivities is addressed, when this parameter does not affect the rheology. An Oldroyd constitutive equation is postulated, with five variable coefficients depending on one instantaneous flow invariant (chosen as the drop-phase contribution to the dissipation rate). These coefficients are found by fitting the model to five precise rheological functions from two steady base flows at arbitrary deformation rates. One base flow is planar extension (PE) (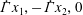 $\dot{\unicode[STIX]{x1D6E4}}x_{1},-\dot{\unicode[STIX]{x1D6E4}}x_{2},0$), the other one is planar mixed flow (PM) (
$\dot{\unicode[STIX]{x1D6E4}}x_{1},-\dot{\unicode[STIX]{x1D6E4}}x_{2},0$), the other one is planar mixed flow (PM) (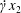 $\dot{\unicode[STIX]{x1D6FE}}x_{2}$,
$\dot{\unicode[STIX]{x1D6FE}}x_{2}$, 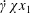 $\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D712}x_{1}$, 0) with
$\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D712}x_{1}$, 0) with 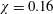 $\unicode[STIX]{x1D712}=0.16$. A small but finite
$\unicode[STIX]{x1D712}=0.16$. A small but finite  $\unicode[STIX]{x1D712}$ (a precise choice in the range
$\unicode[STIX]{x1D712}$ (a precise choice in the range 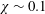 $\unicode[STIX]{x1D712}\sim 0.1$ is unimportant) provides a necessarily perturbation to exclude severe ergodic difficulties and abnormal, kinked behaviour inherent in simple shear for high drop volume fractions
$\unicode[STIX]{x1D712}\sim 0.1$ is unimportant) provides a necessarily perturbation to exclude severe ergodic difficulties and abnormal, kinked behaviour inherent in simple shear for high drop volume fractions  $c$, especially at small capillary numbers
$c$, especially at small capillary numbers 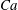 $Ca$ and small drop-to-medium viscosity ratios
$Ca$ and small drop-to-medium viscosity ratios 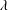 $\unicode[STIX]{x1D706}$. The database rheological functions are obtained for
$\unicode[STIX]{x1D706}$. The database rheological functions are obtained for 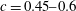 $c=0.45{-}0.6$,
$c=0.45{-}0.6$, 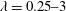 $\unicode[STIX]{x1D706}=0.25{-}3$ and surfactant elasticities
$\unicode[STIX]{x1D706}=0.25{-}3$ and surfactant elasticities 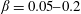 $\unicode[STIX]{x1D6FD}=0.05{-}0.2$ (based on the equilibrium surfactant concentration) from long-time simulations by a multipole-accelerated boundary-integral code with
$\unicode[STIX]{x1D6FD}=0.05{-}0.2$ (based on the equilibrium surfactant concentration) from long-time simulations by a multipole-accelerated boundary-integral code with 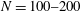 $N=100{-}200$ drops in a periodic cell and 2000–4000 boundary elements per drop. The code is an extension from Zinchenko & Davis (J. Fluid Mech., vol. 779, 2015, pp. 197–244) to account for surfactant transport and Marangoni stresses. Massive drop cusping or (sometimes) drop break-up limit the range of
$N=100{-}200$ drops in a periodic cell and 2000–4000 boundary elements per drop. The code is an extension from Zinchenko & Davis (J. Fluid Mech., vol. 779, 2015, pp. 197–244) to account for surfactant transport and Marangoni stresses. Massive drop cusping or (sometimes) drop break-up limit the range of 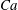 $Ca$ from above in the base flows, but there is no substantial lower limitation owing to the absence of phase transition difficulties. At small
$Ca$ from above in the base flows, but there is no substantial lower limitation owing to the absence of phase transition difficulties. At small 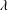 $\unicode[STIX]{x1D706}$, even minimal surface contamination may have a strong effect on the rheology. The simulations remain accurate for quite strong drop interactions, when the PE emulsion viscosity is nine times that for the carrier fluid. The model validation against a steady PM flow with a different
$\unicode[STIX]{x1D706}$, even minimal surface contamination may have a strong effect on the rheology. The simulations remain accurate for quite strong drop interactions, when the PE emulsion viscosity is nine times that for the carrier fluid. The model validation against a steady PM flow with a different 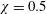 $\unicode[STIX]{x1D712}=0.5$ shows a very good agreement for various
$\unicode[STIX]{x1D712}=0.5$ shows a very good agreement for various 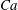 $Ca$,
$Ca$,  $c$ and
$c$ and 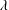 $\unicode[STIX]{x1D706}$. In the three PE and PM time-dependent flow tests, the quasi-steady approximation is found to predict stresses poorly. In contrast, the combination of the steady-state results for PE and PM used in the present method to generate the Oldroyd parameters gives a model with much better predictions for these time-dependent flows.
$\unicode[STIX]{x1D706}$. In the three PE and PM time-dependent flow tests, the quasi-steady approximation is found to predict stresses poorly. In contrast, the combination of the steady-state results for PE and PM used in the present method to generate the Oldroyd parameters gives a model with much better predictions for these time-dependent flows.