Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-16T15:04:16.620Z Has data issue: false hasContentIssue false
  • English
  • Français

A general definition of formation time for starting jets and forced plumes at low Richardson number

Published online by Cambridge University Press:  08 January 2020

Lei Gao Open the ORCID record for Lei Gao [Opens in a new window] ,
Hui-Fen Guo  and
Simon C. M. Yu Open the ORCID record for Simon C. M. Yu [Opens in a new window]
Lei Gao
Affiliation:
School of Aeronautics and Astronautics, Sichuan University, Chengdu, 610065, China
Hui-Fen Guo*
Affiliation:
Interdisciplinary Division of Aeronautical and Aviation Engineering, The Hong Kong Polytechnic University, Kowloon, Hong Kong, China
Simon C. M. Yu
Affiliation:
Interdisciplinary Division of Aeronautical and Aviation Engineering, The Hong Kong Polytechnic University, Kowloon, Hong Kong, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

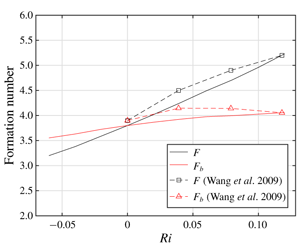
As an important dimensionless parameter for the vortex formation process, the general form of the formation time defined by Dabiri (Annu. Rev. Fluid Mech., vol. 41, 2009, pp. 17–33) is refined so as to provide better normalization for various vortex generator configurations. Our proposed definition utilizes the total circulation over the entire flow domain rather than that of the forming vortex ring alone. It adopts an integral form by considering the instantaneous infinitesimal increment in the formation time so that the effect of temporally varying properties of the flow configuration can be accounted for properly. By including the effect of buoyancy, the specific form of the general formation time for the starting forced plumes with negative and positive buoyancy is derived. A theoretical prediction based on the Kelvin–Benjamin variational principle shows that the general formation time manifests the invariance of the critical time scale, i.e. the formation number, under the influence of a source–ambient density difference. It demonstrates that the general formation time, based on the circulation production over the entire flow field, could take into account the effect of various vorticity production mechanisms, such as from a flux term or in a baroclinic fluid, on the critical formation number. The proposed definition may, therefore, serve as a guideline for deriving the specific form of the formation time in other types of starting/pulsatile flows.

JFM classification

Vortex Flows: Vortex dynamics Wakes/Jets: Jets Geophysical and Geological Flows: Baroclinic flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 886 , 10 March 2020 , A6
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ai, J. J., Law, A. W. K. & Yu, S. C. M. 2006 On Boussinesq and non-Boussinesq starting forced plumes. J. Fluid Mech. 558, 357–386.CrossRefGoogle Scholar
Dabiri, J. O. 2009 Optimal vortex formation as a unifying principle in biological propulsion. Annu. Rev. Fluid Mech. 41, 17–33.CrossRefGoogle Scholar
Dabiri, J. O. & Gharib, M. 2005 Starting flow through nozzles with temporally variable exit diameter. J. Fluid Mech. 538, 111–136.CrossRefGoogle Scholar
Didden, N. 1979 On the formation of vortex rings: rolling-up and production of circulation. Z. Angew. Math. Phys. 30 (1), 101–116.CrossRefGoogle Scholar
Gao, L. & Yu, S. C. M. 2016 Vortex ring formation in starting forced plumes with negative and positive buoyancy. Phys. Fluids 28 (11), 113601.CrossRefGoogle Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Hurridge, H. & Hunt, G. 2012 The rise heights of low- and high-Froude-number turbulent axisymmetric fountains. J. Fluid Mech. 691, 392–416.CrossRefGoogle Scholar
Iglesias, I., Vera, M., Sánchez, A. L. & Liñán, A. 2005 Simulations of starting gas jets at low Mach numbers. Phys. Fluids 17 (3), 038105.CrossRefGoogle Scholar
Jeon, D. & Gharib, M. 2004 On the relationship between the vortex formation process and cylinder wake vortex patterns. J. Fluid Mech. 519, 161–181.CrossRefGoogle Scholar
Lundgren, T. S., Yao, J. & Mansour, N. N. 1992 Microburst modelling and scaling. J. Fluid Mech. 239, 461–488.CrossRefGoogle Scholar
Marugán-Cruz, C., Rodríguez-Rodríguez, J. & Martínez-Bazán, C. 2009 Negatively buoyant starting jets. Phys. Fluids 21 (11), 117101.CrossRefGoogle Scholar
Marugán-Cruz, C., Rodríguez-Rodríguez, J. & Martínez-Bazán, C. 2013 Formation regimes of vortex rings in negatively buoyant starting jets. J. Fluid Mech. 716, 470–486.CrossRefGoogle Scholar
Milano, M. & Gharib, M. 2005 Uncovering the physics of flapping flat plates with artificial evolution. J. Fluid Mech. 534, 403–409.CrossRefGoogle Scholar
Mohseni, K. & Gharib, M. 1998 A model for universal time scale of vortex ring formation. Phys. Fluids 10, 2436–2438.CrossRefGoogle Scholar
Pantzlaff, L. & Lueptow, R. M. 1999 Transient positively and negatively buoyant turbulent round jets. Exp. Fluids 27, 117–125.CrossRefGoogle Scholar
Pottebaum, T. S. & Gharib, M. 2004 The pinch-off process in a starting buoyant plume. Exp. Fluids 37 (1), 87–94.CrossRefGoogle Scholar
Ringuette, M. J., Milano, M. & Gharib, M. 2007 Role of the tip vortex in the force generation of low-aspect-ratio normal flat plates. J. Fluid Mech. 581, 453–468.CrossRefGoogle Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24 (1), 235–279.CrossRefGoogle Scholar
Shusser, M. & Gharib, M. 2000 A model for vortex ring formation in a starting buoyant plume. J. Fluid Mech. 416, 173–185.CrossRefGoogle Scholar
Wang, R.-Q., Law, A. W. K. & Adams, E. E. 2011 Pinch-off and formation number of negatively buoyant jets. Phys. Fluids 23 (5), 052101.CrossRefGoogle Scholar
Wang, R.-Q., Law, A. W. K., Adams, E. E. & Fringer, O. B. 2009 Buoyant formation number of a starting buoyant jet. Phys. Fluids 21 (12), 125104.CrossRefGoogle Scholar
Zhao, W., Frankel, S. H. & Mongeau, L. G. 2000 Effects of trailing jet instability on vortex ring formation. Phys. Fluids 12, 589–596.CrossRefGoogle Scholar