Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sun, Ming-bo
and
Hu, Zhi-wei
2018.
Mixing in nearwall regions downstream of a sonic jet in a supersonic crossflow at Mach 2.7.
Physics of Fluids,
Vol. 30,
Issue. 10,
Sun, Mingbo
Sandham, Neil D.
and
Hu, Zhiwei
2019.
Turbulence structures and statistics of a supersonic turbulent boundary layer subjected to concave surface curvature.
Journal of Fluid Mechanics,
Vol. 865,
Issue. ,
p.
60.
Sun, Mingbo
Wang, Hongbo
and
Xiao, Feng
2019.
Jet in Supersonic Crossflow.
p.
103.
Du, Zhao-bo
Huang, Wei
and
Yan, Li
2019.
Parametric study on mixing augmentation mechanism induced by air injection in a shock-induced combustion ramjet engine.
Energy,
Vol. 186,
Issue. ,
p.
115895.
Prasad, Chitrarth
and
Morris, Philip
2019.
Effect of fluid injection on turbulence and noise reduction of a supersonic jet.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 377,
Issue. 2159,
p.
20190082.
Sun, Mingbo
Liu, Yuan
and
Hu, Zhiwei
2019.
Turbulence decay in a supersonic boundary layer subjected to a transverse sonic jet.
Journal of Fluid Mechanics,
Vol. 867,
Issue. ,
p.
216.
Huang, Wei
Du, Zhao-bo
Yan, Li
and
Xia, Zhi-xun
2019.
Supersonic mixing in airbreathing propulsion systems for hypersonic flights.
Progress in Aerospace Sciences,
Vol. 109,
Issue. ,
p.
100545.
Prasad, Chitrarth
and
Morris, Philip J.
2019.
Unsteady Simulations of Fluid Inserts for Supersonic Jet Noise Reduction.
Sun, Mingbo
Wang, Hongbo
and
Xiao, Feng
2019.
Jet in Supersonic Crossflow.
p.
55.
Du, Zhao-bo
Huang, Wei
Yan, Li
Li, Lang-quan
Chen, Zheng
and
Li, Shi-bin
2019.
RANS study of steady and pulsed gaseous jets into a supersonic crossflow.
International Journal of Heat and Mass Transfer,
Vol. 136,
Issue. ,
p.
157.
Li, Guang-Xin
Sun, Ming-Bo
Yu, Jiang-Fei
Liang, Chang-Hai
Liu, Yuan
Zhao, Guo-Yan
and
Huang, Yu-Hui
2020.
Effect of Injection Mach Number on Penetration in a Supersonic Crossflow.
AIAA Journal,
Vol. 58,
Issue. 3,
p.
1216.
Rasheed, Imran
and
Mishra, Debi Prasad
2020.
Numerical study of a sonic jet in a supersonic crossflow over a flat plate.
Physics of Fluids,
Vol. 32,
Issue. 12,
Sebastian, Robin
Lürkens, Thomas
and
Schreyer, Anne-Marie
2020.
Flow field around a spanwise-inclined jet in supersonic crossflow.
Aerospace Science and Technology,
Vol. 106,
Issue. ,
p.
106209.
Liang, Chang-hai
Sun, Ming-bo
Liu, Yuan
Li, Guang-xin
and
Yu, Jiang-fei
2020.
Numerical study of flow structures and mixing characteristics of a sonic jet in supersonic crossflow.
Acta Astronautica,
Vol. 166,
Issue. ,
p.
78.
Liang, Chang-hai
Sun, Ming-bo
Wang, Qian-cheng
Liu, Yuan
Yang, Yi-xin
Sun, Yong-chao
and
Li, Guang-xin
2020.
Experimental study of parallel injections with different distances into a supersonic crossflow.
Acta Astronautica,
Vol. 168,
Issue. ,
p.
242.
Qin, Shijie
Sun, Shuai
Yoon, Kyungduck
Fang, Hezhen
Chen, Ying
and
Wu, Dazhuan
2021.
Investigation on the internal flow of ventilated partial cavity.
Physics of Fluids,
Vol. 33,
Issue. 8,
Ma, Guangwei
Sun, Mingbo
Zhao, Guoyan
Liu, Pei
Tang, Tao
Fan, Li
Wang, Hongbo
and
Vahala, Linda L.
2021.
Numerical Investigation of an Axisymmetric Model Scramjet Assisted with Cavity of Different Aft Wall Angles.
International Journal of Aerospace Engineering,
Vol. 2021,
Issue. ,
p.
1.
Bae, Ji-Yeul
Kim, Jihyuk
Lee, Namkyu
Bae, Hyung Mo
and
Cho, Hyung Hee
2021.
Measurement of surface heat transfer caused by interaction of sonic jet and supersonic crossflow near injection hole.
Aerospace Science and Technology,
Vol. 119,
Issue. ,
p.
107180.
Laurence, S. J.
Ozawa, H.
Martinez Schramm, J.
and
Hannemann, K.
2021.
Combined combustion and heat-flux measurements on a supersonic jet-in-crossflow configuration using luminescent paint.
Experiments in Fluids,
Vol. 62,
Issue. 7,
Liang, Changhai
Sun, Mingbo
Huang, Yuhui
Liu, Yuan
Zhao, Guoyan
Yang, Yixin
Zhu, Jiajian
Wang, Hongbo
Li, Fan
and
Ma, Guangwei
2021.
Scale effect of gas injection into a supersonic crossflow.
Aerospace Science and Technology,
Vol. 117,
Issue. ,
p.
106947.
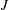 $J$) of 2.3 and 5.5. It is identified that collision shock waves behind the jet induce a herringbone separation bubble in the near-wall jet wake and a reattachment valley is formed and embayed by the herringbone recirculation zone. The recirculating flow in the jet leeward separation bubble forms a primary trailing counter-rotating vortex pair (TCVP) close to the wall surface. Analysis on streamlines passing the separation region shows that the wing of the herringbone separation bubble serves as a micro-ramp vortex generator and streamlines acquire angular momentum downstream to form a secondary surface TCVP in the reattachment valley. Herringbone separation wings disappear in the far field due to the cross-interaction of lateral supersonic flow and the expansion flow in the reattachment valley, which also leads to the vanishing of the secondary TCVP. A three-dimensional schematic of surface trailing wakes is presented and explains the formation mechanisms of the surface TCVPs.
$J$) of 2.3 and 5.5. It is identified that collision shock waves behind the jet induce a herringbone separation bubble in the near-wall jet wake and a reattachment valley is formed and embayed by the herringbone recirculation zone. The recirculating flow in the jet leeward separation bubble forms a primary trailing counter-rotating vortex pair (TCVP) close to the wall surface. Analysis on streamlines passing the separation region shows that the wing of the herringbone separation bubble serves as a micro-ramp vortex generator and streamlines acquire angular momentum downstream to form a secondary surface TCVP in the reattachment valley. Herringbone separation wings disappear in the far field due to the cross-interaction of lateral supersonic flow and the expansion flow in the reattachment valley, which also leads to the vanishing of the secondary TCVP. A three-dimensional schematic of surface trailing wakes is presented and explains the formation mechanisms of the surface TCVPs.