Published online by Cambridge University Press: 03 August 2016
We present a three-region model for the time-averaged behaviour of established turbulent axisymmetric fountains at high source Froude numbers 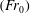 $(Fr_{0})$ in which we uniquely account for entrainment of ambient fluid both laterally and at the fountain top. High-
$(Fr_{0})$ in which we uniquely account for entrainment of ambient fluid both laterally and at the fountain top. High-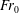 $Fr_{0}$ ‘forced’ fountains, as originally investigated experimentally by Turner (J. Fluid Mech., vol. 26 (4), 1966, pp. 779–792), are characterised by an upflow, a counterflow and a fountain top where the flow reverses direction. Through the inclusion of the flow-reversal region and by accounting for fountain-top entrainment, which is neglected in all existing models, close agreement is achieved between our solutions and existing experimental data. Moreover, our predictions of the fluxes within the fountain are in accord with scaling arguments deduced in recent studies. Our model reveals five key ratios that characterise the fountain asymptote to constant values in the high-
$Fr_{0}$ ‘forced’ fountains, as originally investigated experimentally by Turner (J. Fluid Mech., vol. 26 (4), 1966, pp. 779–792), are characterised by an upflow, a counterflow and a fountain top where the flow reverses direction. Through the inclusion of the flow-reversal region and by accounting for fountain-top entrainment, which is neglected in all existing models, close agreement is achieved between our solutions and existing experimental data. Moreover, our predictions of the fluxes within the fountain are in accord with scaling arguments deduced in recent studies. Our model reveals five key ratios that characterise the fountain asymptote to constant values in the high-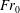 $Fr_{0}$ limit. These are the ratios of the (1) initial and mean rise heights, (2) vertical extents of the fountain top and upflow regions, (3) fluxes of volume entrained into the fountain top and entrained laterally into the counterflow, (4) forces of inertia and buoyancy acting on the counterflow at the level of the source and (5) average times taken for fluid to rise through the upflow and fall through the counterflow. Attributing the invariance of these ratios to the global self-preserving behaviour of the fountain, we propose a threshold source Froude number for which a continuous negatively buoyant release may be regarded as giving rise to a ‘forced’ fountain.
$Fr_{0}$ limit. These are the ratios of the (1) initial and mean rise heights, (2) vertical extents of the fountain top and upflow regions, (3) fluxes of volume entrained into the fountain top and entrained laterally into the counterflow, (4) forces of inertia and buoyancy acting on the counterflow at the level of the source and (5) average times taken for fluid to rise through the upflow and fall through the counterflow. Attributing the invariance of these ratios to the global self-preserving behaviour of the fountain, we propose a threshold source Froude number for which a continuous negatively buoyant release may be regarded as giving rise to a ‘forced’ fountain.