Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-18T00:16:41.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Forced dynamics of a short viscous liquid bridge

Published online by Cambridge University Press:  18 November 2014

L. Vincent ,
L. Duchemin  and
S. Le Dizès
L. Vincent
Affiliation:
Aix-Marseille Université, CNRS, Centrale Marseille, IRPHE UMR 7342, 13384 Marseille, France
L. Duchemin
Affiliation:
Aix-Marseille Université, CNRS, Centrale Marseille, IRPHE UMR 7342, 13384 Marseille, France
S. Le Dizès*
Affiliation:
Aix-Marseille Université, CNRS, Centrale Marseille, IRPHE UMR 7342, 13384 Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of an axisymmetric liquid bridge of a fluid of density 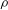${\it\rho}$, viscosity 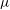${\it\mu}$ and surface tension ${\it\sigma}$ held between two co-axial disks of equal radius $e$ is studied when one disk is slowly moved with a velocity 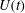$U(t)$. The analysis is performed using a one-dimensional model for thin bridges. We consider attached boundary conditions (the contact line is fixed to the boundary of the disk), neglect gravity and limit our analysis to short bridges such that there exists a stable equilibrium shape. This equilibrium is a Delaunay curve characterized by the two geometric parameters 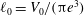$\ell _{0}=V_{0}/({\rm\pi}e^{3})$ and 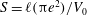$S=\ell ({\rm\pi}e^{2})/V_{0}$, where $V_{0}$ is the volume of fluid and 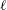$\ell$ the length of the bridge. Our objective is to analyse the departure of the dynamical solution from the static Delaunay shape as a function of 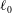$\ell _{0}$, 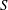$S$, the Ohnesorge number 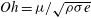$Oh={\it\mu}/\sqrt{{\it\rho}{\it\sigma}e}$, and the instantaneous velocity 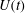$U(t)$ and acceleration 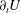$\partial _{t}U$ (non-dimensionalized using $e$ and 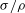${\it\sigma}/{\it\rho}$) of the disk. Using a perturbation theory for small velocity and acceleration, we show that (i) a non-homogeneous velocity field proportional to 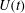$U(t)$ and independent of 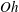$Oh$ is present within the bridge; (ii) the area correction to the equilibrium shape can be written as $U^{2}A_{i}+U\,Oh\,A_{v}+\partial _{t}UA_{a}$ where 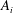$A_{i}$, 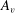$A_{v}$ and 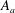$A_{a}$ are functions of 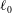$\ell _{0}$ and 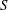$S$ only. The characteristics of the velocity field and the shape corrections are analysed in detail. For the case of a cylinder (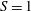$S=1$), explicit expressions are derived and used to provide some insight into the break-up that the deformation would induce. The asymptotic results are validated and tested by direct numerical simulations when the velocity is constant and when it oscillates. For the constant velocity case, we demonstrate that the theory provides a very good estimate of the dynamics for a large range of parameters. However, a systematic departure is observed for very small $Oh$ due to the persistence of free eigenmodes excited during the transient. These same eigenmodes also limit the applicability of the theory to oscillating bridges with large oscillating periods. Finally, the perturbation theory is applied to the cylindrical solution of Frankel & Weihs (J. Fluid Mech., vol. 155 (1985), pp. 289–307) obtained for constant velocity 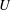$U$ when the contact lines are allowed to move. We show that it can be used to compute the correction associated with acceleration. Finally, the effect of gravity is discussed and shown to modify the equilibrium shape but not the main results obtained from the perturbation theory.

JFM classification

Drops and Bubbles: Breakup/coalescence Interfacial Flows (free surface): Liquid bridges
Type
Papers
Information
Journal of Fluid Mechanics , Volume 761 , 25 December 2014 , pp. 220 - 240
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambravaneswaran, B., Wilkes, E. D. & Basaran, O. A. 2002 Drop formation from a capillary tube: comparison of one-dimensional and two-dimensional analyses and occurrence of satellite drops. Phys. Fluids 14 (8), 2606–2621.Google Scholar
Bhat, P. P., Basaran, O. A. & Pasquali, M. 2008 Dynamics of viscoelastic liquid filaments: Low capillary number flows. J. Non-Newtonian Fluid Mech. 150, 211–225.CrossRefGoogle Scholar
Bogy, D. B. 1978 Use of one-dimensional Cosserat theory to study instability in a viscous liquid jet. Phys. Fluids 21 (2), 190–197.CrossRefGoogle Scholar
Borkar, A. & Tsamopoulos, J. 1991 Boundary-layer analysis of the dynamics of axisymmetric capillary bridges. Phys. Fluids A 3 (12), 2866–2874.Google Scholar
Chen, T.-Y. & Tsamopoulos, J. 1993 Nonlinear dynamics of capillary bridges: theory. J. Fluid Mech. 255, 373–409.CrossRefGoogle Scholar
Cheong, B. S. & Howes, T. 2004 Capillary jet instability under the influence of gravity. Chem. Engng Sci. 59, 2145–2157.Google Scholar
Dodds, S., Carvalho, M. & Kumar, S. 2011 Stretching liquid bridges with moving contact lines: The role of inertia. Phys. Fluids 23, 092101.CrossRefGoogle Scholar
Eggers, J. 1997 Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys. 69 (3), 865–929.Google Scholar
Eggers, J. & Dupont, T. F. 1994 Drop formation in a one-dimensional approximation of the Navier–Stokes equation. J. Fluid Mech. 262, 205–221.CrossRefGoogle Scholar
Eggers, J. & Villermaux, E. 2008 Physics of fluid jets. Rep. Prog. Phys. 71, 1–79.Google Scholar
Fowle, A. A., Wang, C. A. & Strong, P. F. 1979 Experiments on the stability of conical and cylindrical liquid columns at low bond numbers. In Proceedings of the Third European Symposium on Material Science in Space (ESA SP-142), pp. 317–325.Google Scholar
Frankel, I. & Weihs, D. 1985 Stability of a capillary jet with linearly increasing axial velocity (with application to shaped charges). J. Fluid Mech. 155, 289–307.Google Scholar
Gaudet, S., McKinley, G. H. & Stone, H. A. 1996 Extensional deformation of Newtonian liquid bridges. Phys. Fluids 8 (10), 2567–2579.Google Scholar
Gillette, R. D. & Dyson, D. C. 1970 Stability of fluid interfaces of revolution between equal solid circular plates. Chem. Engng J. 2 (1), 44–54.CrossRefGoogle Scholar
Johnson, M., Kamm, R. D., Ho, L. W., Shapiro, A. & Pedley, T. J. 1991 The nonlinear growth of surface-tension-driven instabilities of a thin annular film. J. Fluid Mech. 233, 141–156.Google Scholar
Kroger, R., Berg, S., Delgado, A. & Rath, H. J. 1992 Stretching behavior of large polymeric and Newtonian liquid bridges in plateau simulation. J. Non-Newtonian Fluid Mech. 45 (3), 385–400.Google Scholar
Le Merrer, M., Seiwert, J., Quéré, D. & Clanet, C. 2008 Shapes of hanging viscous filaments. Eur. Phys. Lett. 84, 56004.Google Scholar
Liao, Y.-C., Franses, E. I. & Basaran, O. A. 2006 Deformation and breakup of a stretching liquid bridge covered with an insoluble surfactant monolayer. Phys. Fluids 18, 022101.Google Scholar
Meseguer, J. 1983 The breaking of an axisymmetric slender liquid bridge. J. Fluid Mech. 130, 123–151.Google Scholar
Mollot, D. J., Tsamopoulos, J., Chen, T.-Y. & Ashgriz, N. 1993 Nonlinear dynamics of capillary bridges: experiments. J. Fluid Mech. 255, 411–435.Google Scholar
Orr, F. M., Scriven, L. E. & Rivas, A. P. 1975 Pendular rings between solids: meniscus properties and capillary force. J. Fluid Mech. 67 (4), 723–742.CrossRefGoogle Scholar
Perales, J. M. & Meseguer, J. 1992 Theoretical and experimental study of the vibration of axisymmetric viscous liquid bridges. Phys. Fluids A 4 (6), 1110–1130.Google Scholar
Plateau, J. A. F. 1873 Statique Expérimentale et Théorique des Liquides Soumis aux Seules Forces Moléculaires. Gauthier-Villars.Google Scholar
Ramos, A., Garcia, F. J. & Valverde, J. M. 1999 On the breakup of slender liquid bridges: Experiments and a 1-D numerical analysis. Eur. J. Mech. (B/Fluids) 18, 649–658.Google Scholar
Sauter, U. S. & Buggisch, H. W. 2013 Stability of initially slow viscous jets driven by gravity. J. Fluid Mech. 533, 237–257.Google Scholar
Slobozhanin, L. A. & Perales, J. M. 1993 Stability of liquid bridges between two equal disks in an axial gravity field. Phys. Fluids A 5 (6), 1305–1314.Google Scholar
Stokes, Y. M., Tuck, E. O. & Schwartz, L. W. 2000 Extensional fall of a very viscous fluid drop. Q. J. Mech. Appl. Maths 53 (4), 565–582.Google Scholar
Tomotika, S. 1936 Breaking up of a drop of viscous liquid immersed in another viscous fluid with is extending at a uniform rate. Proc. R. Soc. Lond. A 153 (879), 302–318.Google Scholar
Tsamopoulos, J., Chen, T.-Y. & Borkar, A. 1992 Viscous oscillations of capillary bridges. J. Fluid Mech. 235, 579–609.Google Scholar
Villermaux, E. 2012 The formation of filamentary structures from molten silicates: Pele’s hair, angel hair, and blown clinker. C. R. Mec. 340 (8), 555–564.CrossRefGoogle Scholar
Zhang, X., Padgett, R. S. & Basaran, O. A. 1996 Nonlinear deformation and breakup of stretching liquid bridges. J. Fluid Mech. 329, 207–245.Google Scholar
Zhang, Y. & Alexander, J. I. D. 1990 Sensitivity of liquid bridges subject to axial residual acceleration. Phys. Fluids A 2, 1966–1974.Google Scholar