Article contents
Flows over surface-mounted bluff bodies with different spanwise widths submerged in a deep turbulent boundary layer
Published online by Cambridge University Press: 27 August 2019
Abstract
The spatio-temporal dynamics of separation bubbles induced by surface-mounted bluff bodies with different spanwise widths and submerged in a thick turbulent boundary layer is experimentally investigated. The streamwise extent of the bluff bodies is fixed at 2.36 body heights and the spanwise aspect ratio (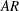 $AR$), defined as the ratio between the width and height, is increased from 1 to 20. The thickness of the upstream turbulent boundary layer is 4.8 body heights, and the dimensionless shear and turbulence intensity evaluated at the body height are 0.23 % and 15.8 %, respectively, while the Reynolds number based on the body height and upstream free-stream velocity is 12 300. For these upstream conditions and limited streamwise extent of the bluff bodies, two distinct and strongly interacting separation bubbles are formed over and behind the bluff bodies. A time-resolved particle image velocimetry is used to simultaneously measure the velocity field within these separation bubbles. Based on the dynamics of the mean separation bubbles over and behind the bluff bodies, the flow fields are categorized into three-dimensional, transitional and two-dimensional regimes. The results indicate that the low-frequency flapping motions of the separation bubble on top of the bluff body with
$AR$), defined as the ratio between the width and height, is increased from 1 to 20. The thickness of the upstream turbulent boundary layer is 4.8 body heights, and the dimensionless shear and turbulence intensity evaluated at the body height are 0.23 % and 15.8 %, respectively, while the Reynolds number based on the body height and upstream free-stream velocity is 12 300. For these upstream conditions and limited streamwise extent of the bluff bodies, two distinct and strongly interacting separation bubbles are formed over and behind the bluff bodies. A time-resolved particle image velocimetry is used to simultaneously measure the velocity field within these separation bubbles. Based on the dynamics of the mean separation bubbles over and behind the bluff bodies, the flow fields are categorized into three-dimensional, transitional and two-dimensional regimes. The results indicate that the low-frequency flapping motions of the separation bubble on top of the bluff body with 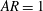 $\mathit{AR}=1$ are primarily influenced by the vortex shedding motion, while those with larger aspect ratios are modulated by the large-scale streamwise elongated structures embedded in the oncoming turbulent boundary layer. For
$\mathit{AR}=1$ are primarily influenced by the vortex shedding motion, while those with larger aspect ratios are modulated by the large-scale streamwise elongated structures embedded in the oncoming turbulent boundary layer. For 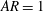 $\mathit{AR}=1$ and 20, the flapping motions in the wake region are strongly influenced by those on top of the bluff bodies but with a time delay that is dependent on the
$\mathit{AR}=1$ and 20, the flapping motions in the wake region are strongly influenced by those on top of the bluff bodies but with a time delay that is dependent on the 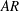 $AR$. Moreover, an expansion of the separation bubble on the top surface tends to lead to an expansion and contraction of separation bubbles in the wake of
$AR$. Moreover, an expansion of the separation bubble on the top surface tends to lead to an expansion and contraction of separation bubbles in the wake of 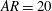 $\mathit{AR}=20$ and 1, respectively. As for the transitional case of
$\mathit{AR}=20$ and 1, respectively. As for the transitional case of 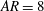 $\mathit{AR}=8$, the separation bubbles over and behind the body are in phase over a wide range of time difference. The dynamics of the shear layer in the wake region of the transitional case is remarkably more complex than the limiting two-dimensional and three-dimensional configurations.
$\mathit{AR}=8$, the separation bubbles over and behind the body are in phase over a wide range of time difference. The dynamics of the shear layer in the wake region of the transitional case is remarkably more complex than the limiting two-dimensional and three-dimensional configurations.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 32
- Cited by


