Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sun, Chenlin
Azmi, Azlin Mohd
Leontini, Justin
Zhu, Hongjun
and
Zhou, Tongming
2021.
Experimental study on the development of wake vortices behind screen cylinders.
Physics of Fluids,
Vol. 33,
Issue. 8,
Dwivedi, Ajay Raj
Dhiman, Amit
and
Sanyal, Aniruddha
2022.
Stratified Shear-Thinning Fluid Flow Past Tandem Cylinders in the Presence of Mixed Convection Heat Transfer With a Channel-Confined Configuration.
Journal of Fluids Engineering,
Vol. 144,
Issue. 5,
Kingora, Kamau
Raza, Mishal Mohammad
and
Sadat, Hamid
2022.
Flow and passive scalar transfer characteristics around a row of interacting tandem cylinders.
Journal of Hydrodynamics,
Vol. 34,
Issue. 4,
p.
596.
Kingora, Kamau
Burks, Wes Lee
and
Sadat, Hamid
2022.
Flow and mass transfer characteristics for interacting side-by-side cylinders.
Physics of Fluids,
Vol. 34,
Issue. 2,
Leontini, Justin S.
and
Sader, John E.
2022.
The dynamics of a rigid inverted flag.
Journal of Fluid Mechanics,
Vol. 948,
Issue. ,
van Hinsberg, Nils Paul
2022.
Two identical tandem square prisms with rounded edges and hard marine fouling at incidence in cross-flow: Effect of spacing and Reynolds number on unsteady fluid dynamics.
Ocean Engineering,
Vol. 262,
Issue. ,
p.
112302.
LIU, Ming-Ming
WANG, Hao-Cheng
SHAO, Fei-Fei
JIN, Xin
Tang, Guo-Qiang
and
YANG, Fan
2022.
Numerical investigation on vortex-induced vibration of an elastically mounted circular cylinder with multiple control rods at low Reynolds number.
Applied Ocean Research,
Vol. 118,
Issue. ,
p.
102987.
Fishman, A.
Rossiter, J. M.
Leontini, J. S.
and
Homer, M. E.
2022.
Mixing in arrays of villi-like actuators.
Physics of Fluids,
Vol. 34,
Issue. 9,
2022.
Eizadi, Hamidreza
An, Hongwei
Zhou, Tongming
Zhu, Hongjun
and
Cheng, Liang
2022.
Wake transitions of six tandem circular cylinders at low Reynolds numbers.
Physics of Fluids,
Vol. 34,
Issue. 2,
Hosseini, N.
Griffith, M.D.
and
Leontini, J.S.
2022.
Flow-induced vibrations in long rows of cylinders and their links to convective instabilities.
International Journal of Heat and Fluid Flow,
Vol. 94,
Issue. ,
p.
108922.
Sun, Xu
Suh, Steve
Ye, Ze-Hua
and
Zhang, Yi-Xin
2022.
Sub-harmonic wake-induced vibration of five tandem circular cylinders at low Reynolds number of 100.
Theoretical and Computational Fluid Dynamics,
Vol. 36,
Issue. 4,
p.
671.
Xu, Xiwang
Yi, Shihe
Quan, Pengcheng
Xiong, Haoxi
and
Nie, Liang
2023.
Experimental study on the hypersonic boundary layer transition induced by tandem cylinders.
Experimental Thermal and Fluid Science,
Vol. 145,
Issue. ,
p.
110901.
Zhang, Luoning
Zhang, Zhimeng
Chen, Weilin
Srinil, Narakorn
Zhu, Hongjun
Bao, Yan
and
Ji, Chunning
2023.
Flow-induced vibrations of ten tandem cylinders at low Reynolds number.
Physics of Fluids,
Vol. 35,
Issue. 12,
Aasland, Tale E.
Pettersen, Bjørnar
Andersson, Helge I.
and
Jiang, Fengjian
2023.
Flow topology in the gap and wake of convex curved tandem cylinders.
Journal of Fluid Mechanics,
Vol. 976,
Issue. ,
Ahmad, Shafee
Shams-ul-Islam
Waqas, Hassan
Liu, Dong
Muhammad, Taseer
Khan, Ilyas
and
Eldin, Sayed M
2023.
Flow transition and fluid forces reduction for flow around two tandem cylinders.
Results in Physics,
Vol. 51,
Issue. ,
p.
106681.
Zhang, Shigang
Han, Yuang
Lacassagne, Tom
Cagney, Neil
Naveira-Cotta, Carolina P.
Balabani, Stavroula
and
Tiwari, Manish K.
2023.
Flow dynamics and mixing past pairs of confined microfluidic cylinders.
Chemical Engineering Science,
Vol. 267,
Issue. ,
p.
118349.
Sharifi Ghazijahani, M.
and
Cierpka, C.
2023.
Flow structure and dynamics behind cylinder arrays at Reynolds number ∼100.
Physics of Fluids,
Vol. 35,
Issue. 6,
Xiao, Jian
and
Jing, Dalei
2024.
Fluid flow and mixing in a channel with dual bluff bodies.
Physics of Fluids,
Vol. 36,
Issue. 1,
Siddiqui, Muhammad Aneeb
Munir, Adnan
Ali, Muhammad Hamza
Zhao, Ming
Duan, Penghao
and
Qadri, Muhammad Nafees Mumtaz
2024.
Numerical study of wake flow across two circular cylinders in tandem arrangement with high rotation speed.
Physics of Fluids,
Vol. 36,
Issue. 12,
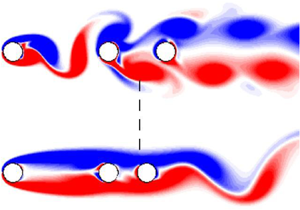
 $Re=200$ have been conducted of the flow past rows of tandem cylinders. It is shown that when the pitch between the two upstream cylinders is large, the wake downstream is characterised by a two-row vortex structure. Placing a third body on the wake centreline in the majority of this two-row structure has basically no impact both upstream and downstream – the third body is cloaked. However, a region is identified where the placement of a body suppresses vortex shedding from the first cylinder and the two-row structure is destroyed, globally broadcasting the presence of the third body. The effect is shown to occur for different third-body shapes. To understand the existence of this broadcasting region, local instability analysis is conducted which shows the majority of the two-row structure to be convectively unstable, with only a small region adjacent to the rear of the second cylinder that is absolutely unstable. This suggests only bodies placed close to the second body will trigger the global change, and this is supported by a global sensitivity analysis and observation from the simulations. However, neither the local analysis nor the global sensitivity analysis explains the presence of a lower limit for the third-body position that will trigger a global change. However the simulation results clearly show that a third body placed very close to the second body does not trigger this change.
$Re=200$ have been conducted of the flow past rows of tandem cylinders. It is shown that when the pitch between the two upstream cylinders is large, the wake downstream is characterised by a two-row vortex structure. Placing a third body on the wake centreline in the majority of this two-row structure has basically no impact both upstream and downstream – the third body is cloaked. However, a region is identified where the placement of a body suppresses vortex shedding from the first cylinder and the two-row structure is destroyed, globally broadcasting the presence of the third body. The effect is shown to occur for different third-body shapes. To understand the existence of this broadcasting region, local instability analysis is conducted which shows the majority of the two-row structure to be convectively unstable, with only a small region adjacent to the rear of the second cylinder that is absolutely unstable. This suggests only bodies placed close to the second body will trigger the global change, and this is supported by a global sensitivity analysis and observation from the simulations. However, neither the local analysis nor the global sensitivity analysis explains the presence of a lower limit for the third-body position that will trigger a global change. However the simulation results clearly show that a third body placed very close to the second body does not trigger this change.


