Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T07:02:57.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Floquet stability analysis of capsules in viscous shear flow

Published online by Cambridge University Press:  13 August 2018

Spencer H. Bryngelson  and
Jonathan B. Freund Open the ORCID record for Jonathan B. Freund [Opens in a new window]
Spencer H. Bryngelson
Affiliation:
Department of Mechanical Science and Engineering, University of Illinois at Urbana–Champaign, Urbana, IL 61801, USA
Jonathan B. Freund*
Affiliation:
Department of Mechanical Science and Engineering, University of Illinois at Urbana–Champaign, Urbana, IL 61801, USA Department of Aerospace Engineering, University of Illinois at Urbana–Champaign, Urbana, IL 61801, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Observations in experiments and simulations show that the kinematic behaviour of an elastic capsule, suspended and rotating in shear flow, depends upon the flow strength, the capsule membrane material properties and its at-rest shape. We develop a linear stability description of the periodically rotating base state of this coupled system, as represented by a boundary integral flow formulation with spherical harmonic basis functions describing the elastic capsule geometry. This yields Floquet multipliers that classify the stability of the capsule motion for elastic capillary numbers 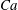$Ca$ ranging from 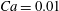$Ca=0.01$ to 5. Viscous dissipation rapidly damps most perturbations. However, for all cases, a single component grows or decays slowly, depending upon 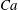$Ca$, over many periods of the rotation. The transitions in this stability behaviour correspond to the different classes of rotating motion observed in previous studies.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Capsule/cell dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 852 , 10 October 2018 , pp. 663 - 677
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, J. C. & Swarztrauber, P. N.1997 SPHEREPACK 2.0: a model development facility. Tech. Rep. NCAR/TN-436-STR. NCAR.Google Scholar
Aouane, O., Thiébaud, M., Benyoussef, A., Wagner, C. & Misbah, C. 2014 Vesicle dynamics in a confined Poiseuille flow: from steady state to chaos. Phys. Rev. E 90 (3), 033011.Google Scholar
Bagheri, S. 2013 Koopman-mode decomposition of the cylinder wake. J. Fluid Mech. 726, 596–623.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Barthès-Biesel, D. 2009 Capsule motion in flow: deformation and membrane buckling. C. R. Phys. 10, 764–774.Google Scholar
Barthès-Biesel, D. 2016 Motion and deformation of elastic capsules and vesicles in flow. Annu. Rev. Fluid Mech. 48, 25–52.Google Scholar
Blackburn, H. M. & Lopez, J. M. 2003 The onset of three-dimensional standing and modulated travelling waves in a periodically driven cavity flow. J. Fluid Mech. 497, 289–317.Google Scholar
Blennerhassett, P. J. & Bassom, A. P. 2002 The linear stability of flat Stokes layers. J. Fluid Mech. 464, 393–410.Google Scholar
Blennerhassett, P. J. & Bassom, A. P. 2007 The linear stability of high-frequency oscillatory flow in a torsionally oscillating cylinder. J. Fluid Mech. 576, 491–505.Google Scholar
Bryngelson, S. H. & Freund, J. B. 2016 Capsule-train stability. Phys. Rev. Fluids 1, 033201.Google Scholar
Bryngelson, S. H. & Freund, J. B. 2018 Global stability of flowing red blood cell trains. Phys. Rev. Fluids 3, 073101.Google Scholar
Cazemier, W., Verstappen, R. W. C. P. & Veldman, A. E. P. 1998 Proper orthogonal decomposition and low-dimensional models for driven cavity flows. Phys. Fluids 10 (7), 1685–1699.Google Scholar
Chang, T. M. 2010 Blood replacement with nanobiotechnologically engineered hemoglobin and hemoglobin nanocapsules. Wiley Intersci. Rev. Nanomed. Nanobiotechnol. 2, 418–430.Google Scholar
Cordasco, D. & Bagchi, P. 2013 Orbital drift of capsules and red blood cells in shear flow. Phys. Fluids 25, 091902.Google Scholar
Davies, C., Thomas, C., Bassom, A. P. & Blennerhassett, P. J. 2015 The linear impulse response of disturbances in an oscillatory Stokes layer. Procedia IUTAM 14, 381–384.Google Scholar
Dey, N. S., Majumdar, S. & Rao, M. E. B. 2008 Multiparticulate drug delivery systems for controlled release. Trop. J. Pharm. Res. 7 (3), 1067–1075.Google Scholar
Dupire, J., Abkarian, M. & Viallat, A. 2010 Chaotic dynamics of red blood cells in a sinusoidal flow. Phys. Rev. Lett. 104, 168101.Google Scholar
Dupont, C., Delahaye, F., Barthès-Biesel, D. & Salsac, A.-V. 2016 Stable equilibrium configurations of an oblate capsule in simple shear flow. J. Fluid Mech. 791, 738–757.Google Scholar
Dupont, C., Salsac, A.-V. & Barthès-Biesel, D. 2013 Off-plane motion of a prolate capsule in shear flow. J. Fluid Mech. 721, 180–198.Google Scholar
Einarsson, J., Angilella, J. R. & Mehlig, B. 2014 Orientational dynamics of weakly inertial axisymmetric particles in steady viscous flow. Physica D 278–279, 79–85.Google Scholar
Foessel, E., Walter, J., Salsac, A.-V. & Barthès-Biesel, D. 2011 Influence of internal viscosity on the large deformation and buckling of a spherical capsule in simple shear flow. J. Fluid Mech. 672, 477–486.Google Scholar
Freund, J. B. & Zhao, H.2010 Hydrodynamics of Capsules and Biological Cells, chap. A. Fast high-resolution boundary integral method for multiple interacting blood cells, pp. 71–111. Chapman and Hall/CRC.Google Scholar
Furlow, B. 2009 Contrast-enhanced ultrasound. Radiol. Technol. 80, 547–561.Google Scholar
Gåserød, O., Sannes, A. & Skjåk-Bræk, G. 1999 Microcapsules of alginate–chitosan. II. A study of capsule stability and permeability. Biomaterials 20 (8), 773–783.Google Scholar
Gibbs, B. F., Kermasha, S., Alli, I. & Mulligan, C. N. 1999 Encapsulation in the food industry: a review. Intl J. Food Sci. Neut. 50, 213–224.Google Scholar
Gioria, R. S., Jabardo, P. J. S., Carmo, B. S. & Meneghini, J. R. 2009 Floquet stability analysis of the flow around an oscillating cylinder. J. Fluids Struct. 25, 676–686.Google Scholar
Goosen, M. F., O’Shea, G. M., Gharapetian, H. M., Chou, S. & Sun, A. M. 1985 Optimization of microencapsulation parameters: semipermeable microcapsules as a bioartifical pancreas. Biotechnol. Bioengng 27 (2), 146–150.Google Scholar
Guckenberger, A. & Gekle, S. 2017 Theory and algorithms to compute Helfrich bending forces: a review. J. Phys.: Condens. Matter 29 (20), 203001.Google Scholar
Juniper, M. 2011 Triggering in the horizontal Rijke tube: non-normality, transient growth and bypass transition. J. Fluid Mech. 667, 272–308.Google Scholar
Kim, S. & Karrila, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann.Google Scholar
Kuhtreiber, W. M., Lanza, R. P. & Chick, W. L. 1998 Cell Encapsulation Technology and Therapeutics. Birkhäuser.Google Scholar
Lac, E., Barthès-Biesel, D., Pelekasis, N. A. & Tsamopoulos, J. 2004 Spherical capsules in three-dimensional unbounded Stokes flows: effect of the membrane constitutive law and onset of buckling. J. Fluid Mech. 516, 303–334.Google Scholar
Leelajariyakul, S., Noguchi, H. & Kiatkamjornwong, S. 2008 Surface-modified and micro-encapsulated pigmented inks for ink jet printing on textile fabrics. Prog. Org. Coat. 62 (2), 145–161.Google Scholar
Lim, F. 1984 Biomedical Applications of Microencapsulations, 1st edn. CRC.Google Scholar
Liu, J. 2003 A First Course in the Qualitative Theory of Differential Equations. Prentice Hall.Google Scholar
Martins, I. M., Barreiro, M. F., Coelho, M. & Rodrigues, A. E. 2014 Microencapsulation of essential oils with biodegradable polymeric carriers for cosmetic applications. Chem. Engng J. 245, 191–200.Google Scholar
Miyazawa, K., Yajima, I., Kaneda, I. & Yanaki, T. 2000 Preparation of a new soft capsule for cosmetics. J. Cosmet. Sci. 51 (4), 239–252.Google Scholar
Paret, N., Trachsel, A., Berthier, D. L. & Herrmann, A. 2015 Controlled release of encapsulated bioactive volatiles by rupture of the capsule wall through the light-induced generation of a gas. Chem. Intl Ed. 54 (7), 2275–2279.Google Scholar
Pier, B. & Schmid, P. J. 2017 Linear and nonlinear dynamics of pulsatile channel flow. J. Fluid Mech. 815, 435–480.Google Scholar
Pop, F. 2011 Chemical stabilization of oils rich in long-chain polyunsaturated fatty acids during storage. Food Sci. Technol. Intl 17 (2), 111–117.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Pumhössel, T., Hehenberger, P. & Zeman, K. 2014 Reduced-order modelling of self-excited, time-periodic systems using the method of proper orthogonal decomposition and the Floquet theory. Math. Comput. Model. Dyn. Syst. 20 (6), 528–545.Google Scholar
Rallison, J. M. & Acrivos, A. 1978 A numerical study of the deformation and burst of a viscous drop in an extensional flow. J. Fluid Mech. 89, 191–200.Google Scholar
Rochal, S. B., Lorman, V. L. & Mennessier, G. 2005 Viscoelastic dynamics of spherical composite vesicles. Phys. Rev. E 71, 021905.Google Scholar
Rowley, C. W., Mezic, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Sacker, R.1964 On invariant surfaces and bifurcation of periodic solutions of ordinary differential equations. Tech. Rep. IMM-NYU 333. New York University.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Schmid, P. J. & Henningson, D. S. 2012 Stability and Transition in Shear Flows. Springer Science and Business Media.Google Scholar
Schmid, P. J. & Kytomaa, H. K. 1994 Transient and asymptotic stability of granular flow. J. Fluid Mech. 264, 255–275.Google Scholar
Sheard, G. J., Fitzgerald, M. J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2003 From spheres to circular cylinders: the stability and flow structures of bluff ring wakes. J. Fluid Mech. 492, 147–180.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004 From spheres to circular cylinders: non-axisymmetric transitions in the flow past rings. J. Fluid Mech. 506, 45–78.Google Scholar
Skalak, R., Tozeren, A., Zarda, P. R. & Chien, S. 1973 Strain energy function of red blood cell membranes. Biophys. J. 13, 245–264.Google Scholar
Skotheim, J. M. & Secomb, T. W. 2007 Red blood cells and other nonspherical capsules in shear flow: oscillatory dynamics and the tank-treading-to-tumbling transition. Phys. Rev. Lett. 98 (7), 078301.Google Scholar
Thomas, C., Bassom, A. P. & Blennerhassett, P. J. 2012 The linear stability of oscillating pipe flow. Phys. Fluids 24, 014106.Google Scholar
Thomas, C., Blennerhassett, P. J., Bassom, A. P. & Davies, C. 2015 The linear stability of a Stokes layer subjected to high-frequency perturbations. J. Fluid Mech. 764, 193–218.Google Scholar
Verhulst, F. 2006 Nonlinear Differential Equations and Dynamical Systems. Springer.Google Scholar
Vericella, J. J., Baker, S. E., Stolaroff, J. K., Duoss, E. B., Hardin, J. O. IV, Lewicki, J., Glogowski, E., Floyd, W. C., Valdez, C. A., Smith, W. L., Satcher, J. H. Jr., Bourcier, W. L., Spadaccini, C. M., Lewis, J. A. & Aines, R. D. 2015 Encapsulated liquid sorbents for carbon dioxide capture. Nature Commun. 6, 6124.Google Scholar
Von Kerczek, C. H. 1982 The instability of oscillatory plane Poiseuille flow. J. Fluid Mech. 116, 91–114.Google Scholar
Walter, A., Rehage, H. & Leonhard, H. 2001 Shear induced deformation of microcapsules: shape oscillations and membrane folding. Colloid Surf. 183–185, 123–132.Google Scholar
Wang, Z., Sui, Y., Spelt, P. D. M. & Wang, W. 2013 Three-dimensional dynamics of oblate and prolate capsules in shear flow. Phys. Rev. E 88, 053021.Google Scholar
Zhao, H., Isfahani, A. H. G., Olson, L. & Freund, J. B. 2010 A spectral boundary integral method for micro-circulatory cellular flows. J. Comput. Phys. 229, 3726–3744.Google Scholar
Zhao, H. & Shaqfeh, E. S. G. 2013 The shape stability of a lipid vesicle in a uniaxial extensional flow. J. Fluid Mech. 719, 345–361.Google Scholar