Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T18:03:27.622Z Has data issue: false hasContentIssue false
  • English
  • Français

Flexibility in flapping foil suppresses meandering of induced jet in absence of free stream

Published online by Cambridge University Press:  19 September 2014

Sachin Y. Shinde  and
Jaywant H. Arakeri
Sachin Y. Shinde
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560012, India
Jaywant H. Arakeri*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Thrust-generating flapping foils are known to produce jets inclined to the free stream at high Strouhal numbers 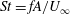$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{St} = fA/U_{\infty }$, where 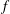$f$ is the frequency and 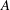$A$ is the amplitude of flapping and 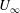$U_{\infty }$ is the free-stream velocity. Our experiments, in the limiting case of 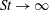$\mathit{St} \rightarrow \infty $ (zero free-stream speed), show that a purely oscillatory pitching motion of a chordwise flexible foil produces a coherent jet composed of a reverse Bénard–Kármán vortex street along the centreline, albeit over a specific range of effective flap stiffnesses. We obtain flexibility by attaching a thin flap to the trailing edge of a rigid NACA0015 foil; length of flap is 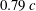$0.79\, c$ where $c$ is rigid foil chord length. It is the time-varying deflections of the flexible flap that suppress the meandering found in the jets produced by a pitching rigid foil for zero free-stream condition. Recent experiments (Marais et al., J. Fluid Mech., vol. 710, 2012, p. 659) have also shown that the flexibility increases the 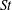$\mathit{St}$ at which non-deflected jets are obtained. Analysing the near-wake vortex dynamics from flow visualization and particle image velocimetry (PIV) measurements, we identify the mechanisms by which flexibility suppresses jet deflection and meandering. A convenient characterization of flap deformation, caused by fluid–flap interaction, is through a non-dimensional ‘effective stiffness’, 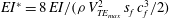$EI^{*} = 8 \, EI/(\rho \, V_{{{TE_{{max}}}}}^2 \, s_{{{f}}} \, c_{{{f}}}^3/2)$, representing the inverse of the flap deflection due to the fluid-dynamic loading; here, 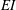$EI$ is the bending stiffness of flap, 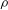$\rho $ is fluid density, 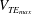$V_{{{TE_{{max}}}}}$ is the maximum velocity of rigid foil trailing edge, 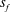$s_{{{f}}}$ is span and 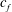$c_{{{f}}}$ is chord length of the flexible flap. By varying the amplitude and frequency of pitching, we obtain a variation in 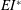$EI^{*}$ over nearly two orders of magnitude and show that only moderate 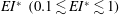$EI^{*}\ (0.1 \lesssim EI^{*} \lesssim 1)$ generates a sustained, coherent, orderly jet. Relatively ‘stiff’ flaps (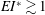$EI^{*} \gtrsim 1$), including the extreme case of no flap, produce meandering jets, whereas highly ‘flexible’ flaps (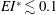$EI^{*} \lesssim 0.1$) produce spread-out jets. Obtained from the measured mean velocity fields, we present values of thrust coefficients for the cases for which orderly jets are observed.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Propulsion
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 231 - 250
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore 560064, India.

References

Anderson, J. M., Streitlien, K., Barrett, D. S. & Triantafyllou, M. S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.Google Scholar
Bohl, D. G. & Koochesfahani, M. M. 2009 MTV measurements of the vortical field in the wake of an airfoil oscillating at high reduced frequency. J. Fluid Mech. 620, 63–88.Google Scholar
Cleaver, D. J., Wang, Z. & Gursul, I. 2012 Bifurcating flows of plunging aerofoils at high Strouhal numbers. J. Fluid Mech. 708, 349–376.Google Scholar
Dabiri, J. O. 2005 On the estimation of swimming and flying forces from wake measurements. J. Expl Biol. 208, 3519–3532.CrossRefGoogle ScholarPubMed
Daniel, T. L. & Combes, S. A. 2002 Flexible wings and fins: Bending by inertial or fluid-dynamic forces? Integr. Compar. Biol. 42, 1044–1049.Google Scholar
Das, P., Govardhan, R. N. & Arakeri, J. H. 2013 Effect of hinged leaflets on vortex pair generation. J. Fluid Mech. 730, 626–658.Google Scholar
Dewey, P. A., Boschitsch, B. M., Moored, K. W., Stone, H. A. & Smits, A. J. 2013 Scaling laws for the thrust production of flexible pitching panels. J. Fluid Mech. 732, 29–46.Google Scholar
Dewey, P. A., Carriou, A. & Smits, A. J. 2012 On the relationship between efficiency and wake structure of a batoid-inspired oscillating fin. J. Fluid Mech. 691, 245–266.CrossRefGoogle Scholar
Eldredge, J. D., Toomey, J. & Medina, A. 2010 On the roles of chord-wise flexibility in a flapping wing with hovering kinematics. J. Fluid Mech. 659, 94–115.Google Scholar
von Ellenrieder, K. D. & Pothos, S. 2008 PIV measurements of the asymmetric wake of a two-dimensional heaving hydrofoil. Exp. Fluids 44, 733–745.Google Scholar
Ellington, C. P. 1984 The aerodynamics of hovering insect flight. III. Kinematics. Phil. Trans. R. Soc. Lond. B 305, 41–78.Google Scholar
Freymuth, P. 1990 Thrust generation by an airfoil in hover modes. Exp. Fluids 9, 17–24.CrossRefGoogle Scholar
Godoy-Diana, R., Aider, J. & Wesfreid, J. E. 2008 Transition in the wake of a flapping foil. Phys. Rev. E 77, 0163081.Google Scholar
Godoy-Diana, R., Marais, C., Aider, J. & Wesfreid, J. E. 2009 A model for the symmetry breaking of the reverse Bénard–von Kármán vortex street produced by a flapping foil. J. Fluid Mech. 622, 23–32.Google Scholar
Gustafson, K., Leben, R. & McArthur, J. 1992 Lift and thrust generation by an airfoil in hover modes. Comput. Fluid Dyn. J. 1, 47–57.Google Scholar
Heathcote, S. & Gursul, I. 2007 Jet switching phenomenon for a periodically plunging airfoil. Phys. Fluids 19, 0271041.Google Scholar
Heathcote, S., Martin, D. & Gursul, I. 2004 Flexible flapping airfoil propulsion at zero freestream velocity. AIAA J. 42, 2196–2204.CrossRefGoogle Scholar
Kang, C. K., Aono, H., Cesnik, C. E. S. & Shyy, W. 2011 Effects of flexibility on the aerodynamic performance of flapping wings. J. Fluid Mech. 689, 32–74.Google Scholar
Lai, J. C. S. & Platzer, M. F. 2001 Characteristics of a plunging airfoil at zero freestream velocity. AIAA J. 39, 531–534.Google Scholar
Lewin, G. C. & Haj-Hariri, H. 2003 Modelling thrust generation of a two-dimensional heaving airfoil in a viscous flow. J. Fluid Mech. 492, 339–362.Google Scholar
Marais, C., Thiria, B., Wesfreid, J. E. & Godoy-Diana, R. 2012 Stabilizing effect of flexibility in the wake of a flapping foil. J. Fluid Mech. 710, 659–669.Google Scholar
Shinde, S. Y.2012 Creation of an orderly jet and thrust generation in quiescent fluid from an oscillating two-dimensional flexible foil. PhD thesis, Indian Institute of Science, Bangalore, India, Department of Mechanical Engineering.Google Scholar
Shinde, S. Y. & Arakeri, J. H. 2013 Jet meandering by a foil pitching in quiescent fluid. Phys. Fluids 25, 041701.Google Scholar
Shukla, S., Govardhan, R. N. & Arakeri, J. H. 2013 Dynamics of a flexible splitter plate in the wake of a circular cylinder. J. Fluids Struct. 41, 127–134.Google Scholar
Shyy, W., Aono, H., Chimakurthi, S. K., Trizila, P., Kang, C. K., Cesnik, C. E. S. & Liu, H. 2010 Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 46, 284–327.Google Scholar
Shyy, W., Berg, M. & Ljungqvist, D. 1999 Flapping and flexible wings for biological and micro air vehicles. Prog. Aerosp. Sci. 35, 455–505.Google Scholar
Triantafyllou, M. S., Techet, A. H. & Hover, F. S. 2004 Review of experimental work in biomimetic foils. IEEE J. Ocean. Engng 29, 585–594.CrossRefGoogle Scholar
Triantafyllou, M. S., Triantafyllou, G. S. & Yue, D. K. P. 2000 Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 32, 33–53.Google Scholar
Wang, Z. J. 2000 Two-dimensional mechanism for insect hovering. Phys. Rev. Lett. 85, 2216–2219.CrossRefGoogle Scholar
Wootton, R. J. 1999 Invertebrate paraxial locomotory appendages: design, deformation and control. J. Expl Biol. 202, 3333–3345.Google Scholar
Supplementary material: File

Download undefined(File)
File 50.3 KB

Shinde Supplementary Movie

This video shows the dye visualization in a horizontal plane along the mid-span for the airfoil with flexible flap over 10 oscillation cycles (for amplitude of oscillation ±15°, and frequency 2 Hz). The rigid airfoil chord is 38 mm and flexible flap chord is 30 mm. Laser sheet is passed from bottom side of the visualization window. The transparent flap is blackened in the plane of visualization, except for a 3 mm portion near the trailing edge to identify the start of the flap. Two large vortices, which eventually become part of the ‘reverse Benard-Karman vortex street’, along with a few smaller vortices are shed per oscillation cycle. Movie clearly shows the role of flexible flap in the formation of non-meandering unidirectional vortex jet aligned along the center-line. The vortices are shed at the appropriate space and appropriate phase of the cycle. Note also that a vortex once shed is pushed downstream by flap induced motion. The movement of a streak of dye present below the airfoil clearly shows the pulling of the fluid towards the airfoil and the flap. Note that, the movie clearly shows that the leading edge vortices are not generated by the pitching foil. The small ‘blobs’ of dye near the leading edge and also on the airfoil surface are not the vortices, but they are formed due to the following two reasons: one, intermittent release of dye from the dye port, and two, since the motion of fluid is small near the leading edge, the dye accumulates there. These ‘blobs’ of dye are eventually convected downstream by the flow.

Download Shinde Supplementary Movie(Video)
Video 9.5 MB