Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T05:36:49.710Z Has data issue: false hasContentIssue false
  • English
  • Français

The first open channel for yield-stress fluids in porous media

Published online by Cambridge University Press:  03 February 2021

Dimitrios Fraggedakis Open the ORCID record for Dimitrios Fraggedakis [Opens in a new window] ,
Emad Chaparian Open the ORCID record for Emad Chaparian [Opens in a new window]  and
Outi Tammisola Open the ORCID record for Outi Tammisola [Opens in a new window]
Dimitrios Fraggedakis*
Affiliation:
Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA02139, USA
Emad Chaparian
Affiliation:
Mathematics Department, University of British Columbia, Vancouver, BCV6T 1Z2, Canada
Outi Tammisola
Affiliation:
Linné FLOW centre, Department of Engineering Mechanics, KTH Royal Institute of Technology, SE-10044Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

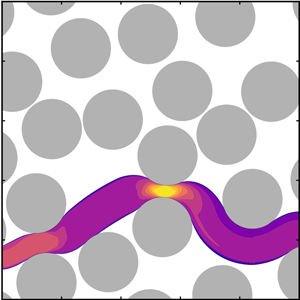
The prediction of the first fluidized path of yield-stress fluids in complex porous media is a challenging yet important task to understand the fundamentals of fluid flow in several industrial and biological processes. In most cases, the conditions that open this first path are known either through experiments or expensive computations. Here, we present a simple network model to predict the first open channel for a yield-stress fluid in a porous medium. For porous media made of non-overlapping discs, we find that the pressure drop ${\rm \Delta} P_c$ required to open the first channel for a given yield stress $\tau _y$ depends on both the relative discs size $R_s$ to the macroscopic length $L$ of the system and the packing fraction $\phi$. The non-dimensional pressure gradient ${\rm \Delta} P_c R_s/ \tau _y L$ (i.e. the critical yield number), however, depends on the packing fraction $\phi$ only, leading to a mastercurve for all examined ratios of $R_s/L$. In the case of non-overlapping discs, we find ${\rm \Delta} P_c R_s/ \tau _y L\sim \phi /(1-\phi )$. We also report the statistics on the arclength of the first open path. Finally, we discuss the implication of our results for the design of porous media used in energy storage applications.

JFM classification

Low-Reynolds-number flows: Porous media Non-Newtonian Flows: Plastic materials
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 911 , 25 March 2021 , A58
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Al-Kharusi, A.S. & Blunt, M.J. 2007 Network extraction from sandstone and carbonate pore space images. J. Petrol. Sci. Engng 56 (4), 219–231.CrossRefGoogle Scholar
Alim, K., Parsa, S., Weitz, D.A. & Brenner, M.P. 2017 Local pore size correlations determine flow distributions in porous media. Phys. Rev. Lett. 119 (14), 144501.CrossRefGoogle ScholarPubMed
Aufrecht, J.A., Fowlkes, J.D., Bible, A.N., Morrell-Falvey, J., Doktycz, M.J. & Retterer, S.T. 2019 Pore-scale hydrodynamics influence the spatial evolution of bacterial biofilms in a microfluidic porous network. PLoS ONE 14 (6), e0218316.CrossRefGoogle Scholar
Balhoff, M. 2005 Modeling the flow of non-Newtonian fluids in packed beds at the pore scale. PhD thesis, Louisiana State University.Google Scholar
Balhoff, M., Sanchez-Rivera, D., Kwok, A., Mehmani, Y. & Prodanović, M. 2012 Numerical algorithms for network modeling of yield stress and other non-Newtonian fluids in porous media. Transp. Porous Med. 93 (3), 363–379.CrossRefGoogle Scholar
Balhoff, M.T. & Thompson, K.E. 2004 Modeling the steady flow of yield-stress fluids in packed beds. AIChE J. 50 (12), 3034–3048.CrossRefGoogle Scholar
Balmforth, N.J., Frigaard, I.A. & Ovarlez, G. 2014 Yielding to stress: recent developments in viscoplastic fluid mechanics. Annu. Rev. Fluid Mech. 46, 121–146.CrossRefGoogle Scholar
Barenblatt, G.I., Entov, V.M. & Ryzhik, V.M. 1989 Theory of Fluid Flows through Natural Rocks. Kluwer Academic Publishers.Google Scholar
Bauer, D., Talon, L., Peysson, Y., Ly, H.B., Batôt, G., Chevalier, T. & Fleury, M. 2019 Experimental and numerical determination of Darcy's law for yield stress fluids in porous media. Phys. Rev. Fluids 4 (6), 063301.CrossRefGoogle Scholar
Blunt, M.J. 2001 Flow in porous media—pore-network models and multiphase flow. Curr. Opin. Colloid Interface Sci. 6 (3), 197–207.CrossRefGoogle Scholar
Blunt, M.J., Bijeljic, B., Dong, H., Gharbi, O., Iglauer, S., Mostaghimi, P., Paluszny, A. & Pentland, C. 2013 Pore-scale imaging and modelling. Adv. Water Resour. 51, 197–216.CrossRefGoogle Scholar
Bollobás, B. 2013 Modern Graph Theory, vol. 184. Springer Science & Business Media.Google Scholar
Bonn, D. & Denn, M.M. 2009 Yield stress fluids slowly yield to analysis. Science 324 (5933), 1401–1402.CrossRefGoogle Scholar
Bryant, S.L., King, P.R. & Mellor, D.W. 1993 Network model evaluation of permeability and spatial correlation in a real random sphere packing. Transp. Porous Med. 11 (1), 53–70.CrossRefGoogle Scholar
Chaparian, E., Izbassarov, D., De Vita, F., Brandt, L. & Tammisola, O. 2020 Yield-stress fluids in porous media: a comparison of viscoplastic and elastoviscoplastic flows. Meccanica 55 (2), 331–342.CrossRefGoogle ScholarPubMed
Chaparian, E. & Tammisola, O. 2021 Sliding flows of yield-stress fluids. Accepted for publication in J. Fluid Mech. (preprint) arXiv:2004.02950.CrossRefGoogle Scholar
Chen, M., Rossen, W. & Yortsos, Y.C. 2005 The flow and displacement in porous media of fluids with yield stress. Chem. Engng Sci. 60 (15), 4183–4202.CrossRefGoogle Scholar
Cule, D. & Torquato, S. 1999 Generating random media from limited microstructural information via stochastic optimization. J. Appl. Phys. 86 (6), 3428–3437.CrossRefGoogle Scholar
De Groot, S.R. & Mazur, P. 1984 Non-Equilibrium Thermodynamics. Dover Publication Inc.Google Scholar
Dijkstra, E.W. 1959 A note on two problems in connexion with graphs. Numer. Math. 1 (1), 269–271.CrossRefGoogle Scholar
Dimakopoulos, Y., Makrigiorgos, G., Georgiou, G.C. & Tsamopoulos, J. 2018 The PAL (Penalized Augmented Lagrangian) method for computing viscoplastic flows: a new fast converging scheme. J. Non-Newtonian Fluid Mech. 256, 23–41.CrossRefGoogle Scholar
Dimakopoulos, Y., Pavlidis, M. & Tsamopoulos, J. 2013 Steady bubble rise in Herschel–Bulkley fluids and comparison of predictions via the augmented Lagrangian method with those via the Papanastasiou model. J. Non-Newtonian Fluid Mech. 200, 34–51.CrossRefGoogle Scholar
Dimitriou, C.J. & McKinley, G.H. 2019 A canonical framework for modeling elasto-viscoplasticity in complex fluids. J. Non-Newtonian Fluid Mech. 265, 116–132.CrossRefGoogle Scholar
Dong, H. & Blunt, M.J. 2009 Pore-network extraction from micro-computerized-tomography images. Phys. Rev. E 80 (3), 036307.CrossRefGoogle ScholarPubMed
Duduta, M., Ho, B., Wood, V.C., Limthongkul, P., Brunini, V.E., Carter, W.C. & Chiang, Y. 2011 Semi-solid lithium rechargeable flow battery. Adv. Energy Mater. 1 (4), 511–516.CrossRefGoogle Scholar
Entov, V.M. 1967 On some two-dimensional problems of the theory of filtration with a limiting gradient. Prikl. Mat. Mekh. 31 (5), 820–833.Google Scholar
Farajzadeh, R., Andrianov, A., Krastev, R., Hirasaki, G.J. & Rossen, W.R. 2012 Foam–oil interaction in porous media: implications for foam assisted enhanced oil recovery. Adv. Colloid Interface Sci. 183, 1–13.CrossRefGoogle ScholarPubMed
Fatt, I. 1956 The network model of porous media. Trans. AIME 207 (1), 144–181.CrossRefGoogle Scholar
Fraggedakis, D., Dimakopoulos, Y. & Tsamopoulos, J. 2016 a Yielding the yield-stress analysis: a study focused on the effects of elasticity on the settling of a single spherical particle in simple yield-stress fluids. Soft Matt. 12 (24), 5378–5401.CrossRefGoogle ScholarPubMed
Fraggedakis, D., Dimakopoulos, Y. & Tsamopoulos, J. 2016 b Yielding the yield stress analysis: a thorough comparison of recently proposed elasto-visco-plastic (EVP) fluid models. J. Non-Newtonian Fluid Mech. 236, 104–122.CrossRefGoogle Scholar
Fraggedakis, D., Kouris, C., Dimakopoulos, Y. & Tsamopoulos, J. 2015 Flow of two immiscible fluids in a periodically constricted tube: transitions to stratified, segmented, churn, spray, or segregated flow. Phys. Fluids 27 (8), 082102.CrossRefGoogle Scholar
Frigaard, I.A. 2019 Background lectures on ideal visco-plastic fluid flows. In Lectures on Visco-Plastic Fluid Mechanics, pp. 1–40. Springer.CrossRefGoogle Scholar
Frigaard, I.A. & Nouar, C. 2005 On the usage of viscosity regularisation methods for visco-plastic fluid flow computation. J. Non-Newtonian Fluid Mech. 127 (1), 1–26.CrossRefGoogle Scholar
Frigaard, I.A., Paso, K.G. & de Souza Mendes, P.R. 2017 Bingham's model in the oil and gas industry. Rheol. Acta 56 (3), 259–282.CrossRefGoogle Scholar
Glowinski, R. 2008 Lectures on Numerical Methods for Non-Linear Variational Problems. Springer Science & Business Media.Google Scholar
Glowinski, R. & Wachs, A. 2011 On the numerical simulation of viscoplastic fluid flow. In Handbook of Numerical Analysis, vol. 16, pp. 483–717. Elsevier.CrossRefGoogle Scholar
Gostick, J.T. 2017 Versatile and efficient pore network extraction method using marker-based watershed segmentation. Phys. Rev. E 96 (2), 023307.CrossRefGoogle ScholarPubMed
Gostick, J.T., Khan, Z.A., Tranter, T.G., Kok, M.D.R., Agnaou, M., Sadeghi, M. & Jervis, R. 2019 Porespy: a python toolkit for quantitative analysis of porous media images. J. Open Source Softw. 4 (37), 1296.CrossRefGoogle Scholar
Green, D.W. & Willhite, G.P. 1998 Enhanced Oil Recovery, vol. 6. Society of Petroleum Engineers.Google Scholar
Greenkorn, R.A. 1983 Flow Phenomena in Porous Media: Fundamentals and Applications in Petroleum, Water and Food Production. Marcel Dekker.Google Scholar
Guo, P. 2012 Dependency of tortuosity and permeability of porous media on directional distribution of pore voids. Transp. Porous Med. 95 (2), 285–303.CrossRefGoogle Scholar
Gurtin, M.E., Fried, E. & Anand, L. 2010 The Mechanics and Thermodynamics of Continua. Cambridge University Press.CrossRefGoogle Scholar
Hagberg, A., Swart, P. & Chult, D.S. 2008 Exploring network structure, dynamics, and function using NetworkX. Tech. Rep. Los Alamos National Laboratory (LANL).Google Scholar
Hecht, F. 2012 New development in freefem++. J. Numer. Math. 20 (3), 251–265.CrossRefGoogle Scholar
Henkelman, G., Uberuaga, B.P. & Jónsson, H. 2000 A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113 (22), 9901–9904.CrossRefGoogle Scholar
Herzig, J.P., Leclerc, D.M. & Goff, P.L. 1970 Flow of suspensions through porous media–application to deep filtration. Ind. Engng Chem. Res. 62 (5), 8–35.CrossRefGoogle Scholar
Hestenes, M.R. 1969 Multiplier and gradient methods. J. Optim. Theor. Applics. 4 (5), 303–320.CrossRefGoogle Scholar
Hewitt, D.R., Daneshi, M., Balmforth, N.J. & Martinez, D.M. 2016 Obstructed and channelized viscoplastic flow in a Hele-Shaw cell. J. Fluid Mech. 790, 173–204.CrossRefGoogle Scholar
Hill, R. 1998 The Mathematical Theory of Plasticity, vol. 11. Oxford University Press.Google Scholar
Huilgol, R.R. 2015 Fluid Mechanics of Viscoplasticity. Springer.CrossRefGoogle Scholar
Jaisi, D.P., Saleh, N.B., Blake, R.E. & Elimelech, M. 2008 Transport of single-walled carbon nanotubes in porous media: filtration mechanisms and reversibility. Environ. Sci. Technol. 42 (22), 8317–8323.CrossRefGoogle ScholarPubMed
Kharabaf, H. & Yortsos, Y.C. 1997 Invasion percolation with memory. Phys. Rev. E 55 (6), 7177.CrossRefGoogle Scholar
Lester, D.R., Metcalfe, G. & Trefry, M.G. 2013 Is chaotic advection inherent to porous media flow? Phys. Rev. Lett. 111 (17), 174101.CrossRefGoogle ScholarPubMed
Liu, C., De Luca, A., Rosso, A. & Talon, L. 2019 Darcy's law for yield stress fluids. Phys. Rev. Lett. 122 (24), 245502.CrossRefGoogle ScholarPubMed
Mewis, J. & Wagner, N.J. 2012 Colloidal Suspension Rheology. Cambridge University Press.Google Scholar
Pandey, A. 2003 Solid-state fermentation. Biochem. Engng J. 13 (2–3), 81–84.CrossRefGoogle Scholar
Papanastasiou, T.C. 1987 Flows of materials with yield. J. Rheol. 31 (5), 385–404.CrossRefGoogle Scholar
Powell, M.J.D. 1978 Algorithms for nonlinear constraints that use Lagrangian functions. Math. Program. 14 (1), 224–248.CrossRefGoogle Scholar
Ronellenfitsch, H. & Dunkel, J. 2019 Chiral topological phases in designed mechanical networks. Front. Phys. 7, 178.CrossRefGoogle Scholar
Roquet, N. & Saramito, P. 2003 An adaptive finite element method for Bingham fluid flows around a cylinder. Comput. Meth. Appl. Mech. Engng 192 (31), 3317–3341.CrossRefGoogle Scholar
Roustaei, A., Chevalier, T., Talon, L. & Frigaard, I.A. 2016 Non-darcy effects in fracture flows of a yield stress fluid. J. Fluid Mech. 805, 222–261.CrossRefGoogle Scholar
Roustaei, A. & Frigaard, I.A. 2015 Residual drilling mud during conditioning of uneven boreholes in primary cementing. Part 2: steady laminar inertial flows. J. Non-Newtonian Fluid Mech. 226, 1–15.CrossRefGoogle Scholar
Sahimi, M. 2011 Flow and Transport in Porous Media and Fractured Rock: From Classical Methods to Modern Approaches. John Wiley & Sons.CrossRefGoogle Scholar
Saramito, P. 2007 A new constitutive equation for elastoviscoplastic fluid flows. J. Non-Newtonian Fluid Mech. 145 (1), 1–14.CrossRefGoogle Scholar
Saramito, P. 2016 Complex Fluids. Springer.CrossRefGoogle Scholar
Saramito, P. & Wachs, A. 2017 Progress in numerical simulation of yield stress fluid flows. Rheol. Acta 56 (3), 211–230.CrossRefGoogle Scholar
Schlesinger, W.H. 1999 Carbon sequestration in soils. Science 284 (5423), 2095.CrossRefGoogle Scholar
Silin, D. & Patzek, T. 2006 Pore space morphology analysis using maximal inscribed spheres. Phys. A 371 (2), 336–360.CrossRefGoogle Scholar
Sochi, T. 2005 Pore-scale modeling of non-Newtonian flow in porous media. PhD thesis, Imperial College London.Google Scholar
Stoop, N., Waisbord, N., Kantsler, V., Heinonen, V., Guasto, J.S. & Dunkel, J. 2019 Disorder-induced topological transition in porous media flow networks. J. Non-Newtonian Fluid Mech. 268, 66–74.CrossRefGoogle Scholar
Sun, H., Zhu, J., Baumann, D., Peng, L., Xu, Y., Shakir, I., Huang, Y. & Duan, X. 2019 Hierarchical 3D electrodes for electrochemical energy storage. Nat. Rev. Mater. 4 (1), 45–60.CrossRefGoogle Scholar
Talon, L., Auradou, H., Pessel, M. & Hansen, A. 2013 Geometry of optimal path hierarchies. Europhys. Lett. 103 (3), 30003.CrossRefGoogle Scholar
Talon, L. & Hansen, A. 2020 Effective rheology of bi-viscous non-Newtonian fluids in porous media. Front. Phys. 7, 225.CrossRefGoogle Scholar
Tien, C. & Payatakes, A.C. 1979 Advances in deep bed filtration. AIChE J. 25 (5), 737–759.CrossRefGoogle Scholar
Tjaden, B., Cooper, S.J., Brett, D.J.L., Kramer, D. & Shearing, P.R. 2016 On the origin and application of the bruggeman correlation for analysing transport phenomena in electrochemical systems. Curr. Opin. Chem. Engng 12, 44–51.CrossRefGoogle Scholar
Torquato, S. 1995 Nearest-neighbor statistics for packings of hard spheres and disks. Phys. Rev. E 51 (4), 3170.CrossRefGoogle ScholarPubMed
Torquato, S. & Haslach, H.W. Jr. 2002 Random heterogeneous materials: microstructure and macroscopic properties. Appl. Mech. Rev. 55 (4), B62–B63.CrossRefGoogle Scholar
Torquato, S., Lu, B. & Rubinstein, J. 1990 Nearest-neighbor distribution functions in many-body systems. Phys. Rev. A 41 (4), 2059.CrossRefGoogle ScholarPubMed
Torquato, S., Uche, O.U. & Stillinger, F.H. 2006 Random sequential addition of hard spheres in high Euclidean dimensions. Phys. Rev. E 74 (6), 061308.CrossRefGoogle ScholarPubMed
Tsamopoulos, J., Dimakopoulos, Y., Chatzidai, N., Karapetsas, G. & Pavlidis, M. 2008 Steady bubble rise and deformation in Newtonian and viscoplastic fluids and conditions for bubble entrapment. J. Fluid Mech. 601, 123–164.CrossRefGoogle Scholar
Waisbord, N., Stoop, N., Walkama, D.M., Dunkel, J. & Guasto, J.S. 2019 Anomalous percolation flow transition of yield stress fluids in porous media. Phys. Rev. Fluids 4 (6), 063303.CrossRefGoogle Scholar
Wei, T., Fan, F.Y., Helal, A., Smith, K.C., McKinley, G.H., Chiang, Y. & Lewis, J.A. 2015 Biphasic electrode suspensions for li-ion semi-solid flow cells with high energy density, fast charge transport, and low-dissipation flow. Adv. Energy Mater. 5 (15), 1500535.CrossRefGoogle Scholar
Zhang, G. & Torquato, S. 2013 Precise algorithm to generate random sequential addition of hard hyperspheres at saturation. Phys. Rev. E 88 (5), 053312.CrossRefGoogle ScholarPubMed
Zhu, Y., et al. . 2020 High-energy and high-power Zn-Ni flow batteries with semi-solid electrodes. Sustain. Energy Fuels 4, 4076.CrossRefGoogle Scholar