Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Alemi Ardakani, H.
Bridges, T.J.
and
Turner, M.R.
2012.
Resonance in a model for Cooker’s sloshing experiment.
European Journal of Mechanics - B/Fluids,
Vol. 36,
Issue. ,
p.
25.
Mayer, H. C.
and
Krechetnikov, R.
2012.
Walking with coffee: Why does it spill?.
Physical Review E,
Vol. 85,
Issue. 4,
Turner, M. R.
Bridges, T. J.
and
Ardakani, H. Alemi
2013.
Dynamic coupling in Cooker's sloshing experiment with baffles.
Physics of Fluids,
Vol. 25,
Issue. 11,
Weidman, Patrick D.
and
Herczynski, Andrzej
2013.
Fluid Dynamics in Physics, Engineering and Environmental Applications.
p.
41.
Turner, M. R.
and
Bridges, T. J.
2013.
Nonlinear energy transfer between fluid sloshing and vessel motion.
Journal of Fluid Mechanics,
Vol. 719,
Issue. ,
p.
606.
Sirwah, Magdy A.
2014.
Sloshing waves in a heated viscoelastic fluid layer in an excited rectangular tank.
Physics Letters A,
Vol. 378,
Issue. 45,
p.
3289.
Bouscasse, B.
Colagrossi, A.
Souto-Iglesias, A.
and
Cercos-Pita, J. L.
2014.
Mechanical energy dissipation induced by sloshing and wave breaking in a fully coupled angular motion system. II. Experimental investigation.
Physics of Fluids,
Vol. 26,
Issue. 3,
Turner, M.R.
Alemi Ardakani, H.
and
Bridges, T.J.
2015.
Instability of sloshing motion in a vessel undergoing pivoted oscillations.
Journal of Fluids and Structures,
Vol. 52,
Issue. ,
p.
166.
Ohayon, R.
and
Soize, C.
2015.
Vibration of structures containing compressible liquids with surface tension and sloshing effects. Reduced-order model.
Computational Mechanics,
Vol. 55,
Issue. 6,
p.
1071.
Sauret, A.
Boulogne, F.
Cappello, J.
Dressaire, E.
and
Stone, H. A.
2015.
Damping of liquid sloshing by foams.
Physics of Fluids,
Vol. 27,
Issue. 2,
Alemi Ardakani, H.
Bridges, T.J.
and
Turner, M.R.
2015.
Dynamic coupling between horizontal vessel motion and two-layer shallow-water sloshing.
Journal of Fluids and Structures,
Vol. 59,
Issue. ,
p.
432.
Weidman, Patrick
and
Turner, M.R.
2016.
Experiments on the synchronous sloshing in suspended containers described by shallow-water theory.
Journal of Fluids and Structures,
Vol. 66,
Issue. ,
p.
331.
Turner, M. R.
and
Weidman, Patrick
2016.
Coupled sloshing in hyperbolic containers suspended as a bifilar pendulum.
Physical Review Fluids,
Vol. 1,
Issue. 4,
Zhang, Chongwei
2016.
Analytical Study of Transient Coupling between Vessel Motion and Liquid Sloshing in Multiple Tanks.
Journal of Engineering Mechanics,
Vol. 142,
Issue. 7,
Bukreev, V. I.
2016.
Water surface waves in a horizontally oscillating container.
Journal of Applied Mechanics and Technical Physics,
Vol. 57,
Issue. 2,
p.
231.
Turner, M.R.
2016.
Liquid sloshing in a horizontally forced vessel with bottom topography.
Journal of Fluids and Structures,
Vol. 64,
Issue. ,
p.
1.
Kulczycki, Tadeusz
Kwaśnicki, Mateusz
and
Siudeja, Bartłomiej
2016.
The shape of the fundamental sloshing mode in axisymmetric containers.
Journal of Engineering Mathematics,
Vol. 99,
Issue. 1,
p.
157.
Huang, Y. H.
and
Turner, M. R.
2017.
Dynamic fluid sloshing in a one-dimensional array of coupled vessels.
Physical Review Fluids,
Vol. 2,
Issue. 12,
Hari, Megna
and
Sarigul-Klijn, Nesrin
2019.
Predicting Sloshing Motion in Flexible Propellant Tanks using Three-Dimensional Computational Simulation and Experimental Validation.
Zakaria, Kadry
Sirwah, Magdy A.
Elmorabie, Khaled M.
and
Eldeen, Shaker Nour
2019.
Sloshing waves in electrified fluid layers in an excited rectangular container.
Applied Ocean Research,
Vol. 91,
Issue. ,
p.
101902.
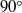 apex angles, and cylindrical annuli. It is assumed that the rectilinear horizontal motion of the containers is frictionless. The study focuses on measurements of the horizontal oscillations of these containers arising solely from the liquid waves excited within. While the wedge and cone exhibit only one mode of oscillation, the boxes, cylinders and annuli have an infinite number of modes. For the boxes, cylinders and one of the annuli, we have been able to excite motion and record data for both the first and second modes of oscillation. Frequencies
apex angles, and cylindrical annuli. It is assumed that the rectilinear horizontal motion of the containers is frictionless. The study focuses on measurements of the horizontal oscillations of these containers arising solely from the liquid waves excited within. While the wedge and cone exhibit only one mode of oscillation, the boxes, cylinders and annuli have an infinite number of modes. For the boxes, cylinders and one of the annuli, we have been able to excite motion and record data for both the first and second modes of oscillation. Frequencies 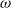 were acquired as the average of three experimental determinations for every filling of mass
were acquired as the average of three experimental determinations for every filling of mass 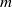 in the dry containers of mass
in the dry containers of mass 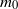 . Measurements of the dimensionless frequencies
. Measurements of the dimensionless frequencies 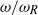 over a range of dimensionless liquid masses
over a range of dimensionless liquid masses 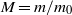 are found to be in essential agreement with theoretical predictions. The frequencies
are found to be in essential agreement with theoretical predictions. The frequencies 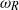 used for normalization arise naturally in the mathematical analysis, different for each geometry considered. Free surface waveforms for a box, a cylinder, the wedge and the cone are compared at a fixed value of
used for normalization arise naturally in the mathematical analysis, different for each geometry considered. Free surface waveforms for a box, a cylinder, the wedge and the cone are compared at a fixed value of 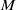 .
.