Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-20T08:38:24.624Z Has data issue: false hasContentIssue false
  • English
  • Français

Experiments on standing bubbles in a vertical pipe

Published online by Cambridge University Press:  10 December 2008

GENNARO DELLO IOIO  and
ANDREW W. WOODS
GENNARO DELLO IOIO
Affiliation:
BP Institute, University of Cambridge, Cambridge, CB3 0EZ, UK
ANDREW W. WOODS
Affiliation:
BP Institute, University of Cambridge, Cambridge, CB3 0EZ, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a series of laboratory experiments in which a steady stream of air is supplied through a small hole in the wall of a vertical pipe of rectangular cross-section down which there is a steady flux of water. For a range of liquid flow rates, the air forms a steady standing bubble whose nose is attached to the point of air supply. The steady bubble sheds a flux of much smaller air bubbles at its base, located downstream of the air injection point. The minimum liquid speed for which steady standing bubbles develop occurs at a particular Froude number of the liquid flow, Frd = U/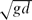 = 0.38, where U is the upstream speed, g the acceleration due to gravity and d the width of the cell. These trapped bubbles are distinct from the freely rising Taylor bubble, in that the Froude number at the nose is variable. Also, on a length scale greater than that influenced by surface tension, we find that the bubble nose asymptotes to a cusp-like shape, with an angle that decreases with Frd. We show that numerical solutions of the potential flow equations replicate the bubble shape and angle of the cusp, which appear independent of the gas flux. We also find that there is a minimum gas flux for which these standing bubbles develop. As the gas flux decreases below this threshold, the standing bubbles become unstable and, instead, a much shorter oscillating bubble develops. This produces a wake which has similarities with that formed downstream of a cylinder in a confined channel, but which also carries bubbles downstream. We also find that with sufficiently small gas flux, no bubble develops. For liquid flow rates smaller than the critical value, Frd < 0.38, we find that the bubbles become unstable and detach from the injection point and rise up the tube.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 616 , 10 December 2008 , pp. 31 - 41
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2005 Controlled oscillations of a cylinder: forces and wake modes. J. Fluid Mech. 538, 31–69.CrossRefGoogle Scholar
Clanet, C., Héraud, P. & Searby, G. 2004 On the motion of bubbles in vertical tubes of arbitrary cross-sections: some complements to the Dumitrescu–Taylor problem. J. Fluid Mech. 519, 359–376.CrossRefGoogle Scholar
Collins, R., De Moraes, F. F., Davidson, J. F. & Harrison, D. 1978 The motion of a large gas bubble rising through liquid flowing in a tube. J. Fluid Mech. 89, 497–514.CrossRefGoogle Scholar
Dake, L. P. 1979 Fundamentals of Reservoir Engineering. Elsevier.Google Scholar
Davies, R. M. & Taylor, G. I. 1950 The mechanics of large bubbles rising through extended liquids and through liquids in tube. Proc. R. Soc. Lond. A 200, 375–390.Google Scholar
Deniz, S. & Staubli, Th. 1997 Oscillating rectangular and octagonal profiles: interaction of leading- and trailing-edge vortex formation. J. Fluids Struct. 11, 3–31.CrossRefGoogle Scholar
Dumitrescu, D. T. 1943 Ströming an einer luftblase im senkrechten rohr. Z. Angew. Math. Mech. 23, 139–149.CrossRefGoogle Scholar
Hiwada, M. & Mabuchi, I. 1981 Flow behaviour and heat transfer around the circular cylinder at high blockage ratios. Heat Transfer Japan Res. 10, 17–39.Google Scholar
Keller, J. B. & Geer, J. 1973 Flow of thin streams with free boundaries. J. Fluid Mech. 59, 417–432.CrossRefGoogle Scholar
Rao, S. S. 1999 The Finite Element Method in Engineering 3rd edn.Butterworth-Heinemann.Google Scholar
Rhee, C. W., Talbot, L., Sethian, J. A. 1995 Dynamical behaviour of a premixed turbulent open V-flame. J. Fluid Mech. 300, 87–115.CrossRefGoogle Scholar
Richter, A. & Naudascher, E. 1976 Fluctuating forces on a rigid circular cylinder in confined flow. J. Fluid Mech. 78, 561–576.CrossRefGoogle Scholar
Roshko, A. 1954 On the drag and shedding frequency of two-dimensional bluff bodies. NACA Tech. Note 3169.Google Scholar
Vanden-Broeck, J. 1984 a Bubbles rising in a tube and jets falling from a nozzle. Phys. Fluids 27 (5), 1090–1093.CrossRefGoogle Scholar
Vanden-Broeck, J. 1984 b Rising bubbles in a two-dimensional tube with surface tension. Phys. Fluids 27 (11), 2604–2607.CrossRefGoogle Scholar
Vanden-Broeck, J. 1984 c Numerical solutions for cavitating flow of a fluid with surface tension past a curved obstacle. Phys. Fluids 27 (11), 2601–2603.CrossRefGoogle Scholar
Wegener, P. P. & Parlange, J. Y. 1973 Spherical cap bubbles. Annu. Rev. Fluid Mech. 5, 79–100.CrossRefGoogle Scholar