Published online by Cambridge University Press: 19 February 2018
This study investigates the mean flow structure of two shock-wave boundary-layer interactions generated by moderately swept compression ramps in a Mach 2 flow. The ramps have a compression angle of either 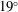 $19^{\circ }$ or
$19^{\circ }$ or 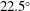 $22.5^{\circ }$ and a sweep angle of
$22.5^{\circ }$ and a sweep angle of 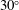 $30^{\circ }$. The primary diagnostic methods used for this study are surface-streakline flow visualization and particle image velocimetry. The shock-wave boundary-layer interactions are shown to be quasi-conical, with the intermittent region, separation line and reattachment line all scaling in a self-similar manner outside of the inception region. This is one of the first studies to investigate the flow field of a swept ramp using particle image velocimetry, allowing more sensitive measurements of the velocity flow field than previously possible. It is observed that the streamwise velocity component outside of the separated flow reaches the quasi-conical state at the same time as the bulk surface flow features. However, the streamwise and cross-stream components within the separated flow take longer to recover to the quasi-conical state, which indicates that the inception region for these low-magnitude velocity components is actually larger than was previously assumed. Specific scaling laws reported previously in the literature are also investigated and the results of this study are shown to scale similarly to these related interactions. Certain limiting cases of the scaling laws are explored that have potential implications for the interpretation of cylindrical and quasi-conical scaling.
$30^{\circ }$. The primary diagnostic methods used for this study are surface-streakline flow visualization and particle image velocimetry. The shock-wave boundary-layer interactions are shown to be quasi-conical, with the intermittent region, separation line and reattachment line all scaling in a self-similar manner outside of the inception region. This is one of the first studies to investigate the flow field of a swept ramp using particle image velocimetry, allowing more sensitive measurements of the velocity flow field than previously possible. It is observed that the streamwise velocity component outside of the separated flow reaches the quasi-conical state at the same time as the bulk surface flow features. However, the streamwise and cross-stream components within the separated flow take longer to recover to the quasi-conical state, which indicates that the inception region for these low-magnitude velocity components is actually larger than was previously assumed. Specific scaling laws reported previously in the literature are also investigated and the results of this study are shown to scale similarly to these related interactions. Certain limiting cases of the scaling laws are explored that have potential implications for the interpretation of cylindrical and quasi-conical scaling.
In the original version of this article Mustafa Nail Musta’s name was misspelled. A notice detailing this has been published (doi:http://dx.doi.org/10.1017/jfm.2018.243) and the error rectified in the online PDF and HTML versions.
Please note a has been issued for this article.