Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Deike, Luc
Pizzo, Nick
and
Melville, W. Kendall
2017.
Lagrangian transport by breaking surface waves.
Journal of Fluid Mechanics,
Vol. 829,
Issue. ,
p.
364.
Longo, Sandro
Clavero, Maria
Chiapponi, Luca
and
Losada, Miguel
2017.
Invariants of Turbulence Reynolds Stress and of Dissipation Tensors in Regular Breaking Waves.
Water,
Vol. 9,
Issue. 11,
p.
893.
Zheng, Peng
Li, Ming
van der A, Dominic A.
van der Zanden, Joep
Wolf, Judith
Chen, Xueen
and
Wang, Caixia
2017.
A 3D unstructured grid nearshore hydrodynamic model based on the vortex force formalism.
Ocean Modelling,
Vol. 116,
Issue. ,
p.
48.
Smith, Lisa
Kolaas, Jostein
Jensen, Atle
and
Sveen, Kristian
2018.
Investigation of surface structures in two phase wavy pipe flow by utilizing X-ray tomography.
International Journal of Multiphase Flow,
Vol. 107,
Issue. ,
p.
246.
Wang, Jinghua
Ma, Qingwei
and
Yan, Shiqiang
2018.
A fully nonlinear numerical method for modeling wave–current interactions.
Journal of Computational Physics,
Vol. 369,
Issue. ,
p.
173.
van den Bremer, T. S.
and
Breivik, Ø.
2018.
Stokes drift.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 376,
Issue. 2111,
p.
20170104.
Paprota, Maciej
and
Sulisz, Wojciech
2018.
Particle trajectories and mass transport under mechanically generated nonlinear water waves.
Physics of Fluids,
Vol. 30,
Issue. 10,
Weber, Jan Erik H.
and
Christensen, Kai H.
2019.
Virtual wave stress and transient mean drift in spatially damped long interfacial waves.
European Journal of Mechanics - B/Fluids,
Vol. 77,
Issue. ,
p.
162.
Herterich, James G.
and
Dias, Frédéric
2019.
Extreme long waves over a varying bathymetry.
Journal of Fluid Mechanics,
Vol. 878,
Issue. ,
p.
481.
Myrhaug, Dag
Wang, Hong
and
Holmedal, Lars Erik
2019.
Addendum to “Stokes transport in layers in the water column based on long-term wind statistics: assessment using long-term wave statistics”.
Oceanologia,
Vol. 61,
Issue. 4,
p.
522.
Pizzo, Nick
Melville, W. Kendall
and
Deike, Luc
2019.
Lagrangian Transport by Nonbreaking and Breaking Deep-Water Waves at the Ocean Surface.
Journal of Physical Oceanography,
Vol. 49,
Issue. 4,
p.
983.
van den Bremer, T. S.
Whittaker, C.
Calvert, R.
Raby, A.
and
Taylor, P. H.
2019.
Experimental study of particle trajectories below deep-water surface gravity wave groups.
Journal of Fluid Mechanics,
Vol. 879,
Issue. ,
p.
168.
Paprota, M.
2019.
Particle Image Velocimetry Measurements of Standing Wave Kinematics in Vicinity of a Rigid Vertical Wall.
Instruments and Experimental Techniques,
Vol. 62,
Issue. 2,
p.
277.
Calvert, R.
Whittaker, C.
Raby, A.
Taylor, P. H.
Borthwick, A. G. L.
and
van den Bremer, T. S.
2019.
Laboratory study of the wave-induced mean flow and set-down in unidirectional surface gravity wave packets on finite water depth.
Physical Review Fluids,
Vol. 4,
Issue. 11,
Lenain, Luc
Pizzo, Nick
and
Melville, W. Kendall
2019.
Laboratory studies of Lagrangian transport by breaking surface waves.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
Lindgren, Georg
and
Prevosto, Marc
2020.
Wave asymmetry and particle orbits in irregular wave models.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Wang, Z.
Guan, X.
and
Vanden-Broeck, J.-M.
2020.
Progressive flexural–gravity waves with constant vorticity.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Paprota, Maciej
2020.
Experimental Study on Spatial Variation of Mass Transport Induced by Surface Waves Generated in a Finite-Depth Laboratory Flume.
Journal of Physical Oceanography,
Vol. 50,
Issue. 12,
p.
3501.
Higgins, C.
Vanneste, J.
and
van den Bremer, T. S.
2020.
Unsteady Ekman‐Stokes Dynamics: Implications for Surface Wave‐Induced Drift of Floating Marine Litter.
Geophysical Research Letters,
Vol. 47,
Issue. 18,
van Sebille, Erik
Aliani, Stefano
Law, Kara Lavender
Maximenko, Nikolai
Alsina, José M
Bagaev, Andrei
Bergmann, Melanie
Chapron, Bertrand
Chubarenko, Irina
Cózar, Andrés
Delandmeter, Philippe
Egger, Matthias
Fox-Kemper, Baylor
Garaba, Shungudzemwoyo P
Goddijn-Murphy, Lonneke
Hardesty, Britta Denise
Hoffman, Matthew J
Isobe, Atsuhiko
Jongedijk, Cleo E
Kaandorp, Mikael L A
Khatmullina, Liliya
Koelmans, Albert A
Kukulka, Tobias
Laufkötter, Charlotte
Lebreton, Laurent
Lobelle, Delphine
Maes, Christophe
Martinez-Vicente, Victor
Morales Maqueda, Miguel Angel
Poulain-Zarcos, Marie
Rodríguez, Ernesto
Ryan, Peter G
Shanks, Alan L
Shim, Won Joon
Suaria, Giuseppe
Thiel, Martin
van den Bremer, Ton S
and
Wichmann, David
2020.
The physical oceanography of the transport of floating marine debris.
Environmental Research Letters,
Vol. 15,
Issue. 2,
p.
023003.
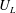 $U_{L}$, and the Lagrangian excess period,
$U_{L}$, and the Lagrangian excess period, 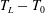 $T_{L}-T_{0}$, where
$T_{L}-T_{0}$, where 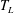 $T_{L}$ is the Lagrangian period and
$T_{L}$ is the Lagrangian period and 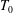 $T_{0}$ the Eulerian linear period, are obtained by particle tracking velocimetry (PTV) in non-breaking periodic laboratory waves at a finite water depth of
$T_{0}$ the Eulerian linear period, are obtained by particle tracking velocimetry (PTV) in non-breaking periodic laboratory waves at a finite water depth of 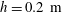 $h=0.2~\text{m}$, wave height of
$h=0.2~\text{m}$, wave height of 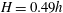 $H=0.49h$ and wavenumber of
$H=0.49h$ and wavenumber of 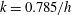 $k=0.785/h$. Both
$k=0.785/h$. Both 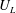 $U_{L}$ and
$U_{L}$ and 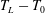 $T_{L}-T_{0}$ are functions of the average vertical position of the paths,
$T_{L}-T_{0}$ are functions of the average vertical position of the paths, 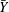 $\bar{Y}$, where
$\bar{Y}$, where 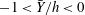 $-1<\bar{Y}/h<0$. The functional relationships
$-1<\bar{Y}/h<0$. The functional relationships 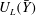 $U_{L}(\bar{Y})$ and
$U_{L}(\bar{Y})$ and 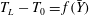 $T_{L}-T_{0}=f(\bar{Y})$ are very similar. Comparisons to calculations by the inviscid strongly nonlinear Fenton method and the second-order theory show that the streaming velocities in the boundary layers below the wave surface and above the fluid bottom contribute to a strongly enhanced forward drift velocity and excess period. The experimental drift velocity shear becomes more than twice that obtained by the Fenton method, which again is approximately twice that of the second-order theory close to the surface. There is no mass flux of the periodic experimental waves and no pressure gradient. The results from a total number of 80 000 experimental particle paths in the different phases and vertical positions of the waves show a strong collapse. The particle paths are closed at the two vertical positions where
$T_{L}-T_{0}=f(\bar{Y})$ are very similar. Comparisons to calculations by the inviscid strongly nonlinear Fenton method and the second-order theory show that the streaming velocities in the boundary layers below the wave surface and above the fluid bottom contribute to a strongly enhanced forward drift velocity and excess period. The experimental drift velocity shear becomes more than twice that obtained by the Fenton method, which again is approximately twice that of the second-order theory close to the surface. There is no mass flux of the periodic experimental waves and no pressure gradient. The results from a total number of 80 000 experimental particle paths in the different phases and vertical positions of the waves show a strong collapse. The particle paths are closed at the two vertical positions where 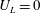 $U_{L}=0$.
$U_{L}=0$.


