Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-17T17:58:12.664Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation on compressible flow over a circular cylinder at Reynolds number of between 1000 and 5000

Published online by Cambridge University Press:  21 April 2020

T. Nagata Open the ORCID record for T. Nagata [Opens in a new window] ,
A. Noguchi ,
K. Kusama ,
T. Nonomura Open the ORCID record for T. Nonomura [Opens in a new window] ,
A. Komuro Open the ORCID record for A. Komuro [Opens in a new window] ,
A. Ando  and
K. Asai
T. Nagata*
Affiliation:
Department of Aerospace Engineering, Tohoku University, 6-6-01, Aramaki, Aoba-ku, Sendai, Miyagi, 980-8579, Japan
A. Noguchi
Affiliation:
Department of Aerospace Engineering, Tohoku University, 6-6-01, Aramaki, Aoba-ku, Sendai, Miyagi, 980-8579, Japan
K. Kusama
Affiliation:
Department of Aerospace Engineering, Tohoku University, 6-6-01, Aramaki, Aoba-ku, Sendai, Miyagi, 980-8579, Japan
T. Nonomura
Affiliation:
Department of Aerospace Engineering, Tohoku University, 6-6-01, Aramaki, Aoba-ku, Sendai, Miyagi, 980-8579, Japan
A. Komuro
Affiliation:
Department of Electrical Engineering, Tohoku University, 6-6-05, Aramaki, Aoba-ku, Sendai, Miyagi, 980-8579, Japan
A. Ando
Affiliation:
Department of Electrical Engineering, Tohoku University, 6-6-05, Aramaki, Aoba-ku, Sendai, Miyagi, 980-8579, Japan
K. Asai
Affiliation:
Department of Aerospace Engineering, Tohoku University, 6-6-01, Aramaki, Aoba-ku, Sendai, Miyagi, 980-8579, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

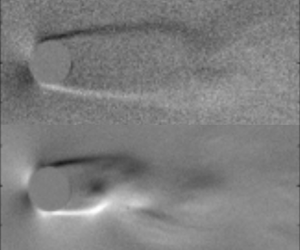
In the present study, a compressible low-Reynolds-number flow over a circular cylinder was investigated using a low-density wind tunnel with time-resolved schlieren visualizations and pressure and force measurements. The Reynolds number ($Re$) based on freestream quantities and the diameter of a circular cylinder was set to be between 1000 and 5000, and the freestream Mach number ($M$) between 0.1 and 0.5. As a result, we have clarified the effect of $M$ on the aerodynamic characteristics of flow over a circular cylinder at $Re=O(10^{3})$. The results of the schlieren visualization showed that the trend of $M$ effect on the flow field, that are the release location of the Kármán vortices, the Strouhal number of vortex shedding and the maximum width of the recirculation, is changed at approximately $Re=3000$. In addition, the spanwise phase difference of the surface pressure fluctuation was captured by the measurement using pressure-sensitive paint at approximately $Re=3000$ of higher-$M$ cases. The observed spanwise phase difference is considered to relate to the spanwise phase difference of the vortex shedding due to the oblique instability wave on the separated shear layer caused by the compressibility effects. The Strouhal number of the vortex shedding is influenced by $M$ and $Re$, and those effects are nonlinear. However, the effects of $M$ and $Re$ can approximately be characterized by the maximum width of the recirculation. In addition, the $M$ effect on the drag coefficient can be characterized by the maximum width of the recirculation region and the Prandtl–Glauert transformation.

JFM classification

Wakes/Jets: Vortex streets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 893 , 25 June 2020 , A13
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anyoji, M., Nose, K., Ida, S., Numata, D., Nagai, H. & Asai, K. 2011 Development of a low-density wind tunnel for simulating martian atmospheric flight. Trans. Japan Soc. Aeronaut. Space Sci. 9, 21–27.Google Scholar
Behara, S. & Mittal, S. 2010 Wake transition in flow past a circular cylinder. Phys. Fluids 22 (11), 114104.CrossRefGoogle Scholar
Bogdanoff, D. W. 1983 Compressibility effects in turbulent shear layers. AIAA J. 21 (6), 926–927.CrossRefGoogle Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.CrossRefGoogle Scholar
Canuto, D. & Taira, K. 2015 Two-dimensional compressible viscous flow around a circular cylinder. J. Fluid Mech. 785, 349–371.CrossRefGoogle Scholar
Coutanceau, M. & Bouard, R. 1977 Experimental determination of the main features of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow. J. Fluid Mech. 79 (2), 231–256.CrossRefGoogle Scholar
Delany, N. K. & Sorensen, N. E.1953 Low-speed drag of cylinders of various shapes. Tech. Rep. NACA-TN-3038. National Advisory Committee for Aeronautics.Google Scholar
Dennis, S. C. R. & Chang, G.-Z. 1970 Numerical solutions for steady flow past a circular cylinder at Reynolds numbers up to 100. J. Fluid Mech. 42 (3), 471–489.CrossRefGoogle Scholar
Dyment, A. & Gryson, P.1979 Study of turbulent subcritical and supercritical flows by high-speed visualisation. AGARD Paper, Vol. 28, pp. 1–28.Google Scholar
Feng, X., Xie, Y., Song, M., Yu, W. & Tang, J. 2018 Fast randomized pca for sparse data. Proc. Mach. Learn. Res. 95, 710–725.Google Scholar
Gerrard, J. H. 1961 An experimental investigation of the oscillating lift and drag of a circular cylinder shedding turbulent vortices. J. Fluid Mech. 11 (2), 244–256.CrossRefGoogle Scholar
Glauert, H. 1928 The effect of compressibility on the lift of an aerofoil. Proc. R. Soc. Lond. Ser. A 118 (779), 113–119.Google Scholar
Gowen, F. E. & Perkins, E. W.1953 Drag of circular cylinders for a wide range of Reynolds numbers and Mach numbers. Tech. Rep. NACA-TN-2960. National Advisory Committee for Aeronautics.Google Scholar
Hall, D. W., Parks, R. W. & Morris, S.1997 Airplane for mars exploration: conceptual design of the full-scale vehicle design, construction and test of performance and deployment models. Report submitted to NASA Ames Research Center by Dvid Hall Consulting (available at www.redpeace.org/Propulsoin.pdf).Google Scholar
Inokuchi, H., Tanaka, H. & Ando, T. 2009 Development of an onboard doppler lidar for flight safety. J. Aircraft 46 (4), 1411–1415.CrossRefGoogle Scholar
Kitchens, C. W. & Bush, C. C. 1972 Low Reynolds number flow past a transverse cylinder at mach two. AIAA J. 10 (10), 1381–1382.CrossRefGoogle Scholar
Knowler, A. E. & Pruden, F. W. 1944 On the Drag of Circular Cylinders at High Speeds. HM Stationery Office.Google Scholar
Lindsey, W. F.1938 Drag of cylinders of simple shapes. Tech. Rep. NACA-TN-3038. National Advisory Committee for Aeronautics.Google Scholar
McCarthy, J. F. & Kubota, T. 1964 A study of wakes behind a circular cylinder at m = 5. 7. AIAA J. 2 (4), 629–636.CrossRefGoogle Scholar
Meliga, P., Sipp, D. & Chomaz, J.-M. 2010 Effect of compressibility on the global stability of axisymmetric wake flows. J. Fluid Mech. 660, 499–526.CrossRefGoogle Scholar
Murthy, V. & Rose, W. 1977 Form drag, skin friction, and vortex shedding frequencies for subsonic and transonic crossflows on circular cylinder. In 10th Fluid and Plasmadynamics Conference, p. 687. American Institute of Aeronautics and Astronautics.Google Scholar
Murthy, V. S. & Rose, W. C. 1978 Detailed measurements on a circular cylinder in cross flow. AIAA J. 16 (6), 549–550.CrossRefGoogle Scholar
Nagata, T., Noguchi, A., Nonomura, T., Ohtani, K. & Asai, K. 2019 Experimental investigation of transonic and supersonic flow over a sphere for Reynolds numbers of 103–105 by free-flight tests with schlieren visualization. Shock Waves 30, 139–151.CrossRefGoogle Scholar
Nagata, T., Nonomura, T., Takahashi, S. & Fukuda, K.Direct numerical simulation of subsonic, transonic and supersonic flow over an isolated sphere up to a Reynolds number of 1000. J. Fluid Mech. (under review).Google Scholar
Nagata, T., Nonomura, T., Takahashi, S., Mizuno, Y. & Fukuda, K. 2016 Investigation on subsonic to supersonic flow around a sphere at low Reynolds number of between 50 and 300 by direct numerical simulation. Phys. Fluids 28 (5), 056101.CrossRefGoogle Scholar
Nagata, T., Nonomura, T., Takahashi, S., Mizuno, Y. & Fukuda, K. 2018a Direct numerical simulation of flow around a heated/cooled isolated sphere up to a Reynolds number of 300 under subsonic to supersonic conditions. Intl J. Heat Mass Transfer 120, 284–299.CrossRefGoogle Scholar
Nagata, T., Nonomura, T., Takahashi, S., Mizuno, Y. & Fukuda, K. 2018b Direct numerical simulation of flow past a sphere at a Reynolds number between 500 and 1000 in compressible flows. In 2018 AIAA Aerospace Sciences Meeting, p. 0381. American Institute of Aeronautics and Astronautics.Google Scholar
Nagata, T., Nonomura, T., Takahashi, S., Mizuno, Y. & Fukuda, K. 2018c Direct numerical simulation of flow past a transversely rotating sphere up to a Reynolds number of 300 in compressible flow. J. Fluid Mech. 857, 878–906.CrossRefGoogle Scholar
Norberg, C. 2001 Flow around a circular cylinder: aspects of fluctuating lift. J. Fluids Struct. 15 (3–4), 459–469.CrossRefGoogle Scholar
Papamoschou, D. & Roshko, A. 1988 The compressible turbulent shear layer: an experimental study. J. Fluid Mech. 197, 453–477.CrossRefGoogle Scholar
Riahi, H., Meldi, M., Favier, J., Serre, E. & Goncalves, E. 2018 A pressure-corrected immersed boundary method for the numerical simulation of compressible flows. J. Comput. Phys. 374, 361–383.CrossRefGoogle Scholar
Rodriguez, O. 1984 The circular cylinder in subsonic and transonic flow. AIAA J. 22 (12), 1713–1718.CrossRefGoogle Scholar
Roshko, A.1954 On the development of turbulent wakes from vortex streets. NACA-TR-1191.Google Scholar
Roshko, A. 1961 Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 10 (3), 345–356.CrossRefGoogle Scholar
Sakaue, H. 1999 Anodized aluminum pressure sensitive paint in a cryogenic wind tunnel. In ISA Proceedings of the 45th International Instrumentation Symposium, pp. 345–354. Instrument Society of America.Google Scholar
Sandham, N. D. & Reynolds, W. C. 1990 Compressible mixing layer-linear theory and direct simulation. AIAA J. 28 (4), 618–624.CrossRefGoogle Scholar
Sandham, N. D. & Reynolds, W. C. 1991 Three-dimensional simulations of large eddies in the compressible mixing layer. J. Fluid Mech. 224, 133–158.CrossRefGoogle Scholar
Sansica, A., Robinet, J.-C., Alizard, F. & Goncalves, E. 2018 Three-dimensional instability of a flow past a sphere: Mach evolution of the regular and Hopf bifurcations. J. Fluid Mech. 855, 1088–1115.CrossRefGoogle Scholar
Takada, H. 1975 Determination of the position of separation for the free-streamline flow past a circular cylinder. J. Phys. Soc. Japan 39 (1), 247–252.CrossRefGoogle Scholar
Taneda, S. 1956 Experimental investigation of the wakes behind cylinders and plates at low Reynolds numbers. J. Phys. Soc. Japan 11 (3), 302–307.CrossRefGoogle Scholar
Tritton, D. J. 1959 Experiments on the flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 6 (4), 547–567.CrossRefGoogle Scholar
Williamson, C. H. K. 1988a Defining a universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 31 (10), 2742–2744.CrossRefGoogle Scholar
Williamson, C. H. K. 1988b The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31 (11), 3165–3168.CrossRefGoogle Scholar
Xia, Z., Xiao, Z., Shi, Y. & Chen, S. 2016 Mach number effect of compressible flow around a circular cylinder. AIAA J. 2004–2009.CrossRefGoogle Scholar
Xu, C.-Y., Chen, L.-W. & Lu, X.-Y. 2009 Numerical simulation of shock wave and turbulence interaction over a circular cylinder. Mod. Phys. Lett. 23 (3), 233–236.CrossRefGoogle Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders: Volume 2: Applications, vol. 2. Oxford University Press.Google Scholar