Article contents
Experimental and theoretical study of dewetting corner flow
Published online by Cambridge University Press: 03 December 2014
Abstract
We study a partial dewetting corner flow with a moving contact line at a finite Reynolds number, 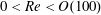 $0<\mathit{Re}<O(100)$. When the speed of the moving contact line increases, the receding contact line appears with a corner shape that is also observed in a gravity-driven liquid droplet on an incline and on a plate withdrawn from a bath. In the current problem,
$0<\mathit{Re}<O(100)$. When the speed of the moving contact line increases, the receding contact line appears with a corner shape that is also observed in a gravity-driven liquid droplet on an incline and on a plate withdrawn from a bath. In the current problem, 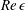 $\mathit{Re}\,{\it\epsilon}$ is larger than unity, where
$\mathit{Re}\,{\it\epsilon}$ is larger than unity, where  ${\it\epsilon}$ is the aspect ratio of the flow structure. Therefore, classical lubrication theory is no longer appropriate. We develop a modified three-dimensional lubrication model for the dewetting corner structure at
${\it\epsilon}$ is the aspect ratio of the flow structure. Therefore, classical lubrication theory is no longer appropriate. We develop a modified three-dimensional lubrication model for the dewetting corner structure at 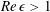 $\mathit{Re}\,{\it\epsilon}>1$ by taking into account the internal flow pattern and by scaling arguments. The key requirement is that the streamlines in the corner are straight and (nearly) parallel. In this case, we can obtain a modified pressure consisting of the capillary pressure and the dynamic pressure. This model describes the three-dimensional dewetting corner structure at the rear of the moving droplets at
$\mathit{Re}\,{\it\epsilon}>1$ by taking into account the internal flow pattern and by scaling arguments. The key requirement is that the streamlines in the corner are straight and (nearly) parallel. In this case, we can obtain a modified pressure consisting of the capillary pressure and the dynamic pressure. This model describes the three-dimensional dewetting corner structure at the rear of the moving droplets at 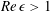 $\mathit{Re}\,{\it\epsilon}>1$ and furthermore shows that the dynamic pressure effects become dominant at a small half-opening angle. Additionally, this model provides analytical results for the internal flow, which is a self-similar flow pattern. To validate the analytical results, we perform high-speed shadowgraphy and tomographic particle image velocimetry (PIV). We find a good agreement between the theoretical and the experimental results.
$\mathit{Re}\,{\it\epsilon}>1$ and furthermore shows that the dynamic pressure effects become dominant at a small half-opening angle. Additionally, this model provides analytical results for the internal flow, which is a self-similar flow pattern. To validate the analytical results, we perform high-speed shadowgraphy and tomographic particle image velocimetry (PIV). We find a good agreement between the theoretical and the experimental results.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 9
- Cited by



