Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T11:40:00.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution, propagation and interactions with topography of hurricane-like vortices in a moist-convective rotating shallow-water model

Published online by Cambridge University Press:  10 September 2020

Masoud Rostami  and
Vladimir Zeitlin Open the ORCID record for Vladimir Zeitlin [Opens in a new window]
Masoud Rostami
Affiliation:
Laboratory of Dynamical Meteorology, Sorbonne University (SU), Ecole Normale Supérieure (ENS), CNRS, Paris75231, France Institute for Geophysics and Meteorology (IGM), University of Cologne, Cologne, Germany
Vladimir Zeitlin*
Affiliation:
Laboratory of Dynamical Meteorology, Sorbonne University (SU), Ecole Normale Supérieure (ENS), CNRS, Paris75231, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

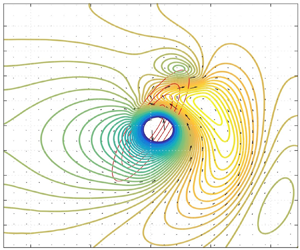
The so-called moist-convective shallow-water model, which incorporates moist convection in a simple albeit self-consistent way is used to analyse how intense localized vortices, with distributions of horizontal velocity and relative vorticity close to those observed in tropical cyclones (TC), evolve and interact with topography on the $\beta$-plane at low latitudes. Instabilities of such TC-like vortices are studied first in the $f$-plane approximation, and their development, interplay with beta-gyres and the role they play in vorticity redistribution and intensification are then analysed along the vortex trajectories on the $\beta$-plane, both in dry and moist-convective environments. Interactions of the vortices with an idealized topography in the form of zonal and meridional ridges and islands of elliptic form and the role of moist convection in these processes are then investigated, revealing rich vortex-dynamics patterns. The results can be helpful in crude analyses and predictions of the evolution of the barotropic component of TC, of their trajectories over the ocean and during landfall and of related condensation/precipitation patterns.

JFM classification

Convection: Moist convection Geophysical and Geological Flows: Topographic effects Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 902 , 10 November 2020 , A24
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adem, J. 1956 A series solution for the barotropic vorticity equation and its application in the study of atmospheric vortices. Tellus 8 (3), 364–372.CrossRefGoogle Scholar
Bouchut, F. 2007 Efficient numerical finite volume schemes for shallow water models. In Nonlinear Dynamics of Rotating Shallow Water: Methods and Advances (ed. Zeitlin, V.), chap. 4, Edited Series on Advances in Nonlinear Science and Complexity, vol. 2, pp. 189–256. Elsevier.CrossRefGoogle Scholar
Bouchut, F., Lambaerts, J., Lapeyre, G. & Zeitlin, V. 2009 Fronts and nonlinear waves in a simplified shallow-water model of the atmosphere with moisture and convection. Phys. Fluids 21 (11), 116604.CrossRefGoogle Scholar
Carnevale, G. F., Kloosterziel, R. C. & van Heijst, G. J. F. 1991 Propagation of barotropic vortices over topography in a rotating tank. J. Fluid Mech. 233, 119–139.CrossRefGoogle Scholar
Chan, J. C. L. & Williams, R. T. 1987 Analytical and numerical studies of the beta-effect in tropical cyclone motion. Part 1. Zero mean flow. J. Atmos. Sci. 44 (9), 1257–1265.2.0.CO;2>CrossRefGoogle Scholar
Chang, C.-P., Yeh, T.-C. & Chen, J. M. 1993 Effects of terrain on the surface structure of typhoons over taiwan. Mon. Weath. Rev. 121 (3), 734–752.2.0.CO;2>CrossRefGoogle Scholar
Charney, J. G. & Eliassen, A. 1964 On the growth of the hurricane depression. J. Atmos. Sci. 21, 68–75.2.0.CO;2>CrossRefGoogle Scholar
Chavas, D. R. & Emanuel, K. 2014 Equilibrium tropical-cyclone size in the idealized state of radiative-convective equilibrium. J. Atmos. Sci. 71, 1663–1680.CrossRefGoogle Scholar
Cronin, T. W. & Chavas, D. 2019 Dry and semidry tropical cyclones. J. Atmos. Sci. 76, 2193–2212.Google Scholar
Cronin, T. W. & Emanuel, K. 2013 The climate time scale in the approach to radiative-convective equilibrium. J. Adv. Model. Earth Sys. 5, 843–849.CrossRefGoogle Scholar
Fiorino, M. & Elsberry, R. L. 1989 Some aspects of vortex structure related to tropical cyclone motion. J. Atmos. Sci. 46 (7), 975–990.2.0.CO;2>CrossRefGoogle Scholar
Flor, J.-B. & Eames, I. 2002 Dynamics of monopolar vortices on a topographic beta-plane. J. Fluid Mech. 456, 353–376.CrossRefGoogle Scholar
van Geffen, J. & Davies, P. 1999 Interaction of a monopolar vortex with a topographic ridge. Geophys. Astrophys. Fluid Dyn. 90, 1–41.CrossRefGoogle Scholar
Gill, A. 1982 a Atmosphere-Ocean Dynamics. Academic Press.Google Scholar
Gill, A. 1982 b Studies of moisture effects in simple atmospheric models: the stable case. Geophys. Astrophys. Fluid Dyn. 19, 119–152.CrossRefGoogle Scholar
Grimshaw, R., Broutman, D., He, X. & Sun, P. 1994 Analytical and numerical study of a barotropic eddy on a topographic slope. J. Phys. Oceanogr. 24, 1587–1607.2.0.CO;2>CrossRefGoogle Scholar
Hendricks, E. A., Schubert, W. H., Chen, Y.-H., Kuo, H.-C. & Peng, M. S. 2014 Hurricane eyewall evolution in a forced shallow-water model. J. Atmos. Sci. 71 (5), 1623–1643.CrossRefGoogle Scholar
Hinds, A., Johnson, E. & McDonald, N. 2016 Beach vortices near circular topography. Phys. Fluids 28 (10), 106602.CrossRefGoogle Scholar
Huang, C., Chen, C., Chen, S. & Nolan, D. S. 2016 On the upstream track deflection of tropical cyclones past a mountain range: idealized experiments. J. Atmos. Sci. 73, 3157–3180.CrossRefGoogle Scholar
Jones, R., Willoughby, H. & Montgomery, M. 2009 Alignment of hurricane-like vortices on f and beta-planes. J. Atmos. Sci. 66, 1779–1792.CrossRefGoogle Scholar
Katsaros, K. 2001 Evaporation and humidity. In Encyclopedia of Ocean Sciences (ed. Steele, J. H.), pp. 870–877. Academic Press.CrossRefGoogle Scholar
Kim, S.-H., Kwon, H. J. & Elsberry, R. L. 2009 Beta gyres in global analysis fields. Adv. Atmos. Sci. 26 (5), 984–994.CrossRefGoogle Scholar
Kossin, J., McNoldy, B. & Schubert, W. 2002 Vortical swirls in hurricane eye clouds. Mon. Weath. Rev. 130 (12), 3144–3149.2.0.CO;2>CrossRefGoogle Scholar
Kossin, J. & Schubert, W. 2001 Mesovortices, polygonal flow patterns, and rapid pressure falls in hurricane-like vortices. J. Atmos. Sci. 58, 2196–2209.2.0.CO;2>CrossRefGoogle Scholar
Kuo, H.-C., Williams, R. T., Chen, J.-H. & Chen, Y.-L. 2001 Topographic effects on barotropic vortex motion: no mean flow. J. Atmos. Sci. 58 (10), 1310–1327.2.0.CO;2>CrossRefGoogle Scholar
Lahaye, N. & Zeitlin, V. 2015 Centrifugal, barotropic and baroclinic instabilities of isolated ageostrophic anticyclones in the two-layer rotating shallow water model and their nonlinear saturation. J. Fluid Mech. 762, 5–34.CrossRefGoogle Scholar
Lahaye, N. & Zeitlin, V. 2016 Understanding instabilities of tropical cyclones and their evolution with a moist-convective rotating shallow-water model. J. Atmos. Sci. 73, 505–523.CrossRefGoogle Scholar
Lambaerts, J., Lapeyre, G., Zeitlin, V. & Bouchut, F. 2011 Simplified two-layer models of precipitating atmosphere and their properties. Phys. Fluids 23, 046603.CrossRefGoogle Scholar
Lee, C.-S., Liu, Y.-C. & Chien, F.-C. 2008 The secondary low and heavy rainfall associated with typhoon Mindulle (2004). Mon. Weath. Rev. 136 (4), 1260–1283.CrossRefGoogle Scholar
Li, X. & Wang, B. 1994 Barotropic dynamics of the beta gyres and beta drift. J. Atmos. Sci. 51 (5), 746–756.2.0.CO;2>CrossRefGoogle Scholar
Lin, Y., Chen, S. & Liu, L. 2016 Orographic influence on basic flow and cyclonic circulation and their impacts on track deflection of an idealized tropical cyclone. J. Atmos. Sci. 73, 3951–3974.CrossRefGoogle Scholar
Lin, Y.-L., Han, J., Hamilton, D. W. & Huang, C.-Y. 1999 Orographic influence on a drifting cyclone. J. Atmos. Sci. 56 (4), 534–562.2.0.CO;2>CrossRefGoogle Scholar
Liu, Y., Kurganov, A. & Zeitlin, V. 2020 Moist-convective thermal rotating shallow water model. Phys. Fluids 32, 066601.Google Scholar
Mallen, K. J., Montgomery, M. T. & Wang, B. 2005 Reexamining the near-core radial structure of the tropical cyclone primary circulation: implications for vortex resiliency. J. Atmos. Sci. 62 (2), 408–425.CrossRefGoogle Scholar
Matsuno, T. 1966 Quasi-geostrophic motions in the equatorial area. J. Met. Soc. Japan 44 (1), 25–43.CrossRefGoogle Scholar
McWilliams, J. C. & Flierl, G. R. 1979 On the evolution of isolated, nonlinear vortices. J. Phys. Oceanogr. 9 (6), 1155–1182.2.0.CO;2>CrossRefGoogle Scholar
Menelaou, K., Yau, M. & Martinez, Y. 2012 Impact of asymmetric dynamical processes on the structure and intensity change of two-dimensional hurricane-like annular vortices. J. Atmos. Sci. 70 (2), 559–582.CrossRefGoogle Scholar
Montgomery, M. & Smith, R. 2017 Recent developments in the fluid dynamics of tropical cyclones. Annu. Rev. Fluid Mech. 49, 541–574.CrossRefGoogle Scholar
Nolan, D. & Montgomery, M. 2002 Nonhydrostatic, three-dimensional perturbations to balanced hurricane-like vortices. Part 1. Linearized formulation, stability, and evolution. J. Atmos. Sci. 59 (21), 2989–3020.2.0.CO;2>CrossRefGoogle Scholar
Ooyama, K. 1964 A dynamical model for the study of tropical cyclone development. Geofis. Intern. 4, 187–198.Google Scholar
Ooyama, K. 1969 Numerical simulation of the life cycle of tropical cyclone. J. Atmos. Sci. 26, 3–40.2.0.CO;2>CrossRefGoogle Scholar
Reznik, G. M. 1992 Dynamics of singular vortices on a beta-plane. J. Fluid Mech. 240, 405–432.CrossRefGoogle Scholar
Reznik, G. M. & Dewar, W. 1994 An analytical theory of distributed axisymmetric barotropic vortices on the beta-plane. J. Fluid Mech. 269, 301–321.CrossRefGoogle Scholar
Reznik, G. M. & Grimshaw, R. 2001 Ageostrophic dynamics of an intense localized vortex on a beta-plane. J. Fluid Mech. 443, 351–376.CrossRefGoogle Scholar
Richardson, G. 2000 Vortex motion in shallow water with varying bottom topography and zero Froude number. J. Fluid Mech. 411, 351–374.CrossRefGoogle Scholar
Rostami, M. & Zeitlin, V. 2017 Influence of condensation and latent heat release upon barotropic and baroclinic instabilities of atmospheric vortices in a rotating shallow water model on the f-plane. Geophys. Astrophys. Fluid Dyn. 111, 1–31.CrossRefGoogle Scholar
Rostami, M. & Zeitlin, V. 2018 Improved moist-convective rotating shallow water model and its application to instabilities of hurricane-like vortices. Q. J. R. Meteorol. Soc. 144, 1450–1462.CrossRefGoogle Scholar
Rostami, M., Zeitlin, V. & Montabone, L. 2018 On the role of spatially inhomogeneous diabatic effects upon the evolution of Mars’ annular polar vortex. Icarus 314, 376–388.CrossRefGoogle Scholar
Rostami, M., Zeitlin, V. & Spiga, A. 2017 On the dynamical nature of Saturn's North polar hexagon. Icarus 297, 59–70.CrossRefGoogle Scholar
Rozoff, C. M., Kossin, J. P., Schubert, W. H. & Mulero, P. J. 2009 Internal control of hurricane intensity variability: the dual nature of potential vorticity mixing. J. Atmos. Sci. 66 (1), 133–147.CrossRefGoogle Scholar
Schecter, D. 2018 On the instabilities of tropical cyclones generated by cloud resolving models. Tellus A 70 (1), 1–30.CrossRefGoogle Scholar
Schecter, D. & Montgomery, M. 2007 Waves in a cloudy vortex. J. Atmos. Sci. 64, 314–337.CrossRefGoogle Scholar
Schecter, D. A. & Dunkerton, T. 2009 Hurricane formation in diabatic Ekman turbulence. Q. J. R. Meteorol. Soc. 135, 823–840.CrossRefGoogle Scholar
Schubert, W., Montgomery, M., Taft, R., Guinn, T., Fulton, S., Kossin, J. & Edwards, J. 1999 Polygonal eyewalls, asymmetric eye contraction, and potential vorticity mixing in hurricanes. J. Atmos. Sci. 56, 1197–1223.2.0.CO;2>CrossRefGoogle Scholar
Schubert, W., Slocum, C. J. & Taft, R. 2016 Forced, balanced model of tropical cyclone intensification. J. Met. Soc. Japan 94, 119–135.CrossRefGoogle Scholar
Smith, R. & Ulrich, W. 1990 An analytical theory of tropical cyclone motion using a barotropic model. J. Atmos. Sci. 47, 1973–1986.2.0.CO;2>CrossRefGoogle Scholar
Sutyrin, G. & Flierl, G. 1994 Intense vortex motionon the beta-plane: development of the beta gyres. J. Atmos Sci. 51, 773–790.2.0.CO;2>CrossRefGoogle Scholar
Tang, C. & Chan, J. 2015 Idealized simulations of the effect of local and remote topographies on tropical cyclones tracks. Q. J. R. Meteorol. Soc. 141, 2045–2056.CrossRefGoogle Scholar
Tang, C. & Chan, J. 2016 Idealized simulations of the effect of Taiwan topography on the tracks of tropical cyclones with different sizes. Q. J. R. Meteorol. Soc. 142, 793–804.CrossRefGoogle Scholar
Willoughby, H. E. 1994 Nonlinear motion of a shallow water barotropic vortex. J. Atmos. Sci. 51 (24), 3722–3744.2.0.CO;2>CrossRefGoogle Scholar
Wright, K. 1964 Chebyshev collocation methods for ordinary differential equations. Comput. J. 6 (4), 358–365.CrossRefGoogle Scholar
Wu, C., Li, T. & Huang, Y. 2015 Influence of mesoscale topography on tropical cyclone tracks: Further examination of the chanelling effect. J. Atmos. Sci. 72 (4), 3032–3050.CrossRefGoogle Scholar
Wu, C.-C. 2001 Numerical simulation of typhoon Gladys (1994) and its interaction with Taiwan terrain using the GFDL hurricane model. Mon. Weath. Rev. 129 (6), 1533–1549.2.0.CO;2>CrossRefGoogle Scholar
Yang, L., Fei, J., Huang, X., Cheng, X., Yang, X., Ding, J. & Shi, W. 2016 Asymmetric distribution of convection in tropical cyclones over the western North Pacific Ocean. Adv. Atmos. Sci. 33 (11), 1306–1321.CrossRefGoogle Scholar
Yeh, T.-C. & Elsberry, R. L. 1993 a Interaction of typhoons with the taiwan orography. Part 1. Upstream track deflections. Mon. Weath. Rev. 121 (12), 3193–3212.2.0.CO;2>CrossRefGoogle Scholar
Yeh, T.-C. & Elsberry, R. L. 1993 b Interaction of typhoons with the Taiwan orography. Part 2. Continuous and discontinuous tracks across the Island. Mon. Weath. Rev. 121 (12), 3213–3233.2.0.CO;2>CrossRefGoogle Scholar
Yeh, T.-C., Hsiao, L.-F., Chen, D.-S. & Huang, K.-N. 2012 A study on terrain-induced tropical cyclone looping in East Taiwan: case study of typhoon Haitang in 2005. Nat. Hazards 63 (3), 1497–1514.CrossRefGoogle Scholar
Zehnder, J. 1993 The influence of large-scale topography on barotropic vortex motion. J. Atmos. Sci. 50 (15), 2519–2532.2.0.CO;2>CrossRefGoogle Scholar
Zeitlin, V. 2018 Geophysical Fluid Dynamics: Understanding (almost) Everything with Rotating Shallow Water Models. Oxford University Press.CrossRefGoogle Scholar