Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T01:25:37.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of a turbulent cloud under rotation

Published online by Cambridge University Press:  02 September 2014

A. Ranjan  and
P. A. Davidson
A. Ranjan*
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
P. A. Davidson
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Localized patches of turbulence frequently occur in geophysics, such as in the atmosphere and oceans. The effect of rotation, 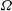$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\boldsymbol{\Omega}$, on such a region (a ‘turbulent cloud’) is governed by inhomogeneous dynamics. In contrast, most investigations of rotating turbulence deal with the homogeneous case, although inhomogeneous turbulence is more common in practice. In this paper, we describe the results of 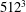$512^3$ direct numerical simulations (DNS) of a turbulent cloud under rotation at three Rossby numbers (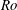$\mathit{Ro}$), namely 0.1, 0.3 and 0.5. Using a spatial filter, fully developed homogeneous turbulence is vertically confined to the centre of a periodic box before the rotation is turned on. Energy isosurfaces show that columnar structures emerge from the cloud and grow into the adjacent quiescent fluid. Helicity is used as a diagnostic and confirms that these structures are formed by inertial waves. In particular, it is observed that structures growing parallel to the rotation axis (upwards) have negative helicity and those moving antiparallel (downwards) to the axis have positive helicity, a characteristic typical of inertial waves. Two-dimensional energy spectra of horizontal wavenumbers, 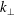$k_{\perp }$, versus dimensionless time, 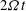$2 \varOmega t$, confirm that these columnar structures are wavepackets which travel at the group velocities of inertial waves. The kinetic energy transferred from the turbulent cloud to the waves is estimated using Lagrangian particle tracking to distinguish between turbulent and ‘wave-only’ regions of space. The amount of energy transferred to waves is 40 % of the initial at 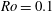$\mathit{Ro}=0.1$, while it is 16 % at 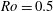$\mathit{Ro}=0.5$. In both cases the bulk of the energy eventually resides in the waves. It is evident from this observation that inertial waves can carry a significant portion of the energy away from a localized turbulent source and are therefore an efficient mechanism of energy dispersion.

JFM classification

Geophysical and Geological Flows: Rotating flows Turbulent Flows: Rotating turbulence Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 488 - 509
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartello, P., Métais, O. & Lesieur, M. 1994 Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 29, 1–29.Google Scholar
Bellet, F., Godeferd, F. S., Scott, J. F. & Cambon, C. 2006 Wave turbulence in rapidly rotating flows. J. Fluid Mech. 562, 83–121.CrossRefGoogle Scholar
Bordes, G., Moisy, F., Dauxois, T. & Cortet, P. 2012 Experimental evidence of a triadic resonance of plane inertial waves in a rotating fluid. Phys. Fluids 24 (1), 014105.Google Scholar
Cambon, C. & Jacquin, L. 1989 Spectral approach to non-isotropic turbulence subjected to rotation. J. Fluid Mech. 202, 295–317.Google Scholar
Cambon, C., Mansour, N. N. & Godeferd, F. S. 1997 Energy transfer in rotating turbulence. J. Fluid Mech. 337, 303–332.Google Scholar
Davidson, P. A. 2013 Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Davidson, P. A. 2014 The dynamics and scaling laws of planetary dynamos driven by inertial waves. Geophys. J. Int. 198, 1832–1847.CrossRefGoogle Scholar
Davidson, P. A., Staplehurst, P. J. & Dalziel, S. B. 2006 On the evolution of eddies in a rapidly rotating system. J. Fluid Mech. 557, 135–144.Google Scholar
Dickinson, S. C. & Long, R. R. 1983 Oscillating-grid turbulence including effects of rotation. J. Fluid Mech. 126, 315–333.CrossRefGoogle Scholar
Duran-Matute, M., Flor, J., Godeferd, F. & Jause-Labert, C. 2013 Turbulence and columnar vortex formation through inertial-wave focusing. Phys. Rev. E 87 (4), 041001.Google Scholar
Godeferd, F. S. & Lollini, L. 1999 Direct numerical simulations of turbulence with confinement and rotation. J. Fluid Mech. 393, 257–308.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Haine, T. W. H. & Cherian, D. A. 2013 Analogies of ocean/atmosphere rotating fluid dynamics with gyroscopes: teaching opportunities. Bull. Am. Meteorol. Soc. 94, 673–684.Google Scholar
Hopfinger, E. J., Browand, F. K. & Gagne, Y. 1982 Turbulence and waves in a rotating tank. J. Fluid Mech. 125, 505–534.Google Scholar
Jacquin, L., Leuchter, O., Cambon, C. & Mathieu, J. 1990 Homogeneous turbulence in the presence of rotation. J. Fluid Mech. 220, 1–52.Google Scholar
Kolvin, I., Cohen, K., Vardi, Y. & Sharon, E. 2009 Energy transfer by inertial waves during the buildup of turbulence in a rotating system. Phys. Rev. Lett. 102 (1), 1–4.CrossRefGoogle Scholar
Lighthill, M. J. 1967 On waves generated in dispersive systems by travelling forcing effects, with applications to the dynamics of rotating fluids. J. Fluid Mech. 27 (4), 725–752.Google Scholar
Lilly, D. K. 1986 The structure, energetics and propagation of rotating convective storms. Part II: helicity and storm stabilization. J. Atmos. Sci. 43, 126–140.Google Scholar
Maffioli, A., Davidson, P. A., Dalziel, S. B. & Swaminathan, N. 2014 The evolution of a stratified turbulent cloud. J. Fluid Mech. 739, 229–253.Google Scholar
Mininni, P. D. & Pouquet, A. 2010 Rotating helical turbulence. I. Global evolution and spectral behavior. Phys. Fluids 22, 035135.Google Scholar
Moffatt, H. K. 1970 Dynamo action associated with random inertial waves in a rotating conducting fluid. J. Fluid Mech. 44 (4), 705–719.Google Scholar
Nazarenko, S. V. & Schekochihin, A. A. 2011 Critical balance in magnetohydrodynamic, rotating and stratified turbulence: towards a universal scaling conjecture. J. Fluid Mech. 677, 134–153.Google Scholar
Olson, P. 2013 Experimental dynamos and the dynamics of planetary cores. Annu. Rev. Earth Planet. Sci. 41, 153–181.CrossRefGoogle Scholar
Pan, C. 2001 Gibbs phenomenon removal and digital filtering directly through the fast Fourier transform. IEEE Trans. Signal Process. 49 (2), 444–448.Google Scholar
Proudman, J. 1916 On the motion of solids in a liquid possessing vorticity. Proc. R. Soc. Lond. A 92, 408–424.Google Scholar
Rogallo, R. S.1981 Numerical experiments in homogeneous turbulence. Tech Rep. 81835. NASA Technical Memorandum.Google Scholar
Scott, J. F. 2014 Wave turbulence in a rotating channel. J. Fluid Mech. 741, 316–349.Google Scholar
Smith, L. M. & Lee, Y. 2005 On near resonances and symmetry breaking in forced rotating flows at moderate Rossby number. J. Fluid Mech. 535, 111–142.Google Scholar
Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11 (6), 1608–1622.Google Scholar
Staplehurst, P. J.2007 Structure formation in rotating turbulence. PhD thesis, Department of Engineering, University of Cambridge.Google Scholar
Staplehurst, P. J., Davidson, P. A. & Dalziel, S. B. 2008 Structure formation in homogeneous freely decaying rotating turbulence. J. Fluid Mech. 598, 81–105.Google Scholar
Taylor, G. I. 1921 Experiments with rotating fluids. Proc. R. Soc. Lond. A 100 (73), 114–121.Google Scholar
Thompson, R. O. R. Y. 1978 Observation of inertial waves in the stratosphere. Q. J. R. Meteorol. Soc. 104 (441), 691–698.Google Scholar
Veronis, G. 1970 The analogy between rotating and stratified fluids. Annu. Rev. Fluid Mech. 2, 37–66.Google Scholar
Waleffe, F. 1993 Inertial transfers in the helical decomposition. Phys. Fluids A 5 (3), 677–685.Google Scholar
Wilson, J. D., Thurtell, G. W. & Kidd, G. E. 1981 Numerical simulation of particle trajectories in inhomogeneous turbulence, II: systems with variable turbulent velocity scale. Boundary-Layer Meteorol. 21, 423–441.Google Scholar
Yeung, P. K. & Zhou, Y. 1998 Numerical study of rotating turbulence with external forcing. Phys. Fluids 10 (11), 2895–2909.Google Scholar
Yoshimatsu, K., Midorikawa, M. & Kaneda, Y. 2011 Columnar eddy formation in freely decaying homogeneous rotating turbulence. J. Fluid Mech. 677, 154–178.Google Scholar
Zhemin, T. & Rongsheng, W. 1994 Helicity dynamics of atmospheric flow. Adv. Atmos. Sci. 11 (2), 175–188.Google Scholar