Article contents
Estimating intermittency in three-dimensional Navier–Stokes turbulence
Published online by Cambridge University Press: 14 April 2009
Abstract
The issue of why computational resolution in Navier–Stokes turbulence is hard to achieve is addressed. Under the assumption that the three-dimensional Navier–Stokes equations have a global attractor it is nevertheless shown that solutions can potentially behave differently in two distinct regions of space–time 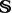 ± where
± where 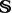 − is comprised of a union of disjoint space–time ‘anomalies’. If
− is comprised of a union of disjoint space–time ‘anomalies’. If 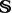 − is non-empty it is dominated by large values of |∇ω|, which is consistent with the formation of vortex sheets or tightly coiled filaments. The local number of degrees of freedom
− is non-empty it is dominated by large values of |∇ω|, which is consistent with the formation of vortex sheets or tightly coiled filaments. The local number of degrees of freedom 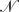 ± needed to resolve the regions in
± needed to resolve the regions in 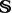 ± satisfies
± satisfies 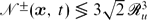 , where
, where 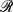 u = uL/ν is a Reynolds number dependent on the local velocity field u(x, t).
u = uL/ν is a Reynolds number dependent on the local velocity field u(x, t).
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2009
References
REFERENCES
- 3
- Cited by


