Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-27T02:33:43.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Energetics and mixing of thermally driven flows in Hele-Shaw cells

Published online by Cambridge University Press:  17 November 2021

Hugo N. Ulloa Open the ORCID record for Hugo N. Ulloa [Opens in a new window]  and
Juvenal A. Letelier Open the ORCID record for Juvenal A. Letelier [Opens in a new window]
Hugo N. Ulloa
Affiliation:
Department of Earth and Environmental Science, University of Pennsylvania, Philadelphia, PA 19104-6316, USA Physics of Aquatic Systems Laboratory (APHYS)-Margaretha Kamprad Chair, École Polytechnique Fédérale de Laussane, CH-1015 Lausanne, Switzerland
Juvenal A. Letelier*
Affiliation:
Departamento de Ingeniería Civil, Universidad de Chile, Avenida Blanco Encalada 2002, Santiago 8370449, Chile Centro de Excelencia en Geotermia de los Andes (ANID-FONDAP), Plaza Ercilla 803, Santiago 8370450, Chile
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

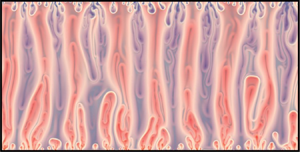
Thermally driven flows in fractures play a key role in enhancing the heat transfer and fluid mixing across the Earth's lithosphere. Yet the energy pathways in such confined environments have not been characterised. Building on Letelier et al. (J. Fluid Mech., vol. 864, 2019, pp. 746–767), we introduce novel expressions for energy transfer rates – energetics – of geometrically constrained Rayleigh–Bénard convection in Hele-Shaw cells (HS-RBC) based on two different conceptual frameworks. First, we derived the energetics following the well-established framework introduced by Winters et al. (J. Fluid Mech., vol. 289, 1995, pp. 115–128), in which the gravitational potential energy, $E_{\textit {p}}$, is decomposed into its available, $E_{\textit {ap}}$, and background, $E_{\textit {bp}}$, components. Secondly, we derived the energetics considering a new decomposition for $E_{\textit {p}}$, named dynamic, $E_{\textit {dp}}$, and reference, $E_{\textit {rp}}$, potential energies; $E_{\textit {dp}}$ is defined as the departure of the system's potential energy from the reference state $E_{\textit {rp}}$, determined by the ‘energy’ of the scalar fluctuations. For HS-RBC, both frameworks lead to the same energy transfer rates at a steady state, satisfying the relationship $\langle E_{\textit {ap}} \rangle _{\tau } = \langle E_{\textit {dp}} \rangle _{\tau } + 1/6$. Consistent with the work by Hughes et al. (J. Fluid Mech., vol. 729, 2013) on three-dimensional Rayleigh–Bénard convection, we report analytical expressions for the energetics and efficiencies of HS-RBC in terms of the Rayleigh number and the global Nusselt number. Additionally, we performed numerical experiments to illustrate the application of the energetics for the analysis of HS-RBC. Finally, we discuss the impact of the thermal forcing and the geometrical control exerted by Hele-Shaw cells on the development of boundary layers, protoplumes and the self-organisation of large-scale flows.

JFM classification

Low-Reynolds-number flows: Hele-Shaw flows Flow Control: Mixing enhancement
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 930 , 10 January 2022 , A16
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlers, G., Funfschilling, D. & Bodenschatz, E. 2009 a Transitions in heat transport by turbulent convection at Rayleigh numbers up to 1015. New J. Phys. 11 (12), 123001.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 b Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Barkan, R., Winters, K. & Llewellyn Smith, S. 2013 Rotating horizontal convection. J. Fluid Mech. 723, 556–586.CrossRefGoogle Scholar
Caulfield, C.P. 2021 Layering, instabilities, and mixing in turbulent stratified flows. Annu. Rev. Fluid Mech. 53 (1), 113–145.CrossRefGoogle Scholar
Caulfield, C.-C.P. 2020 Open questions in turbulent stratified mixing: do we even know what we do not know? Phys. Rev. Fluids 5, 110518.CrossRefGoogle Scholar
Cooper, C.A., Crews, J.B., Schumer, R., Breitmeyer, R.J., Voepel, H. & Decker, D.L. 2014 Experimental investigation of transient thermal convection in porous media. Transp. Porous Media 104 (2), 335–347.CrossRefGoogle Scholar
Davies Wykes, M., Hughes, G. & Dalziel, S. 2015 On the meaning of mixing efficiency for buoyancy-driven mixing in stratified turbulent flows. J. Fluid Mech. 781, 261–275.CrossRefGoogle Scholar
De Paoli, M., Alipour, M. & Soldati, A. 2020 How non-darcy effects influence scaling laws in Hele-Shaw convection experiments. J. Fluid Mech. 892, A41.CrossRefGoogle Scholar
Dickson, M.H. & Fanelli, M. 2013 Geothermal Energy: Utilization and Technology, 1st edn. Routledge.CrossRefGoogle Scholar
Doering, C.R. & Constantin, P. 1998 Bounds for heat transport in a porous layer. J. Fluid Mech. 376, 263–296.CrossRefGoogle Scholar
Forget, G. & Ferreira, D. 2019 Global ocean heat transport dominated by heat export from the tropical pacific. Nat. Geosci. 12 (5), 351–354.CrossRefGoogle Scholar
Funfschilling, D., Bodenschatz, E. & Ahlers, G. 2009 Search for the ‘ultimate state’ in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 103, 014503.CrossRefGoogle Scholar
Gayen, B., Hughes, G.O. & Griffiths, R.W. 2013 Completing the mechanical energy pathways in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 111 (12), 124301.CrossRefGoogle ScholarPubMed
Grant, M.A. & Bixley, P.F. 2011 Geothermal Reservoirs. Elsevier.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23 (4), 045108.CrossRefGoogle Scholar
Hewitt, D.R. 2020 Vigorous convection in porous media. Proc. R. Soc. Lond. A 476 (2239), 20200111.Google ScholarPubMed
Hewitt, D.R., Neufeld, J.A. & Lister, J.R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108, 224503.CrossRefGoogle Scholar
Hidalgo, J.J., Fe, J., Cueto-Felgueroso, L. & Juanes, R. 2012 Scaling of convective mixing in porous media. Phys. Rev. Lett. 109 (26), 264503.CrossRefGoogle ScholarPubMed
Hughes, G., Gayen, B. & Griffiths, R. 2013 Available potential energy in Rayleigh–Bénard convection. J. Fluid Mech. 729, R3.CrossRefGoogle Scholar
Jha, B., Cueto-Felgueroso, L. & Juanes, R. 2011 Fluid mixing from viscous fingering. Phys. Rev. Lett. 106, 194502.CrossRefGoogle ScholarPubMed
Kimura, S., Schubert, G. & Straus, J.M. 1986 Route to chaos in porous-medium thermal convection. J. Fluid Mech. 166, 305–324.CrossRefGoogle Scholar
Korenaga, J. 2020 Plate tectonics and surface environment: role of the oceanic upper mantle. Earth-Sci. Rev. 205, 103185.CrossRefGoogle Scholar
Le Gall, A., et al. 2017 Thermally anomalous features in the subsurface of Enceladus's south polar terrain. Nat. Astron. 1 (4), 0063.CrossRefGoogle Scholar
Le Reun, T. & Hewitt, D.R. 2020 Internally heated porous convection: an idealized model for Enceladus’ hydrothermal activity. J. Geophys. Res.: Planet. 125 (7), e2020JE006451.CrossRefGoogle Scholar
Lele, S.K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.CrossRefGoogle Scholar
Letelier, J.A., Herrera, P., Mujica, N. & Ortega, J.H. 2016 Enhancement of synthetic Schlieren image resolution using total variation optical flow: application to thermal experiments in a Hele-Shaw cell. Exp. Fluids 57 (2), 18.CrossRefGoogle Scholar
Letelier, J.A., Mujica, N. & Ortega, J.H. 2019 Perturbative corrections for the scaling of heat transport in a Hele-Shaw geometry and its application to geological vertical fractures. J. Fluid Mech. 864, 746–767.CrossRefGoogle Scholar
Letelier, J.A., O'Sullivan, J., Reich, M., Veloso, E., Sánchez-Alfaro, P., Aravena, D., Muñoz, M. & Morata, D. 2021 Reservoir architecture model and heat transfer modes in the El Tatio-La Torta geothermal system, Central Andes of northern Chile. Geothermics 89, 101940.CrossRefGoogle Scholar
Murphy, H.D. 1979 Convective instabilities in vertical fractures and faults. J. Geophys. Res.: Solid Earth 84 (B11), 6121–6130.CrossRefGoogle Scholar
Nield, D.A. & Bejan, A. 2013 Convection in porous media. In Internal Natural Convection: Heating from Below, pp. 221–329. Springer.CrossRefGoogle Scholar
Otero, J., Dontcheva, L.A., Johnston, H., Worthing, R.A., Kurganov, A., Petrova, G. & Doering, C.R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.CrossRefGoogle Scholar
Paoli, M.D., Giurgiu, V., Zonta, F. & Soldati, A. 2019 Universal behavior of scalar dissipation rate in confined porous media. Phys. Rev. Fluids 4 (10), 101501.CrossRefGoogle Scholar
Peltier, W.R. & Caulfield, C.P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35 (1), 135–167.CrossRefGoogle Scholar
Pirozzoli, S., De Paoli, M., Zonta, F. & Soldati, A. 2021 Towards the ultimate regime in Rayleigh–Darcy convection. J. Fluid Mech. 911, R4.CrossRefGoogle Scholar
Sparks, W.B., Schmidt, B.E., McGrath, M.A., Hand, K.P., Spencer, J.R., Cracraft, M. & Deustua, S.E. 2017 Active cryovolcanism on Europa? Astrophys. J. Lett. 839 (2), L18.CrossRefGoogle Scholar
Tackley, P.J. 2000 Mantle convection and plate tectonics: toward an integrated physical and chemical theory. Science 288 (5473), 2002–2007.CrossRefGoogle ScholarPubMed
Togni, R., Cimarelli, A. & De Angelis, E. 2015 Physical and scale-by-scale analysis of Rayleigh–Bénard convection. J. Fluid Mech. 782, 380–404.CrossRefGoogle Scholar
Tournier, C., Genthon, P. & Rabinowicz, M. 2000 The onset of natural convection in vertical fault planes:consequences for the thermal regime in crystalline basementsand for heat recovery experiments. Geophys. J. Intl 140 (3), 500–508.CrossRefGoogle Scholar
Ulloa, H.N., Winters, K.B., Wüest, A. & Bouffard, D. 2019 Differential heating drives downslope flows that accelerate mixed-layer warming in ice-covered waters. Geophys. Res. Lett. 46, 13872–13882.CrossRefGoogle Scholar
Vallis, G.K. 2017 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Winters, K., Lombard, P., Riley, J. & D'Asaro, E. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.CrossRefGoogle Scholar
Winters, K.B. & Barkan, R. 2013 Available potential energy density for Boussinesq fluid flow. J. Fluid Mech. 714, 476–488.CrossRefGoogle Scholar
Winters, K.B. & D'Asaro, E.A. 1996 Diascalar flux and the rate of fluid mixing. J. Fluid Mech. 317, 179–193.CrossRefGoogle Scholar
Winters, K.B. & de la Fuente, A. 2012 Modelling rotating stratified flows at laboratory-scale using spectrally-based DNS. Ocean Model. 49–50, 47–59.CrossRefGoogle Scholar
Winters, K.B., Ulloa, H.N., Wüest, A. & Bouffard, D. 2019 Energetics of radiatively heated ice-covered lakes. Geophys. Res. Lett. 46 (15), 8913–8925.CrossRefGoogle Scholar
Zilitinkevich, S.S., Elperin, T., Kleeorin, N. & Rogachevskii, I. 2007 Energy- and flux-budget (EFB) turbulence closure model for stably stratified flows. Part I: steady-state, homogeneous regimes. Boundary-Layer Meteorol. 125 (2), 167–191.CrossRefGoogle Scholar