Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-27T05:37:13.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Electric-field-controlled diffusion of anisotropic particles: theory and experiment

Published online by Cambridge University Press:  17 August 2021

Tianyu Yuan ,
Wuhan Yuan ,
Liping Liu  and
Jerry W. Shan
Tianyu Yuan
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, PR China Department of Mechanical and Aerospace Engineering, Rutgers University, Piscataway, NJ 08854, USA
Wuhan Yuan*
Affiliation:
Department of Mechanical and Aerospace Engineering, Rutgers University, Piscataway, NJ 08854, USA
Liping Liu
Affiliation:
Department of Mechanical and Aerospace Engineering, Rutgers University, Piscataway, NJ 08854, USA Department of Mathematics, Rutgers University, Piscataway, NJ 08854, USA
Jerry W. Shan
Affiliation:
Department of Mechanical and Aerospace Engineering, Rutgers University, Piscataway, NJ 08854, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

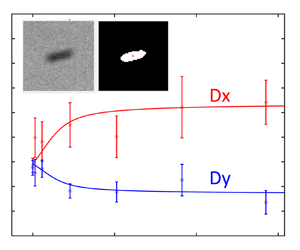
We report on a theoretical and experimental study on the anisotropic diffusion of isolated prolate spheroidal particles in the presence of an aligning potential field. By analysing the microscopic stochastic equations of motion, we obtained the coarse-grained Fokker–Planck equations that govern the evolution of the probability distributions of particle orientation in various configurational spaces. In particular, we found explicit formulae for the diffusion coefficients parallel ($D_x$) and perpendicular ($D_y$) to the field direction in the long-time limit. The predicted results were experimentally validated by measuring the Brownian motions of fluid-suspended carbon nanotubes in an electric field. Good agreement was observed between theoretical and experimental results, both of which showed increasing $D_x$ and decreasing $D_y$ with increasing field strength up to a critical field strength beyond which both curves start to flatten. Our theory and experimental results provide a framework for understanding the coupling between rotation and translation in a diffusion process, and for controlling the diffusion of particles with aligning potential fields.

JFM classification

Complex Fluids: Suspensions Mathematical Foundations: General fluid mechanics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 924 , 10 October 2021 , A42
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aristov, M., Eichhorn, R. & Bechinger, C. 2013 Separation of chiral colloidal particles in a helical flow field. Soft Matt. 9 (8), 2525–2530.CrossRefGoogle Scholar
Aurell, E., Bo, S., Dias, M., Eichhorn, R. & Marino, R. 2016 Diffusion of a Brownian ellipsoid in a force field. Europhys. Lett. 114 (3), 30005.CrossRefGoogle Scholar
Bernal, J.M.G. & De La Torre, J.G. 1980 Transport properties and hydrodynamic centers of rigid macromolecules with arbitrary shapes. Biopolymers 19 (4), 751–766.CrossRefGoogle Scholar
Brenner, H. 1965 Coupling between the translational and rotational Brownian motions of rigid particles of arbitrary shape I. Helicoidally isotropic particles. J. Colloid Sci. 20 (2), 104–122.CrossRefGoogle Scholar
Brenner, H. 1967 Coupling between the translational and rotational Brownian motions of rigid particles of arbitrary shape: II. General theory. J. Colloid Interface Sci. 23 (3), 407–436.CrossRefGoogle Scholar
Castellano, R.J., Akin, C., Giraldo, G., Kim, S., Fornasiero, F. & Shan, J.W. 2015 Electrokinetics of scalable, electric-field-assisted fabrication of vertically aligned carbon-nanotube/polymer composites. J. Appl. Phys. 117 (21), 214306.CrossRefGoogle Scholar
Castellano, R.J., Praino, R.F., Meshot, E.R., Chen, C., Fornasiero, F. & Shan, J.W. 2020 Scalable electric-field-assisted fabrication of vertically aligned carbon nanotube membranes with flow enhancement. Carbon 157, 208–216.CrossRefGoogle Scholar
Cetindag, S., Tiwari, B., Zhang, D., Yap, Y.K., Kim, S. & Shan, J.W. 2017 Surface-charge effects on the electro-orientation of insulating boron-nitride nanotubes in aqueous suspension. J. Colloid Interface Sci. 505, 1185–1192.CrossRefGoogle ScholarPubMed
Chakrabarty, A., Konya, A., Wang, F., Selinger, J.V., Sun, K. & Wei, Q.H. 2014 Brownian motion of arbitrarily shaped particles in two dimensions. Langmuir 30 (46), 13844–13853.CrossRefGoogle ScholarPubMed
Cheong, F.C. & Grier, D.G. 2010 Rotational and translational diffusion of copper oxide nanorods measured with holographic video microscopy. Opt. Express 18 (7), 6555–6562.CrossRefGoogle ScholarPubMed
Doi, M. & Makino, M. 2005 Sedimentation of particles of general shape. Phys. Fluids 17 (4), 043601.CrossRefGoogle Scholar
Einstein, A. 1905 On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat. Ann. Phys. (Berlin) 17, 549–560.CrossRefGoogle Scholar
Evans, L.C. 2012 An Introduction to Stochastic Differential Equations. American Mathematical Society.Google Scholar
Grima, R. & Yaliraki, S.N. 2007 Brownian motion of an asymmetrical particle in a potential field. J. Chem. Phys. 127 (8), 084511.CrossRefGoogle Scholar
Güell, O., Tierno, P. & Sagués, F. 2010 Anisotropic diffusion of a magnetically torqued ellipsoidal microparticle. Eur. Phys. J. Spec. Top. 187 (1), 15–20.CrossRefGoogle Scholar
Guo, X., Su, J. & Guo, H. 2012 Electric field induced orientation and self-assembly of carbon nanotubes in water. Soft Matt. 8 (4), 1010–1016.CrossRefGoogle Scholar
Han, Y., Alsayed, A., Nobili, M. & Yodh, A.G. 2009 Quasi-two-dimensional diffusion of single ellipsoids: aspect ratio and confinement effects. Phys. Rev. E 80 (1), 011403.CrossRefGoogle ScholarPubMed
Han, Y., Alsayed, A.M., Nobili, M., Zhang, J., Lubensky, T.C. & Yodh, A.G. 2006 Brownian motion of an ellipsoid. Science 314 (5799), 626–630.CrossRefGoogle ScholarPubMed
Jones, T.B. 1995 Chapter 5 – orientation of nonspherical particles. In Electromechanics of Particles (ed. T.B. Jones), pp. 110–138. Cambridge University Press.CrossRefGoogle Scholar
Kim, S. & Karrila, S. 1991 Chapter 3 – the disturbance field of a single particle in a steady flow. In Microhydrodynamics (ed. S. Kim & S.J. Karrila), pp. 47–81. Butterworth-Heinemann.CrossRefGoogle Scholar
Köster, S., Steinhauser, D. & Pfohl, T. 2005 Brownian motion of actin filaments in confining microchannels. J. Phys. Condens. Matter 17 (49), S4091–S4104.CrossRefGoogle Scholar
Kubo, R. 1966 The fluctuation-dissipation theorem. Rep. Prog. Phys. 29 (1), 255–284.CrossRefGoogle Scholar
Makino, M. & Doi, M. 2003 Sedimentation of a particle with translation-rotation coupling. J. Phys. Soc. Japan 72 (11), 2699–2701.CrossRefGoogle Scholar
Maragó, O.M., et al. 2010 Brownian motion of graphene. ACS Nano 4 (12), 7515–7523.CrossRefGoogle ScholarPubMed
Michalet, X. 2010 Mean square displacement analysis of single-particle trajectories with localization error: Brownian motion in an isotropic medium. Phys. Rev. E 82 (4), 041914.CrossRefGoogle Scholar
Mijalkov, M. & Volpe, G. 2013 Sorting of chiral microswimmers. Soft Matt. 9 (28), 6376–6381.CrossRefGoogle Scholar
Obasanjo, C.A. 2016 The response of an ellipsoidal colloid particle in an ac field. Master's thesis, Ahmadu Bello University.Google Scholar
Perrin, F. 1934 Mouvement brownien d'un ellipsoide-I. Dispersion diélectrique pour des molécules ellipsoidales. J. Phys. Radium 5, 497–511.CrossRefGoogle Scholar
Perrin, F. 1936 Mouvement brownien d'un ellipsoide (ii). Rotation libre et dépolarisation des fluorescences. Translation et diffusion de molécules ellipsoidales. J. Phys. Radium 7 (1), 1–11.CrossRefGoogle Scholar
Perrin, J. 1909 Le mouvement brownien et la réalité moleculaire. Ann. Chim. Phys. 18 (8), 5–114.Google Scholar
Segovia-Gutiérrez, J.P., Escobedo-Sánchez, M.A., Sarmiento-Gómez, E. & Egelhaaf, S.U. 2019 Diffusion of anisotropic particles in random energy landscapes-an experimental study. Front. Phys. 7, 224.CrossRefGoogle Scholar
Squires, T.M. & Bazant, M.Z. 2006 Breaking symmetries in induced-charge electro-osmosis and electrophoresis. J. Fluid Mech. 560, 65–101.CrossRefGoogle Scholar
Van Kampen, N.G. 2007 Chapter viii – the fokker–planck equation. In Stochastic Processes in Physics and Chemistry (Third Edition), Third edition edn. (ed. N.G. Van Kampen), pp. 193–218. Elsevier.CrossRefGoogle Scholar
Wang, A., Dimiduk, T.G., Fung, J., Razavi, S., Kretzschmar, I., Chaudhary, K. & Manoharan, V.N. 2014 Using the discrete dipole approximation and holographic microscopy to measure rotational dynamics of non-spherical colloidal particles. J. Quant. Spectrosc. Radiat. Transfer 146, 499–509.CrossRefGoogle Scholar
Yuan, W., Liu, L. & Shan, J.W. 2017 Tunable acoustic attenuation in dilute suspensions of subwavelength, non-spherical magnetic particles. J. Appl. Phys. 121 (4), 045110.CrossRefGoogle Scholar
Yuan, W., Tutuncuoglu, G., Mohabir, A., Liu, L., Feldman, L.C., Filler, M.A. & Shan, J.W. 2019 Contactless electrical and structuralcharacterization of semiconductor nanowires with axially modulated doping profiles. Small 15 (15), 1805140.CrossRefGoogle ScholarPubMed
Supplementary material: File

Yuan et al. supplementary material

Yuan et al. supplementary material

Download Yuan et al. supplementary material(File)
File 501 KB