Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Olsthoorn, Jason
and
Dalziel, Stuart B.
2015.
Vortex-ring-induced stratified mixing.
Journal of Fluid Mechanics,
Vol. 781,
Issue. ,
p.
113.
Hogg, Charlie A. R.
Dalziel, Stuart B.
Huppert, Herbert E.
and
Imberger, Jörg
2015.
Inclined gravity currents filling basins: The influence of Reynolds number on entrainment into gravity currents.
Physics of Fluids,
Vol. 27,
Issue. 9,
Chalamalla, Vamsi K.
and
Sarkar, Sutanu
2015.
Mixing, Dissipation Rate, and Their Overturn-Based Estimates in a Near-Bottom Turbulent Flow Driven by Internal Tides.
Journal of Physical Oceanography,
Vol. 45,
Issue. 8,
p.
1969.
Jiao, Yang
and
Dewar, W. K.
2015.
The Energetics of Centrifugal Instability.
Journal of Physical Oceanography,
Vol. 45,
Issue. 6,
p.
1554.
Davies Wykes, Megan S.
Hughes, Graham O.
and
Dalziel, Stuart B.
2015.
On the meaning of mixing efficiency for buoyancy-driven mixing in stratified turbulent flows.
Journal of Fluid Mechanics,
Vol. 781,
Issue. ,
p.
261.
Dossmann, Yvan
G. Rosevear, Madelaine
Griffiths, Ross W.
McC. Hogg, Andrew
Hughes, Graham O.
and
Copeland, Michael
2016.
Experiments with mixing in stratified flow over a topographic ridge.
Journal of Geophysical Research: Oceans,
Vol. 121,
Issue. 9,
p.
6961.
Venaille, A.
Gostiaux, L.
and
Sommeria, J.
2017.
A statistical mechanics approach to mixing in stratified fluids.
Journal of Fluid Mechanics,
Vol. 810,
Issue. ,
p.
554.
Carminati, Marco
and
Luzzatto-Fegiz, Paolo
2017.
Conduino: Affordable and high-resolution multichannel water conductivity sensor using micro USB connectors.
Sensors and Actuators B: Chemical,
Vol. 251,
Issue. ,
p.
1034.
Williams, R. J. R.
2017.
Rayleigh–Taylor mixing between density stratified layers.
Journal of Fluid Mechanics,
Vol. 810,
Issue. ,
p.
584.
Zhou, Ye
2017.
Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II.
Physics Reports,
Vol. 723-725,
Issue. ,
p.
1.
Rao, P.
Caulfield, C. P.
and
Gibbon, J. D.
2017.
Nonlinear effects in buoyancy-driven variable-density turbulence.
Journal of Fluid Mechanics,
Vol. 810,
Issue. ,
p.
362.
Dossmann, Yvan
Pollet, Florence
Odier, Philippe
and
Dauxois, Thierry
2017.
Mixing and Formation of Layers by Internal Wave Forcing.
Journal of Geophysical Research: Oceans,
Vol. 122,
Issue. 12,
p.
9906.
Sohail, Taimoor
Gayen, Bishakhdatta
and
Hogg, Andrew McC.
2018.
Convection Enhances Mixing in the Southern Ocean.
Geophysical Research Letters,
Vol. 45,
Issue. 9,
p.
4198.
Thorpe, S. A.
2018.
Models of energy loss from internal waves breaking in the ocean.
Journal of Fluid Mechanics,
Vol. 836,
Issue. ,
p.
72.
Aljahdaly, Noufe H.
and
Hadji, Layachi
2018.
Buoyancy-Driven Rayleigh–Taylor Instability in a Vertical Channel.
Journal of Non-Equilibrium Thermodynamics,
Vol. 43,
Issue. 4,
p.
289.
Ulloa, Hugo N.
Wüest, Alfred
and
Bouffard, Damien
2018.
Mechanical energy budget and mixing efficiency for a radiatively heated ice-covered waterbody.
Journal of Fluid Mechanics,
Vol. 852,
Issue. ,
Al Assaad, Douaa
Ghali, Kamel
and
Ghaddar, Nesreen
2018.
Effectiveness of intermittent personalized ventilation assisting a chilled ceiling for enhanced thermal comfort and acceptable indoor air quality.
Building and Environment,
Vol. 144,
Issue. ,
p.
9.
Monismith, Stephen G.
Koseff, Jeffrey R.
and
White, Brian L.
2018.
Mixing Efficiency in the Presence of Stratification: When Is It Constant?.
Geophysical Research Letters,
Vol. 45,
Issue. 11,
p.
5627.
Wieland, Scott A.
Hamlington, Peter E.
Reckinger, Scott J.
and
Livescu, Daniel
2019.
Effects of isothermal stratification strength on vorticity dynamics for single-mode compressible Rayleigh-Taylor instability.
Physical Review Fluids,
Vol. 4,
Issue. 9,
Puthan, Pranav
Jalali, Masoud
Chalamalla, Vamsi K.
and
Sarkar, Sutanu
2019.
Energetics and mixing in buoyancy-driven near-bottom stratified flow.
Journal of Fluid Mechanics,
Vol. 869,
Issue. ,
p.
214.
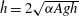 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\dot{h} = 2 \sqrt{\alpha A g h}$ (where
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\dot{h} = 2 \sqrt{\alpha A g h}$ (where 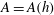 $A = A(h)$ is the Atwood number across the mixing region when it extends a height
$A = A(h)$ is the Atwood number across the mixing region when it extends a height 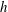 $h$,
$h$,  $g$ is acceleration due to gravity and
$g$ is acceleration due to gravity and  $\alpha $ is a constant). This model shows good agreement with experiments when the value of the constant
$\alpha $ is a constant). This model shows good agreement with experiments when the value of the constant  $\alpha $ is set to 0.07, the value found in experiments of RTI between two homogeneous layers (where the height of the turbulent mixing region increases as
$\alpha $ is set to 0.07, the value found in experiments of RTI between two homogeneous layers (where the height of the turbulent mixing region increases as 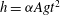 $h =\alpha A g t^2$, an expression which is equivalent to that derived for
$h =\alpha A g t^2$, an expression which is equivalent to that derived for 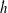 $\dot{h}$).
$\dot{h}$).

