Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T04:44:53.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of radius ratio on annular centrifugal Rayleigh–Bénard convection

Published online by Cambridge University Press:  10 November 2021

Dongpu Wang Open the ORCID record for Dongpu Wang [Opens in a new window] ,
Hechuan Jiang Open the ORCID record for Hechuan Jiang [Opens in a new window] ,
Shuang Liu Open the ORCID record for Shuang Liu [Opens in a new window] ,
Xiaojue Zhu Open the ORCID record for Xiaojue Zhu [Opens in a new window]  and
Chao Sun Open the ORCID record for Chao Sun [Opens in a new window]
Dongpu Wang
Affiliation:
Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of MoE, and Department of Thermal Engineering, Tsinghua University, Beijing 100084, PR China
Hechuan Jiang*
Affiliation:
Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of MoE, and Department of Thermal Engineering, Tsinghua University, Beijing 100084, PR China Huaneng Clean Energy Research Institute, Beijing 102209, PR China
Shuang Liu
Affiliation:
Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of MoE, and Department of Thermal Engineering, Tsinghua University, Beijing 100084, PR China Yau Mathematical Sciences Center, Tsinghua University, Beijing 100084, PR China
Xiaojue Zhu
Affiliation:
Max Planck Institute for Solar System Research, Justus-von-Liebig-Weg 3, Göttingen 37077, Germany
Chao Sun*
Affiliation:
Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of MoE, and Department of Thermal Engineering, Tsinghua University, Beijing 100084, PR China Department of Engineering Mechanics, School of Aerospace Engineering, Tsinghua University, Beijing 100084, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

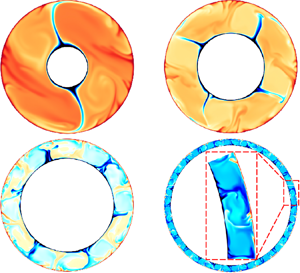
We report on a three-dimensional direct numerical simulation study of flow structure and heat transport in the annular centrifugal Rayleigh–Bénard convection (ACRBC) system, with cold inner and hot outer cylinders corotating axially, for the Rayleigh number range $Ra \in [{10^6},{10^8}]$ and radius ratio range $\eta = {R_i}/{R_o} \in [0.3,0.9]$ ($R_i$ and $R_o$ are the radius of the inner and outer cylinders, respectively). This study focuses on the dependence of flow dynamics, heat transport and asymmetric mean temperature fields on the radius ratio $\eta$. For the inverse Rossby number $Ro^{-1} = 1$, as the Coriolis force balances inertial force, the flow is in the inertial regime. The mechanisms of zonal flow revolving in the prograde direction in this regime are attributed to the asymmetric movements of plumes and the different curvatures of the cylinders. The number of roll pairs is smaller than the circular roll hypothesis as the convection rolls are probably elongated by zonal flow. The physical mechanism of zonal flow is verified by the dependence of the drift frequency of the large-scale circulation (LSC) rolls and the space- and time-averaged azimuthal velocity on $\eta$. The larger $\eta$ is, the weaker the zonal flow becomes. We show that the heat transport efficiency increases with $\eta$. It is also found that the bulk temperature deviates from the arithmetic mean temperature and the deviation increases as $\eta$ decreases. This effect can be explained by a simple model that accounts for the curvature effects and the radially dependent centrifugal force in ACRBC.

JFM classification

Turbulent Flows: Turbulent convection Turbulent Flows: Turbulence simulation Turbulent Flows: Rotating turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 930 , 10 January 2022 , A19
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Azouni, M.A., Bolton, E.W. & Busse, F.H. 1985 Convection driven by centrifugal bouyancy in a rotating annulus. Geophys. Astrophys. Fluid Dyn. 34 (1–4), 301–317.CrossRefGoogle Scholar
Blass, A., Zhu, X., Verzicco, R., Lohse, D. & Stevens, R.J.A.M. 2020 Flow organization and heat transfer in turbulent wall sheared thermal convection. J. Fluid Mech. 897, A22.CrossRefGoogle ScholarPubMed
Bohn, D., Deuker, E., Emunds, R. & Gorzelitz, V. 1995 Experimental and theoretical investigations of heat transfer in closed gas-filled rotating annuli. Trans. ASME J. Turbomach. 117 (1), 175–183.CrossRefGoogle Scholar
Busse, F.H. 1994 Convection driven zonal flows and vortices in the major planets. Chaos 4 (2), 123–134.CrossRefGoogle ScholarPubMed
Busse, F.H. & Carrigan, C.R. 1974 Convection induced by centrifugal buoyancy. J. Fluid Mech. 62 (3), 579–592.CrossRefGoogle Scholar
Busse, F.H. & Or, A.C. 1986 Convection in a rotating cylindrical annulus: thermal Rossby waves. J. Fluid Mech. 166, 173–187.CrossRefGoogle Scholar
Cardin, P. & Olson, P. 1994 Chaotic thermal convection in a rapidly rotating spherical shell: consequences for flow in the outer core. Phys. Earth Planet. Inter. 82 (3), 235–259.CrossRefGoogle Scholar
Chalghoum, I., Elaoud, S., Kanfoudi, H. & Akrout, M. 2018 The effects of the rotor-stator interaction on unsteady pressure pulsation and radial force in a centrifugal pump. J. Hydrodyn. 30 (4), 672–681.CrossRefGoogle Scholar
Chen, X., Wang, D.-P. & Xi, H.-D. 2020 Reduced flow reversals in turbulent convection in the absence of corner vortices. J. Fluid Mech. 891, R5.CrossRefGoogle Scholar
Cheng, L., Abraham, J., Hausfather, Z. & Trenberth, K.E. 2019 How fast are the oceans warming? Science 363, 128–129.CrossRefGoogle ScholarPubMed
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 1–25.CrossRefGoogle ScholarPubMed
Chong, K.L., Yang, Y., Huang, S.-D., Zhong, J.-Q., Stevens, R.J.A.M., Verzicco, R., Lohse, D. & Xia, K.-Q. 2017 Confined Rayleigh–Bénard, rotating Rayleigh–Bénard, and double diffusive convection: a unifying view on turbulent transport enhancement through coherent structure manipulation. Phys. Rev. Lett. 119, 064501.CrossRefGoogle ScholarPubMed
Courant, R., Friedrichs, K. & Lewy, H. 1928 Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 100, 32–74.CrossRefGoogle Scholar
Cushman-Roisin, B. & Beckers, J.-M. 2011 The coriolis force. In Introduction to Geophysical Fluid Dynamics, chap. 2, pp. 42–45. Academic Press.CrossRefGoogle Scholar
Fowlis, W.W. & Hide, R. 1965 Thermal convection in a rotating annulus of liquid: effect of viscosity on the transition between axisymmetric and non-axisymmetric flow regimes. J. Atmos. Sci. 22, 541–558.Google Scholar
Gastine, T., Wicht, J. & Aurnou, J.M. 2015 Turbulent Rayleigh–Bénard convection in spherical shells. J. Fluid Mech. 778, 721–764.CrossRefGoogle Scholar
Goluskin, D., Johnston, H., Flierl, G.R. & Spiegel, E.A. 2014 Convectively driven shear and decreased heat flux. J. Fluid Mech. 759, 360–385.CrossRefGoogle Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High–Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48 (1), 53–80.CrossRefGoogle Scholar
von Hardenberg, J., Goluskin, D., Provenzale, A. & Spiegel, E.A. 2015 Generation of large-scale winds in horizontally anisotropic convection. Phys. Rev. Lett. 115, 134501.CrossRefGoogle ScholarPubMed
Hartmann, D.L., Moy, L.A. & Fu, Q. 2001 Tropical convection and the energy balance at the top of the atmosphere. J. Clim. 14 (24), 4495.2.0.CO;2>CrossRefGoogle Scholar
Heimpel, M., Aurnou, J. & Wicht, J. 2005 Simulation of equatorial and high-latitude jets on Jupiter in a deep convection model. Nature 438, 193–196.CrossRefGoogle Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement-induced heat-transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111, 104501.CrossRefGoogle ScholarPubMed
Huang, S.-D. & Xia, K.-Q. 2016 Effects of geometric confinement in quasi-2-D turbulent Rayleigh–Bénard convection. J. Fluid Mech. 794, 639–654.CrossRefGoogle Scholar
Jiang, H., Zhu, X., Mathai, V., Verzicco, R., Lohse, D. & Sun, C. 2018 Controlling heat transport and flow structures in thermal turbulence using ratchet surfaces. Phys. Rev. Lett. 120, 044501.CrossRefGoogle ScholarPubMed
Jiang, H., Zhu, X., Wang, D., Huisman, S.G. & Sun, C. 2020 Supergravitational turbulent thermal convection. Sci. Adv. 6, eabb8676.CrossRefGoogle ScholarPubMed
Kang, C., Meyer, A., Yoshikawa, H.N. & Mutabazi, I. 2019 Numerical study of thermal convection induced by centrifugal buoyancy in a rotating cylindrical annulus. Phys. Rev. Fluids 4, 043501.CrossRefGoogle Scholar
King, M.P., Wilson, M. & Owen, J.M. 2005 Rayleigh–Bénard convection in open and closed rotating cavities. Trans. ASME J. Engng Gas Turbines Power 129 (2), 305–311.CrossRefGoogle Scholar
Kunnen, R.P.J., Ostilla-Mónico, R., van der Poel, E.P., Verzicco, R. & Lohse, D. 2016 Transition to geostrophic convection: the role of the boundary conditions. J. Fluid Mech. 799, 413–432.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42 (1), 335–364.CrossRefGoogle Scholar
Mckenzie, D.P., Roberts, J.M. & Weiss, N.O. 1974 Convection in the earth's mantle: towards a numerical simulation. J. Fluid Mech. 62 (3), 465–538.CrossRefGoogle Scholar
Michael Owen, J. & Long, C.A. 2015 Review of buoyancy-induced flow in rotating cavities. Trans. ASME J. Turbomach. 137 (11), 111001.CrossRefGoogle Scholar
Oberbeck, A. 1879 Ueber die Wärmeleitung der Flüssigkeiten bei Berücksichtigung der Strömungen infolge von Temperaturdifferenzen. Ann. Phys. 243 (6), 271–292.CrossRefGoogle Scholar
Ostilla, R., Stevens, R.J.A.M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.CrossRefGoogle Scholar
Pitz, D.B., Chew, J.W., Marxen, O. & Hills, N.J. 2017 a Direct numerical simulation of rotating cavity flows using a spectral element-Fourier method. Trans. ASME J. Engng Gas Turbines Power 139 (7), 072602.CrossRefGoogle Scholar
Pitz, D.B., Marxen, O. & Chew, J.W. 2017 b Onset of convection induced by centrifugal buoyancy in a rotating cavity. J. Fluid Mech. 826, 484–502.CrossRefGoogle Scholar
van der Poel, E.P., Ostilla-Mónico, R., Donners, J. & Verzicco, R. 2015 a A pencil distributed finite difference code for strongly turbulent wall-bounded flows. Comput. Fluids 116, 10–16.CrossRefGoogle Scholar
van der Poel, E.P., Stevens, R.J.A.M. & Lohse, D. 2011 Connecting flow structures and heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. E 84, 045303.CrossRefGoogle ScholarPubMed
van der Poel, E.P., Verzicco, R., Grossmann, S. & Lohse, D. 2015 b Plume emission statistics in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 772, 5–15.CrossRefGoogle Scholar
Porco, C.C., et al. 2003 Cassini imaging of Jupiter's atmosphere, satellites, and rings. Science 299, 1541–1547.CrossRefGoogle ScholarPubMed
Read, P.L., Morice-Atkinson, X., Allen, E.J. & Castrejón-Pita, A.A. 2017 Phase synchronization of baroclinic waves in a differentially heated rotating annulus experiment subject to periodic forcing with a variable duty cycle. Chaos 27 (12), 127001.CrossRefGoogle Scholar
Read, P.L. & Risch, S.H. 2011 A laboratory study of global-scale wave interactions in baroclinic flow with topography I: multiple flow regimes. Geophys. Astrophys. Fluid Dyn. 105 (2–3), 128–160.CrossRefGoogle Scholar
Rhines, P.B. 1975 Waves and turbulence on a beta-plane. J. Fluid Mech. 69 (3), 417–443.CrossRefGoogle Scholar
Rouhi, A., Lohse, D., Marusic, I., Sun, C. & Chung, D. 2021 Coriolis effect on centrifugal buoyancy-driven convection in a thin cylindrical shell. J. Fluid Mech. 910, A32.CrossRefGoogle Scholar
Silano, G., Sreenivasan, K.R. & Verzicco, R. 2010 Numerical simulations of Rayleigh–Bénard convection for Prandtl numbers between $10^{- 1}$ and $10^4$ and Rayleigh numbers between $10^5$ and $10^9$. J. Fluid Mech. 662, 409–446.CrossRefGoogle Scholar
Sun, C., Ren, L.-Y., Song, H. & Xia, K.-Q. 2005 Heat transport by turbulent Rayleigh–Bénard convection in 1 m diameter cylindrical cells of widely varying aspect ratio. J. Fluid Mech. 542, 165–174.CrossRefGoogle Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123, 402–414.CrossRefGoogle Scholar
Wang, C., Jiang, L., Jiang, H., Sun, C. & Liu, S. 2021 Heat transfer and flow structure of two-dimensional thermal convection over ratchet surfaces. J. Hydrodyn. 33 (5), 93–103.CrossRefGoogle Scholar
Wang, Q., Chong, K.L., Stevens, R.J.A.M., Verzicco, R. & Lohse, D. 2020 From zonal flow to convection rolls in Rayleigh–Bénard convection with free-slip plates. J. Fluid Mech. 905, A21.CrossRefGoogle Scholar
Williams, G.P. 1971 Baroclinic annulus waves. J. Fluid Mech. 49 (3), 417–449.CrossRefGoogle Scholar
Wu, X.-Z. & Libchaber, A. 1991 Non-Boussinesq effects in free thermal convection. Phys. Rev. A 43, 2833–2839.CrossRefGoogle ScholarPubMed
Wyngaard, J.C. 1992 Atmospheric turbulence. Annu. Rev. Fluid Mech. 24 (1), 205–234.CrossRefGoogle Scholar
Xia, K.-Q. 2013 Current trends and future directions in turbulent thermal convection. Theor. Appl. Mech. Lett. 3 (5), 052001.CrossRefGoogle Scholar
Yano, J.-I., Talagrand, O. & Drossart, P. 2005 Deep two-dimensional turbulence: an idealized model for atmospheric jets of the giant outer planets. Geophys. Astrophys. Fluid Dyn. 99 (2), 137–150.CrossRefGoogle Scholar
Yik, H., Valori, V. & Weiss, S. 2020 Turbulent Rayleigh–Bénard convection under strong non-Oberbeck-Boussinesq conditions. Phys. Rev. Fluids 5, 103502.CrossRefGoogle Scholar
Yu, Y., Liu, F., Zhou, T., Gao, C. & Liu, Y. 2019 Numerical solutions of 2-D steady compressible natural convection using high-order flux reconstruction. Acta Mechanica Sin. 35, 401–410.CrossRefGoogle Scholar
Zhang, J., Childress, S. & Libchaber, A. 1997 Non-Boussinesq effect: thermal convection with broken symmetry. Phys. Fluids 9 (4), 1034–1042.CrossRefGoogle Scholar
Zhang, Y., Zhou, Q. & Sun, C. 2017 Statistics of kinetic and thermal energy dissipation rates in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 814, 165–184.CrossRefGoogle Scholar
Zhu, X., et al. 2018 AFiD-GPU: a versatile Navier–Stokes solver for wall-bounded turbulent flows on GPU clusters. Comput. Phys. Commun. 229, 199–210.CrossRefGoogle Scholar
Zou, H.-Y., Zhou, W.-F., Chen, X., Bao, Y., Chen, J. & She, Z.-S. 2019 Boundary layer structure in turbulent Rayleigh–Bénard convection in a slim box. Acta Mechanica Sin. 35, 713–728.CrossRefGoogle Scholar

Wang et al. supplementary movie 1

The movie shows the time series (total 100t) of the temperature fields on a \phi-r-plane for radius ratio η = 0.3 at Ra = 10^7

Download Wang et al. supplementary movie 1(Video)
Video 7.6 MB

Wang et al. supplementary movie 2

The movie shows the time series (total 100t) of the temperature fields on a \phi-r-plane for radius ratio η = 0.6 at Ra = 10^7

Download Wang et al. supplementary movie 2(Video)
Video 9.7 MB

Wang et al supplementary movie 3

The movie shows the time series (total 100t) of the temperature fields on a \phi-r-plane for radius ratio η = 0.9 at Ra = 10^7
Download Wang et al supplementary movie 3(Video)
Video 7.6 MB