Published online by Cambridge University Press: 12 November 2018
Experiments have shown that micron-sized distributed surface roughness can significantly promote transition in a three-dimensional boundary layer dominated by crossflow instability. This sensitive effect has not yet been fully explained physically and mathematically. Past studies focused on surface roughness exciting crossflow vortices and/or changing the local stability characteristics. The present paper seeks possible additional mechanisms by investigating the effects of distributed surface roughness on crossflow instability through resonant interactions with eigenmodes. A key observation is that the perturbation induced by roughness with specific wavenumbers can interact with two eigenmodes (travelling and stationary vortices) through triadic resonance, or interact with one eigenmode (stationary vortices) through Bragg scattering. Unlike the usual triadic resonance of neutral, or nearly neutral, eigenmodes, the present triadic resonance can take place among modes with 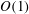 $O(1)$ growth rates, provided that these are equal; unlike the usual Bragg scattering involving neutral waves, crossflow stationary vortices can also be unstable. For these amplifying waves, the generalized triadic resonance and Bragg scattering are put forward, and the resulting corrections to the growth rates are derived by a multiple-scale method. The analysis is extended to the case where up to four crossflow vortices interact with each other in the presence of suitable roughness components. The numerical results for Falkner–Skan–Cooke boundary layers show that roughness with a small height (a few percent of the local boundary-layer thickness) can change growth rates substantially (by a more-or-less
$O(1)$ growth rates, provided that these are equal; unlike the usual Bragg scattering involving neutral waves, crossflow stationary vortices can also be unstable. For these amplifying waves, the generalized triadic resonance and Bragg scattering are put forward, and the resulting corrections to the growth rates are derived by a multiple-scale method. The analysis is extended to the case where up to four crossflow vortices interact with each other in the presence of suitable roughness components. The numerical results for Falkner–Skan–Cooke boundary layers show that roughness with a small height (a few percent of the local boundary-layer thickness) can change growth rates substantially (by a more-or-less 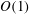 $O(1)$ amount). This sensitive effect is attributed to two facts: (i) the resonant nature of the triadic interaction and Bragg scattering, which makes the correction to the growth rate proportional to the roughness height, and (ii) the wavenumbers of the roughness component required for the resonance are close to those of the neutral stationary crossflow modes, as a result of which a small roughness can generate a large response. Another important effect of roughness is that its presence renders the participating eigenmodes, which are otherwise independent, fully coupled. Our theoretical results suggest that micron-sized distributed surface roughness influences significantly both the amplification and spectral composition of crossflow vortices.
$O(1)$ amount). This sensitive effect is attributed to two facts: (i) the resonant nature of the triadic interaction and Bragg scattering, which makes the correction to the growth rate proportional to the roughness height, and (ii) the wavenumbers of the roughness component required for the resonance are close to those of the neutral stationary crossflow modes, as a result of which a small roughness can generate a large response. Another important effect of roughness is that its presence renders the participating eigenmodes, which are otherwise independent, fully coupled. Our theoretical results suggest that micron-sized distributed surface roughness influences significantly both the amplification and spectral composition of crossflow vortices.