Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T14:22:26.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of wall suction on rotating disk absolute instability

Published online by Cambridge University Press:  24 February 2016

Joanna Ho ,
Thomas C. Corke  and
Eric Matlis
Joanna Ho
Affiliation:
University of Notre Dame, Institute for Flow Physics and Control, Aerospace and Mechanical Engineering Department, Notre Dame, IN 46556, USA
Thomas C. Corke*
Affiliation:
University of Notre Dame, Institute for Flow Physics and Control, Aerospace and Mechanical Engineering Department, Notre Dame, IN 46556, USA
Eric Matlis
Affiliation:
University of Notre Dame, Institute for Flow Physics and Control, Aerospace and Mechanical Engineering Department, Notre Dame, IN 46556, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This research investigates the effect of uniform suction on the absolute instability of Type I cross-flow modes in the boundary layer on a rotating disk. Specifically, it is designed to investigate whether wall suction would transform the absolute instability into a global mode, as first postulated in the numerical simulations of Davies & Carpenter (J. Fluid Mech., vol. 486, 2003, pp. 287–329). The disk is designed so that with a suction parameter of 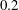$0.2$, the radial location of the absolute instability critical Reynolds number, 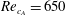$Re_{c_{A}}=650$, occurs on the disk. Wall suction is applied from 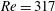$Re=317$ to 696.5. The design for wall suction follows that of Gregory & Walker (J. Fluid Mech., 1960, pp. 225–234) where an array of holes through the disk communicate between the measurement side of the disk and the underside of the disk which is inside of an enclosure that is maintained at a slight vacuum. The enclosure pressure is adjustable so that a range of suction or blowing parameters can be investigated. The holes in the measurement surface are covered by a compressed wire porous mesh to aid in uniformizing the suction on the measurement surface of the disk. The mesh is covered by a thin porous high-density polyethylene sheet featuring a 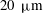$20~{\rm\mu}\text{m}$ pore size which provides a smooth finely porous surface. A companion numerical simulation is performed to investigate the effect that the size and vacuum pressure of the underside enclosure have on the uniformity of the measurement surface suction. Temporal disturbances are introduced using the method of Othman & Corke (J. Fluid Mech., 2006, pp. 63–94). The results document the evolution of disturbance wavepackets in space and time. These show a temporal growth of the wavepackets as the location of the absolute instability is approached which is in strong contrast to the temporal evolution without suction observed by Othman and Corke. The results appear to support the effect of wall suction on the absolute instability postulated by Thomas (PhD thesis, 2007, Cardiff University, UK) and Thomas & Davies (J. Fluid Mech., vol. 663, 2010, pp. 401–433).

JFM classification

Instability: Absolute/convective instability Boundary Layers: Boundary layer stability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 704 - 737
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, H. C. 1970 Computer Techniques in Image Processing. Academic.Google Scholar
Appelquist, E., Schlatter, P., Alfredsson, P. H. & Lingwood, R. J. 2015 Global linear instability of the rotating-disk flow investigated through simulations. J. Fluid Mech. 765, 612–631.CrossRefGoogle Scholar
Corke, T., Matlis, E. & Othman, H. 2007 Transition to turbulence in rotating-disk boundary layers – convective and absolute instabilities. J. Engng Maths 57, 253–272.Google Scholar
Corke, T. C. & Knasiak, K. F. 1998 Stationary travelling cross-flow mode interactions on a rotating disk. J. Fluid Mech. 355, 285–315.Google Scholar
Corke, T. C. & Matlis, E. H. 2006 Transition to turbulence in 3D boundary layers on a rotating disk – triad resonance. In IUTAM Symposium on 100 Years Boundary Layer Research, pp. 189–199. Springer.Google Scholar
Davies, C. & Carpenter, P. W. 2001 A novel velocity–vorticity formulation of Navier–Stokes equations with applications to boundary layer disturbance evolution. J. Comput. Phys. 172 (1), 119–165.Google Scholar
Davies, C. & Carpenter, P. W. 2003 Global behaviour corresponding to the absolute instability of the rotating disk boundary layer. J. Fluid Mech. 486, 287–329.Google Scholar
Davies, C., Thomas, C. & Carpenter, P. W. 2007 Global stability of the rotating-disk boundary layer. J. Engng Maths 57, 219–236.Google Scholar
Dhanak, M. R. 1992 Effects on uniform suction on the stability of flow on a rotating disk. Proc. R. Soc. Lond. 439, 431–440.Google Scholar
Faller, A.J. 1991 Instability and transition of disturbed flow over a rotating disk. J. Fluid Mech. 230, 245–269.Google Scholar
Gregory, N., Stuart, J. T. & Walker, W. S. 1955 On the stability of three-dimensional boundary layers with application to the flow due to a rotating disk. Phil. Trans. R. Soc. Lond. 248, 155–199.Google Scholar
Gregory, N. & Walker, W. S. 1953 Experiments on the flow due to a rotating disc. Fluid Motion Sub-Committee; A.R.C. 16, Sept. 22.Google Scholar
Gregory, N. & Walker, W. S. 1960 Experiments on the effect of suction on the flow due to a rotating disk. J. Fluid Mech. 9, 225–234.Google Scholar
Healey, J. J. 2010 Model for unstable global modes in the rotating-disk boundary layer. J. Fluid Mech. 663, 148–159.Google Scholar
Herbert, T. 1990 A code for linear stability analysis. In Instabilities and Transition (ed. Hussaini, M. Y. & Voight, R. G.), pp. 121–144. Springer.Google Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2013 An experimental study of edge effects on rotating-disk transition. J. Fluid Mech. 716, 638–657.CrossRefGoogle Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2014 On the laminar–turbulent transition of the rotating disk flow: role of absolute instability. J. Fluid Mech. 745, 132–163.Google Scholar
Kohama, Y., Kobayashi, R. & Takamadate, C. 1980 Spiral vortices in boundary layer transition regime on a rotating disk. Acta Mech. 35, 71–82.Google Scholar
Lingwood, R. J. 1995 Absolute instability of the boundary layer on a rotating disk. J. Fluid Mech. 314, 373–405.Google Scholar
Lingwood, R. J. 1996 An experimental study of absolute instability of the rotating-disk boundary-layer flow. J. Fluid Mech. 314, 373–405.Google Scholar
Lingwood, R. J. 1997 On the effects of suction and injection on the absolute instability of the rotating-disk boundary layer. Phys. Fluids 9, 1317–1328.Google Scholar
Malik, M. R., Wilkinson, S. P. & Orzag, S. A. 1981 Instability and transition in rotating disk flow. AIAA J. 19, 1131–1138.CrossRefGoogle Scholar
Othman, H. & Corke, T. C. 2006 Experimental investigation of absolute instability of a rotating-disk boundary layer. J. Fluid Mech. 565, 63–94.Google Scholar
Pier, B. 2003 Finite-amplitude crossflow vortices, secondary instability, and transition in the rotating-disk boundary layer. J. Fluid Mech. 487, 315–343.Google Scholar
Pier, B. 2013 Transition near the edge of a rotating disk. J. Fluid Mech. 737, R1–R9.Google Scholar
Schlichting, H. 1968 Boundary-Layer Theory, 6th edn. McGraw-Hill.Google Scholar
Siddiqui, M., Mukund, V., Scott, J. & Pier, B. 2013 Experimental characterization of transition region in rotating-disk boundary layer. Phys. Fluids 25, 034102,1–10.Google Scholar
Smith, N. H. 1946 Exploratory investigation of laminar boundary layer oscillations on a rotating disk. Technical Note NACA TN-1227.Google Scholar
Stuart, J. T. 1954 On the effects of uniform suction on steady flow due to a rotating disk. Q. J. Mech. Appl. Maths VII, 446–457.CrossRefGoogle Scholar
Thomas, C.2007 Numerical simulations of disturbance development in rotating boundary layers. PhD thesis, Cardiff University, UK.Google Scholar
Thomas, C. & Davies, C. 2010 The effects of mass transfer on the global stability of the rotating-disk boundary layer. J. Fluid Mech. 663, 401–433.Google Scholar
Thomas, J. B. 1965 An Introduction to Statistical Communication Theory. Wiley.Google Scholar
Turin, G. L. 1960 An introduction to matched filters. IRE Trans. Inf. Theory IT‐6 (3), 311–329.Google Scholar
Wilkinson, S. P. & Malik, M. R. 1985 Stability experiments in the flow over a rotating disk. AIAA J. 23, 588–595.Google Scholar
Wilkinson, S. P., Malik, M. R. & Orzag, S. A. 1981 Instability and transition in rotating disk flow. AIAA J. 4, 1131–1138.Google Scholar