Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T13:29:26.245Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of turbulent fluctuations on the drag and lift forces on a towed sphere and its boundary layer

Published online by Cambridge University Press:  13 March 2013

Holger Homann ,
Jérémie Bec  and
Rainer Grauer
Holger Homann*
Affiliation:
Laboratoire J.-L. Lagrange UMR 7293, Université de Nice-Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur, BP4228, 06304 Nice, France
Jérémie Bec
Affiliation:
Laboratoire J.-L. Lagrange UMR 7293, Université de Nice-Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur, BP4228, 06304 Nice, France
Rainer Grauer
Affiliation:
Theoretische Physik I, Ruhr-Universität, 44780 Bochum, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The impact of turbulent fluctuations on the forces exerted by a fluid on a towed spherical particle is investigated by means of high-resolution direct numerical simulations. The measurements are carried out using a novel scheme to integrate the two-way coupling between the particle and the incompressible surrounding fluid flow maintained in a high-Reynolds-number turbulent regime. The main idea consists of combining a Fourier pseudo-spectral method for the fluid with an immersed-boundary technique to impose the no-slip boundary condition on the surface of the particle. This scheme is shown to converge as the power 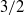$3/ 2$ of the spatial resolution. This behaviour is explained by the 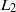${L}_{2} $ convergence of the Fourier representation of a velocity field displaying discontinuities of its derivative. Benchmarking of the code is performed by measuring the drag and lift coefficients and the torque-free rotation rate of a spherical particle in various configurations of an upstream-laminar carrier flow. Such studies show a good agreement with experimental and numerical measurements from other groups. A study of the turbulent wake downstream of the sphere is also reported. The mean velocity deficit is shown to behave as the inverse of the distance from the particle, as predicted from classical similarity analysis. This law is reinterpreted in terms of the principle of ‘permanence of large eddies’ that relates infrared asymptotic self-similarity to the law of decay of energy in homogeneous turbulence. The developed method is then used to attack the problem of an upstream flow that is in a developed turbulent regime. It is shown that the average drag force increases as a function of the turbulent intensity and the particle Reynolds number. This increase is significantly larger than predicted by standard drag correlations based on laminar upstream flows. It is found that the relevant parameter is the ratio of the viscous boundary layer thickness to the dissipation scale of the ambient turbulent flow. The drag enhancement can be motivated by the modification of the mean velocity and pressure profile around the sphere by small-scale turbulent fluctuations. It is demonstrated that the variance of the drag force fluctuations can be modelled by means of standard drag correlations. Temporal correlations of the drag and lift forces are also presented.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulence simulation Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 721 , 25 April 2013 , pp. 155 - 179
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amoura, Z., Roig, V., Risso, F. & Billet, A.-M. 2010 Attenuation of the wake of a sphere in an intense incident turbulence with large length scales. Phys. Fluids 22, 055105.CrossRefGoogle Scholar
Anderson, Uhlherr 1977 The influence of stream turbulence on the drag of freely endtrained spheres. In 6th Australasian Hydraulics and Fluid Mechanics Conference Adelaide, Australia, 5–9 December 1977, pp. 541–545.Google Scholar
Angot, P., Bruneau, C. H. & Fabrie, P. 1999 A penalization method to take into account obstacles in incompressible viscous flows. Numer. Math. 81 (4), 497–520.CrossRefGoogle Scholar
Bagchi, P. & Balachandar, S. 2002 Effect of free rotation on the motion of a solid sphere in linear shear flow at moderate Re. Phys. Fluids 14, 2719–2737.Google Scholar
Bagchi, P. & Balachandar, S. 2003 Effect of turbulence on the drag and lift of a particle. Phys. Fluids 15 (11), 3496.Google Scholar
Bagchi, P. & Balachandar, S. 2004 Response of the wake of an isolated particle to an isotropic turbulent flow. J. Fluid Mech. 518, 95–123.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42 (1), 111–133.Google Scholar
Brown, D. L., Cortez, R. & Minion, M. L. 2001 Accurate projection methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 168 (2), 464–499.Google Scholar
Brucato, A, Grisafi, F & Montante, G 1998 Particle drag coefficients in turbulent fluids. Chem. Engng Sci. 53 (18), 3295–3314.CrossRefGoogle Scholar
Burton, T. & Eaton, J. K. 2005 Fully resolved simulations of particle–turbulence interaction. J. Fluid Mech. 545, 67–111.CrossRefGoogle Scholar
Calzavarini, E., Volk, R., Bourgoin, M., Leveque, E., Pinton, J. F. & Toschi, F. 2009 Acceleration statistics of finite-sized particles in turbulent flow: the role of Faxén forces. J. Fluid Mech. 630, 179–190.Google Scholar
Calzavarini, E., Volk, R., Lévqˆue, E., Pinton, J. F. & Toschi, F. 2012 Impact of trailing wake drag on the statistical properties and dynamics of finite-sized particle in turbulence. Physica D 241 (3), 237–244.CrossRefGoogle Scholar
Dandy, D. S. & Dwyer, H. A. 1990 A sphere in shear flow at finite Reynolds number: effect of shear on particle lift, drag, and heat transfer. J. Fluid Mech. 216, 381–410.Google Scholar
Eames, I., Johnson, P. B., Roig, V. & Risso, F. 2011 Effect of turbulence on the downstream velocity deficit of a rigid sphere. Phys. Fluids 23, 095103.CrossRefGoogle Scholar
Fadlun, E. A., Verzicco, R., Orlandi, P. & Mohd-Yusof, J. 2000 Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 60, 35–60.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence. Cambridge University Press.CrossRefGoogle Scholar
Goldstein, D., Handler, R. & Sirovich, L. 1993 Modelling a no-slip flow boundary with an external force field. J. Comp. Phys. 105, 354–366.CrossRefGoogle Scholar
Homann, H. & Bec, J. 2010 Finite-size effects in the dynamics of neutrally buoyant particles in turbulent flow. J. Fluid Mech. 651, 81–91.Google Scholar
Kim, J. & Balachandar, S. 2012 Mean and fluctuating components of drag and lift forces on an isolated finite-sized particle in turbulence. Theor. Comput. Fluid Dyn. 26 (1), 185–204.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 Energy dissipation in locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 19–21.Google Scholar
Kurose, R. & Komori, S. 1999 Drag and lift forces on a rotating sphere in a linear shear flow. J. Fluid Mech. 384, 183–206.CrossRefGoogle Scholar
Le Clair, B. P., Hamielec, A. E. & Pruppacher, H. R. 1970 A numerical study of the drag on a sphere at low and intermediate Reynolds numbers. J. Atmos. Sci. 27, 308–315.Google Scholar
Lin, C. J., Peery, J. H. & Showalter, W. R. 1970 Simple shear flow round inertial effects and suspension rheology. J. Fluid Mech. 44, 1–17.CrossRefGoogle Scholar
Luo, K., Wang, Z. & Fan, J. 2010 Response of force behaviours of a spherical particle to an oscillating flow. Phys. Lett. A 374 (30), 3046–3052.CrossRefGoogle Scholar
Merle, A., Legendre, D. & Magnaudet, J. 2005 Forces on a high-Reynolds-number spherical bubble in a turbulent flow. J. Fluid Mech. 532, 53–62.CrossRefGoogle Scholar
Mohd-Yusof, J. 1997 Combined immersed boundary/b-spline methods for simulations of flow in complex geometries. Center for Turbulence Research – Annual Research Briefs pp. 317–327.Google Scholar
Naso, A. & Prosperetti, A. 2010 The interaction between a solid particle and a turbulent flow. New J. Phys. 12 (3), 033040.Google Scholar
Pasquetti, R., Bwemba, R. & Cousin, L. 2008 A pseudo-penalization method for high Reynolds number unsteady flows. Appl. Numer. Math. 58 (7), 946–954.CrossRefGoogle Scholar
de Pater, I. & Lissauer, J. 2001 Planetary Science. Cambridge University Press.Google Scholar
Patterson, G. S. & Orszag, S. A. 1971 Spectral calculation of isotropic turbulence: efficient removal of aliasing interaction. Phys. Fluids 14, 2538–2541.CrossRefGoogle Scholar
Peskin, C. S. 1977 Numerical analysis of blood flow in the heart. J. Comput. Phys. 25, 220–252.Google Scholar
Pope, S. B. 2000 Turbulent Flows, 1st edn. Cambridge University Press.Google Scholar
Prosperetti, A. & Oguz, H. N. 2001 Physalis: a new o(N) method for the numerical simulation of disperse systems: potential flow of spheres. J. Comput. Phys. 167 (1), 196–216.CrossRefGoogle Scholar
Qureshi, N. M., Bourgoin, M., Baudet, C., Cartellier, A. & Gagne, Y. 2007 Turbulent transport of material particles: an experimental study of finite size effects. Phys. Rev. Lett. 99 (18), 184502.Google Scholar
Schiller, L. & Naumann, A. 1933 Über die grundlegenden berechnungen bei der schwerkraftaufbereitung. Verein. Deutsch. Ing. 77, 318–320.Google Scholar
Schlichting, H. 1979 Boundary-Layer Theory. McGraw-Hill.Google Scholar
Seinfeld, J. H. & Pandis, S. N. 1998 From Air Pollution to Climate Change. John Wiley and Sons.Google Scholar
Shaw, R. A. 2003 Particle–turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35 (1), 183–227.Google Scholar
Shu, C. & Osher, S. 1988 Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77, 439–471.Google Scholar
Taira, K. & Colonius, T. 2007 The immersed boundary method: a projection approach. J. Comput. Phys. 225 (2), 2118–2137.Google Scholar
Uberoi, M. S. & Freymuth, P. 1970 Turbulent energy balance and spectra of the axisymmetric wake. Phys. Fluids 13, 2205–2210.CrossRefGoogle Scholar
Uhlmann, M. 2005 An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209 (2), 448–476.CrossRefGoogle Scholar
Volk, R., Calzavarini, E., Lévêque, E. & Pinton, J.-F. 2011 Dynamics of inertial particles in a turbulent von Kármán flow. J. Fluid Mech. 668, 223–235.Google Scholar
Warnica, W. D., Renksizbulut, M. & Strong, A. B. 1995 Drag coefficients of spherical liquid droplets. Part 2: Turbulent gaseous fields. Exp. Fluids 18 (4), 265–276.Google Scholar
Wu, J.-S. & Faeth, G. M. 1994 Sphere wakes at moderate Reynolds numbers in a turbulent environment. AIAA J. 32 (3), 535–541.Google Scholar
Xu, H. & Bodenschatz, E. 2008 Motion of inertial particles with size larger than Kolmogorov scale in turbulent flows. Physica D: Nonlinear Phenomena 237 (14–17), 2095–2100.CrossRefGoogle Scholar
Yeo, K., Dong, S., Climent, E. & Maxey, M. R. 2010 Modulation of homogeneous turbulence seeded with finite size bubbles or particles. Intl J. Multiphase Flow 36 (3), 221–233.Google Scholar