Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Italia, Matteo
Croccolo, Fabrizio
Scheffold, Frank
and
Vailati, Alberto
2014.
Inclined layer convection in a colloidal suspension with negative Soret coefficient at large solutal Rayleigh numbers.
The European Physical Journal E,
Vol. 37,
Issue. 10,
Qiang, Wei
and
Cao, Hui
2014.
Flow patterns in inclined-layer turbulent convection.
The European Physical Journal E,
Vol. 37,
Issue. 7,
Huisman, Sander G.
van der Veen, Roeland C.A.
Sun, Chao
and
Lohse, Detlef
2014.
Multiple states in highly turbulent Taylor–Couette flow.
Nature Communications,
Vol. 5,
Issue. 1,
Frick, P.
Khalilov, R.
Kolesnichenko, I.
Mamykin, A.
Pakholkov, V.
Pavlinov, A.
and
Rogozhkin, S.
2015.
Turbulent convective heat transfer in a long cylinder with liquid sodium.
EPL (Europhysics Letters),
Vol. 109,
Issue. 1,
p.
14002.
Guo, Shuang-Xi
Zhou, Sheng-Qi
Cen, Xian-Rong
Qu, Ling
Lu, Yuan-Zheng
Sun, Liang
and
Shang, Xiao-Dong
2015.
The effect of cell tilting on turbulent thermal convection in a rectangular cell.
Journal of Fluid Mechanics,
Vol. 762,
Issue. ,
p.
273.
Shishkina, Olga
and
Horn, Susanne
2016.
Thermal convection in inclined cylindrical containers.
Journal of Fluid Mechanics,
Vol. 790,
Issue. ,
van der Veen, Roeland C. A.
Huisman, Sander G.
Dung, On-Yu
Tang, Ho L.
Sun, Chao
and
Lohse, Detlef
2016.
Exploring the phase space of multiple states in highly turbulent Taylor-Couette flow.
Physical Review Fluids,
Vol. 1,
Issue. 2,
Xi, Heng-Dong
Zhang, Yi-Bao
Hao, Jian-Tao
and
Xia, Ke-Qing
2016.
Higher-order flow modes in turbulent Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 805,
Issue. ,
p.
31.
Wei, Ping
and
Ahlers, Guenter
2016.
On the nature of fluctuations in turbulent Rayleigh–Bénard convection at large Prandtl numbers.
Journal of Fluid Mechanics,
Vol. 802,
Issue. ,
p.
203.
Teimurazov, Andrei
and
Frick, Peter
2017.
Thermal convection of liquid metal in a long inclined cylinder.
Physical Review Fluids,
Vol. 2,
Issue. 11,
Guo, Shuang-Xi
Zhou, Sheng-Qi
Qu, Ling
Cen, Xian-Rong
and
Lu, Yuan-Zheng
2017.
Evolution and statistics of thermal plumes in tilted turbulent convection.
International Journal of Heat and Mass Transfer,
Vol. 111,
Issue. ,
p.
933.
Kouloulias, K.
Sergis, A.
Hardalupas, Y.
and
Barrett, T.R.
2017.
Measurement of flow velocity during turbulent natural convection in nanofluids.
Fusion Engineering and Design,
Vol. 123,
Issue. ,
p.
72.
Qiang, Wei
Cao, Hui
Li, Weimin
and
Zhang, Fansiqi
2017.
Counter-gradient heat transport by large-scale circulation in two-dimensional turbulent convection.
EPL (Europhysics Letters),
Vol. 118,
Issue. 6,
p.
64001.
Wang, Qi
Wan, Zhen-Hua
Yan, Rui
and
Sun, De-Jun
2018.
Multiple states and heat transfer in two-dimensional tilted convection with large aspect ratios.
Physical Review Fluids,
Vol. 3,
Issue. 11,
Xia, Zhenhua
Shi, Yipeng
Cai, Qingdong
Wan, Minping
and
Chen, Shiyi
2018.
Multiple states in turbulent plane Couette flow with spanwise rotation.
Journal of Fluid Mechanics,
Vol. 837,
Issue. ,
p.
477.
Zwirner, Lukas
and
Shishkina, Olga
2018.
Confined inclined thermal convection in low-Prandtl-number fluids.
Journal of Fluid Mechanics,
Vol. 850,
Issue. ,
p.
984.
Khalilov, Ruslan
Kolesnichenko, Ilya
Pavlinov, Alexander
Mamykin, Andrey
Shestakov, Alexander
and
Frick, Peter
2018.
Thermal convection of liquid sodium in inclined cylinders.
Physical Review Fluids,
Vol. 3,
Issue. 4,
Xia, Zhenhua
Shi, Yipeng
Wan, Minping
Sun, Chao
Cai, Qingdong
and
Chen, Shiyi
2019.
Role of the large-scale structures in spanwise rotating plane Couette flow with multiple states.
Physical Review Fluids,
Vol. 4,
Issue. 10,
Wang, Qi
Wan, Zhen-Hua
Yan, Rui
and
Sun, De-Jun
2019.
Flow organization and heat transfer in two-dimensional tilted convection with aspect ratio 0.5.
Physics of Fluids,
Vol. 31,
Issue. 2,
Kouloulias, K.
Sergis, A.
and
Hardalupas, Y.
2019.
Assessing the flow characteristics of nanofluids during turbulent natural convection.
Journal of Thermal Analysis and Calorimetry,
Vol. 135,
Issue. 6,
p.
3181.
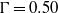 $\Gamma = 0. 50$
$\Gamma = 0. 50$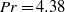 $\mathit{Pr}= 4. 38$ in a cylindrical cell with an aspect ratio
$\mathit{Pr}= 4. 38$ in a cylindrical cell with an aspect ratio  $\Gamma = 0. 50$. The rotational symmetry was broken by a small tilt of the sample axis relative to gravity. Measurements of the heat transport (as expressed by the Nusselt number Nu), as well as properties of the large-scale circulation (LSC) obtained from temperature measurements along the sidewall, are presented. In contradistinction to similar experiments using containers of aspect ratio
$\Gamma = 0. 50$. The rotational symmetry was broken by a small tilt of the sample axis relative to gravity. Measurements of the heat transport (as expressed by the Nusselt number Nu), as well as properties of the large-scale circulation (LSC) obtained from temperature measurements along the sidewall, are presented. In contradistinction to similar experiments using containers of aspect ratio  $\Gamma = 1. 00$ (Ahlers et al., J. Fluid Mech., vol. 557, 2006b, pp. 347–367) and
$\Gamma = 1. 00$ (Ahlers et al., J. Fluid Mech., vol. 557, 2006b, pp. 347–367) and 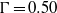 $\Gamma = 0. 50$ (Chillà et al., Eur. Phys. J. B, vol. 40, 2004, pp. 223–227; Sun, Xi & Xia, Phys. Rev. Lett., vol. 95, 2005, p. 074502; Roche et al., New J. Phys., vol. 12, 2010, p. 085014), we see a very small increase of the heat transport for tilt angles up to about 0.1 rad. Based on measurements of properties of the LSC we explain this increase by a stabilization of the single-roll state (SRS) of the LSC and a destabilization of the double-roll state (DRS) (it is known from previous work that the SRS has a slightly larger heat transport than the DRS). Quantitative measurements of the strength and the orientation of the LSC show that its azimuthal diffusion is suppressed with increasing tilt whereas the torsional oscillation becomes more pronounced and its frequency increases.
$\Gamma = 0. 50$ (Chillà et al., Eur. Phys. J. B, vol. 40, 2004, pp. 223–227; Sun, Xi & Xia, Phys. Rev. Lett., vol. 95, 2005, p. 074502; Roche et al., New J. Phys., vol. 12, 2010, p. 085014), we see a very small increase of the heat transport for tilt angles up to about 0.1 rad. Based on measurements of properties of the LSC we explain this increase by a stabilization of the single-roll state (SRS) of the LSC and a destabilization of the double-roll state (DRS) (it is known from previous work that the SRS has a slightly larger heat transport than the DRS). Quantitative measurements of the strength and the orientation of the LSC show that its azimuthal diffusion is suppressed with increasing tilt whereas the torsional oscillation becomes more pronounced and its frequency increases.