Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lacassagne, T.
Simoëns, S.
EL Hajem, M.
Lyon, A.
and
Champagne, J.-Y.
2019.
Oscillating grid turbulence in shear-thinning polymer solutions.
Physics of Fluids,
Vol. 31,
Issue. 8,
Kim, Jee Young
Morisada, Shintaro
Kawakita, Hidetaka
and
Ohto, Keisuke
2019.
Solvent extraction kinetics of Ag(I) with methyl ketonic p-tert-octylcalix[4]arene in the modified Lewis cell technique.
Journal of Inclusion Phenomena and Macrocyclic Chemistry,
Vol. 94,
Issue. 3-4,
p.
219.
Herlina, H.
and
Wissink, J. G.
2019.
Simulation of air–water interfacial mass transfer driven by high-intensity isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 860,
Issue. ,
p.
419.
Sanjou, M.
2020.
Local gas transfer rate through the free surface in spatially accelerated open-channel turbulence.
Physics of Fluids,
Vol. 32,
Issue. 10,
Lacassagne, T.
Simoëns, S.
EL Hajem, M.
and
Champagne, J.-Y.
2020.
Oscillating grid generating turbulence near gas-liquid interfaces in shear-thinning dilute polymer solutions.
Physical Review Fluids,
Vol. 5,
Issue. 3,
de Souza Lopes Silva, Pedro
Mateus, Marcos Vinícius
Ferreira, Deusmaque Carneiro
da Luz, Mário Sérgio
Araújo Naves, Emiliane Andrade
Martins, Mário Machado
Goulart, Luiz Ricardo
Cunha, Luís Carlos Scalon
and
de Souza Inácio Gonçalves, Julio Cesar
2020.
Humic substances reduce the oxygen mass transfer in the air–water interface.
AIChE Journal,
Vol. 66,
Issue. 6,
Saritha, K.
Gandhimathi , T.
and
Rameshkumar, M.
2020.
Mass transfer phenomena of MHD nanofluid with chemical reaction with base fluids water and kerosene.
Malaya Journal of Matematik,
Vol. 8,
Issue. 2,
p.
668.
Ermers, J.
Kottapalli, S.
Waterson, N.P.
Smeulders, D.M.J.
and
Nakiboglu, G.
2021.
A predictive model for dissolution of stably trapped bubbles in corner cavities.
International Journal of Heat and Mass Transfer,
Vol. 179,
Issue. ,
p.
121703.
Pinelli, Michele
Herlina, H.
Wissink, J.G.
and
Uhlmann, M.
2022.
Direct numerical simulation of turbulent mass transfer at the surface of an open channel flow.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Dani, Adil
Cockx, Arnaud
Legendre, Dominique
and
Guiraud, Pascal
2022.
Effect of spheroid bubble interface contamination on gas-liquid mass transfer at intermediate Reynolds numbers: From DNS to Sherwood numbers.
Chemical Engineering Science,
Vol. 248,
Issue. ,
p.
116979.
Lacassagne, Tom
EL Hajem, Mahmoud
Champagne, Jean-Yves
and
Simoëns, Serge
2022.
Turbulent mass transfer near gas-liquid interfaces in water and shear-thinning dilute polymer solution.
International Journal of Heat and Mass Transfer,
Vol. 194,
Issue. ,
p.
122975.
Zudin, Yuri B.
2023.
Theory of Periodic Conjugate Heat Transfer.
p.
281.
Wissink, Jan G.
and
Herlina, H.
2023.
Surface-temperature-induced Marangoni effects on developing buoyancy-driven flow.
Journal of Fluid Mechanics,
Vol. 962,
Issue. ,
Fu, Ye
Hao, Hua
Liu, Yiren
Fu, Shuai
Guo, Qinghu
Wang, Zhen
Li, Dongxu
Cao, Minghe
Yao, Zhonghua
and
Liu, Hanxing
2024.
Synergistic improved piezocatalytic performance of surface group functioned and heterovalently doped barium titanate nanoparticles.
Journal of Materials Science: Materials in Electronics,
Vol. 35,
Issue. 13,
Wissink, Jan
Ali, Fatima
and
Herlina, Herlina
2025.
Proceedings of the Cambridge Unsteady Flow Symposium 2024.
p.
243.
Qi, Yinghe
Li, Yaxing
and
Coletti, Filippo
2025.
Small-scale dynamics and structure of free-surface turbulence.
Journal of Fluid Mechanics,
Vol. 1007,
Issue. ,
Jamin, Timothée
Berhanu, Michael
and
Falcon, Eric
2025.
Experimental study of three-dimensional turbulence under a free surface.
Physical Review Fluids,
Vol. 10,
Issue. 3,
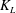 $K_{L}$ is found to scale as a power of the Schmidt number, i.e.
$K_{L}$ is found to scale as a power of the Schmidt number, i.e. 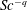 $Sc^{-q}$, where
$Sc^{-q}$, where 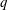 $q$ smoothly transitions from
$q$ smoothly transitions from 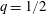 $q=1/2$ for clean surfaces to
$q=1/2$ for clean surfaces to 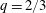 $q=2/3$ for very dirty interfaces. A power law
$q=2/3$ for very dirty interfaces. A power law 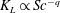 $K_{L}\propto Sc^{-q}$ is proposed in which both the exponent
$K_{L}\propto Sc^{-q}$ is proposed in which both the exponent 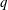 $q$ and the constant of proportionality become functions of the clean surface fraction.
$q$ and the constant of proportionality become functions of the clean surface fraction.